Министерство образования Российской Федерации

Филиал Северного Арктического Федерального Университета

Севмашвтуз

Кафедра математики

Черткова Ольга Владимировна

Методические указания

К выполнению контрольной работы №4 по “Линейной алгебре ” для заочного обучения

1.Методические указания к контрольной работе №4

по теме «Матрица линейного оператора»

1.1. Задание №1

Для решения задания студент должен знать закон изменения матрицы линейного оператора при переходе от базиса к базису, определение сопряженного оператора и его свойства.

Теорема №3. Матрица линейного оператора А при переходе от базиса е_i к базису е_i^/ изменяется по формуле: , где - матрица перехода между базисами е_i и е_i^/.

Определение №11. Oператор A^*, действующий из V в V, называется сопряженным к оператору A, если для любых х,у выполняется

(Ах, у)=(х, A^*у).

В ортонормированном базисе матрицы оператор А и оператор А^* связаны соотношением А^*=А^Т.

Пример №6. Найти матрицу линейного оператора А в базисе е_i^/, если он задан своей матрицей в базисе е_i : A=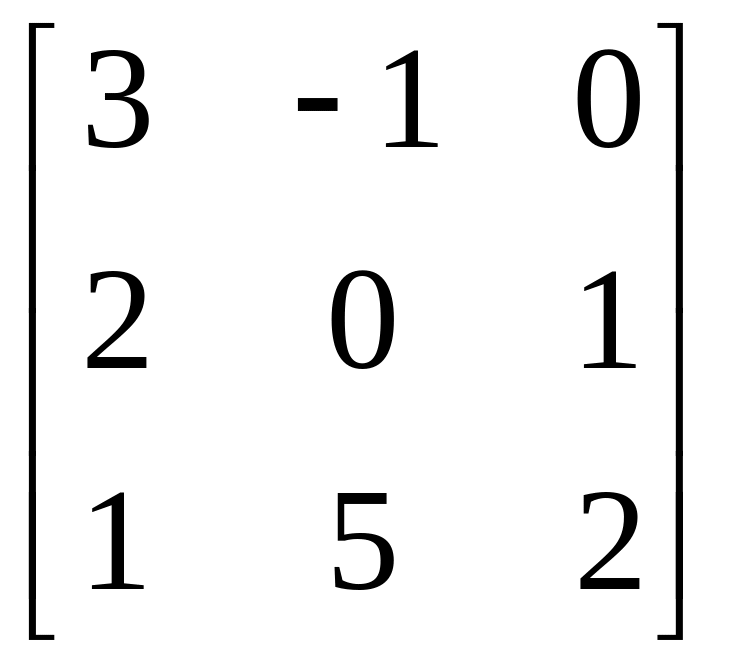 и

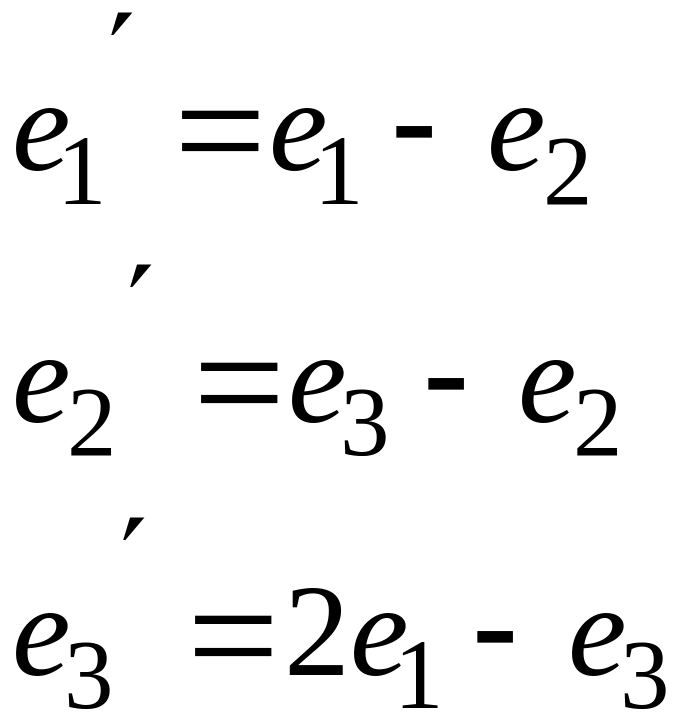
Решение: Матрица перехода между базисами:

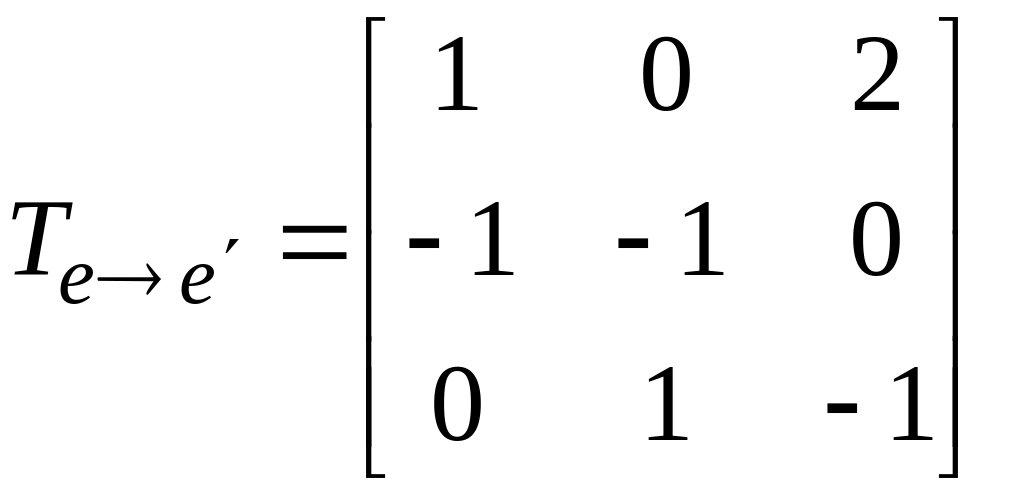
detT=1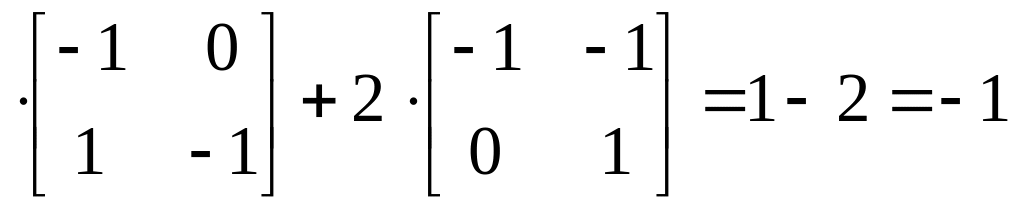

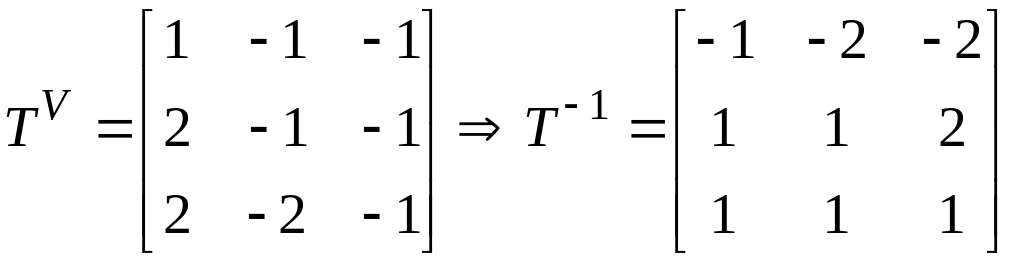
Воспользуемся формулой :

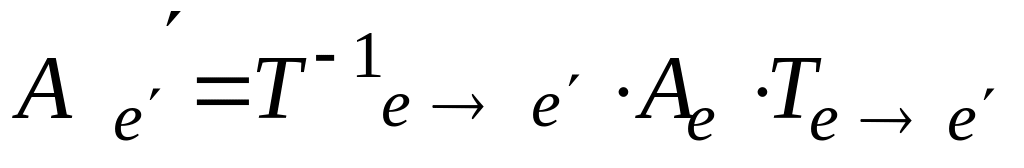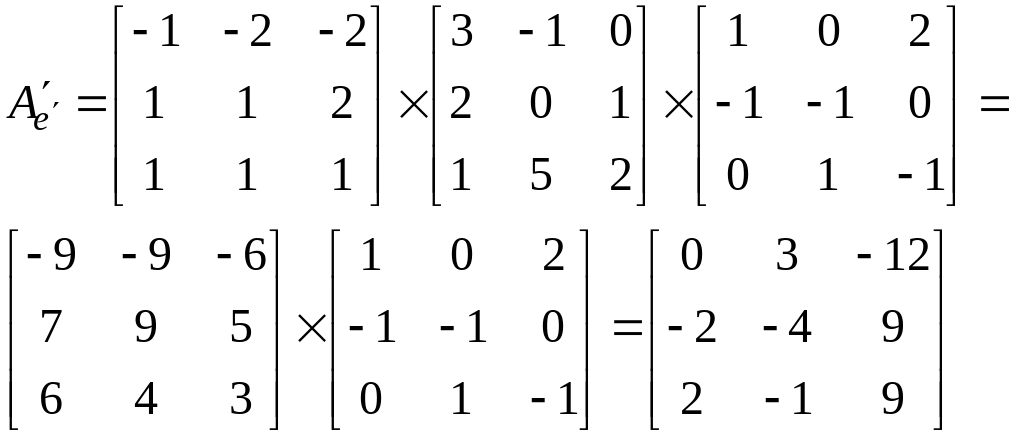
Ответ: .

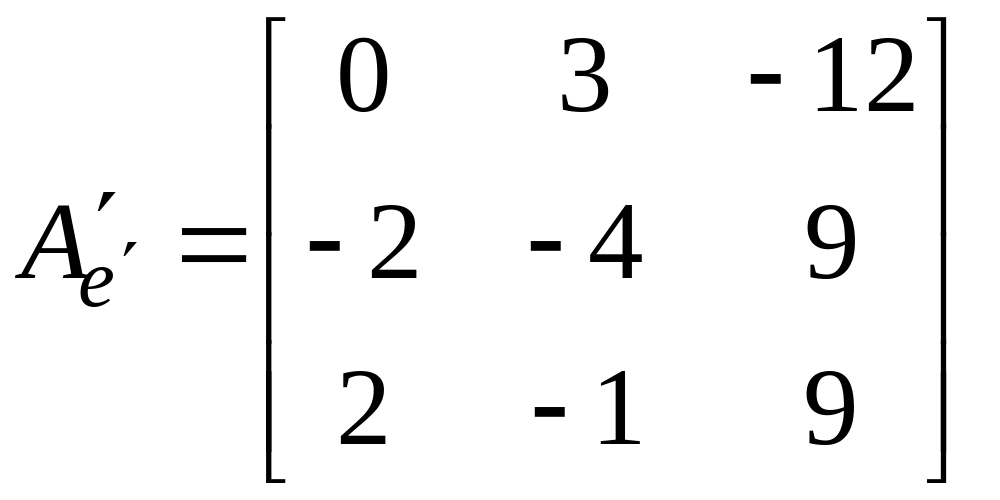1.2 Задание №2

При выполнении данного задания студент должен владеть навыками нахождения собственных чисел и векторов, приведения матрицы линейного оператора к диагональному виду .

Определение №12. Ненулевой элемент х называется собственным вектором оператора А, если оператор А переводит элемент х в элемент λх, т.е. Ах= λх. При этом λ называется собственным значением или числом оператора, соответствующим собственному вектору х.

Например, оператор А, заданный матрицей A= имеет собственный вектор Х= , отвечающий собственному значению λ=4:

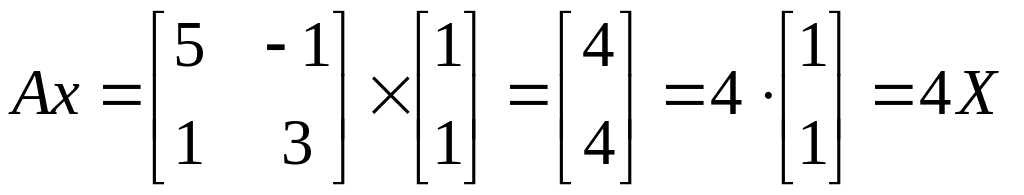
Определение №13. Многочлен относительно λ: det(A-λE) называется характеристическим многочленом оператора А.

Уравнение det(A-λE) = 0 – называется характеристическим уравнением оператора А.

Например, det(A-λE)=det( λ ) = det( - )= det =(5-λ)(3-λ)+1=15-3λ-5λ+λ²+1=λ²-8λ+16- характеристи-ческий многочлен оператора А.

Собственные вектора обладают следующими свойствами:

Теорема № 4. Отвечающие различным собственным значениям λ₁, λ₂, …λ_p собственные вектора е₁, е₂, …е_p – линейно независимы.

Теорема №5. Для того чтобы матрица А линейного оператора А в данном базисе е₁…е_n была диагональной, необходимо и достаточно, чтобы базисные векторы е₁…е_n были собственными векторами оператора А.

Теорема №6. Для того чтобы λ было собственным значением оператора, необходимо и достаточно, чтобы λ было корнем характеристического уравнения оператора А.

Таким образом, чтобы решить задачу о собственных значениях и векторах линейного оператора, необходимо решить характеристическое уравнение det(A- E)=0 и подставить его корни в условие , которое эквивалентно системе (A-- E)X=0 .

Пример №7. Привести матрицу линейного оператора А к диагональному виду и указать базис. A =

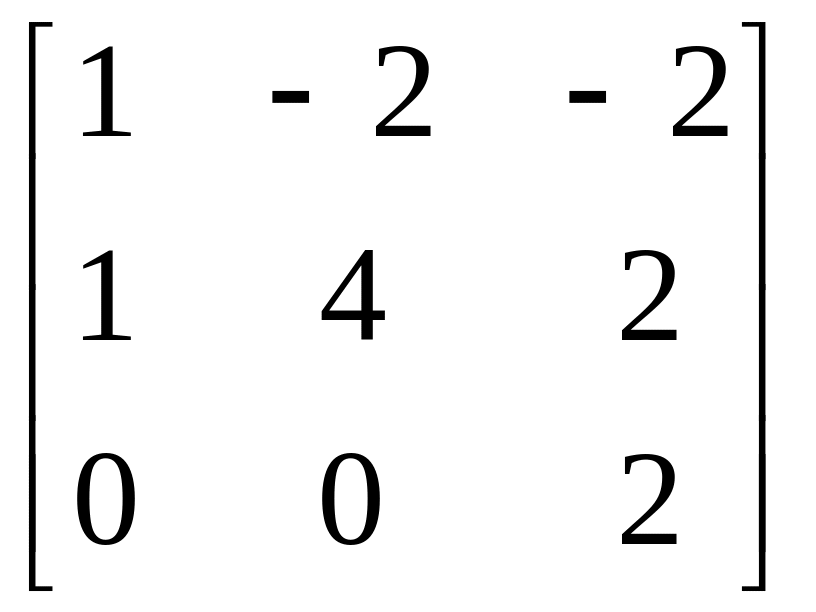
Решение: составим характеристическое уравнение

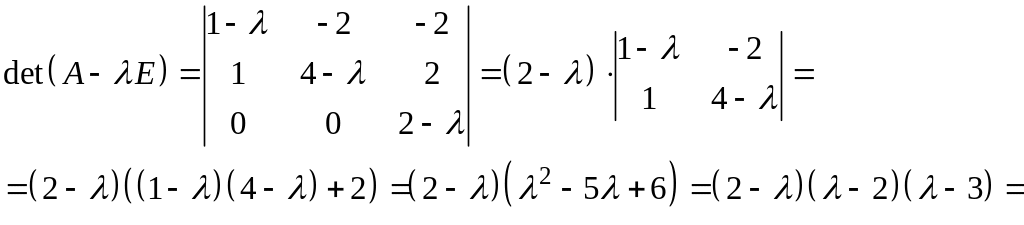
Т.о. и - собственные значения оператора А. Найдем собственные векторы из условия (A - E)X=0

При λ₁=2:

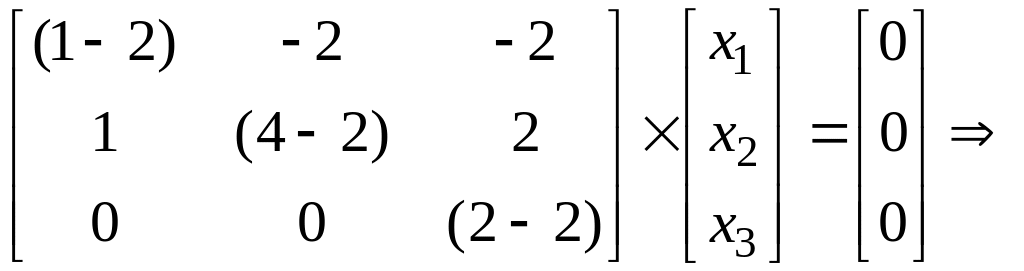
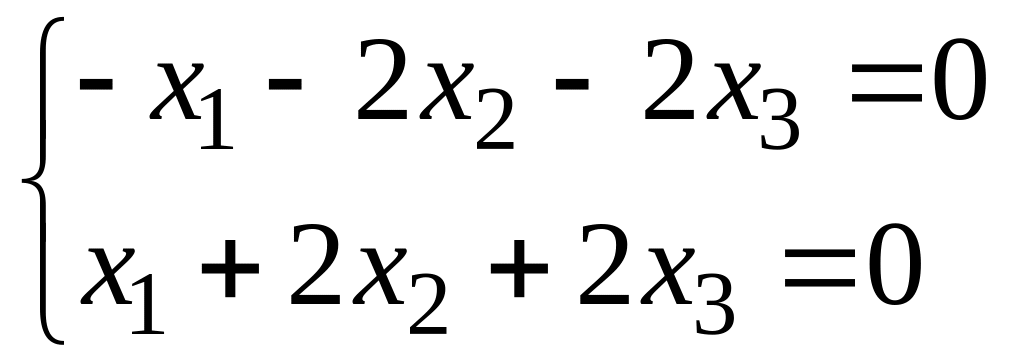
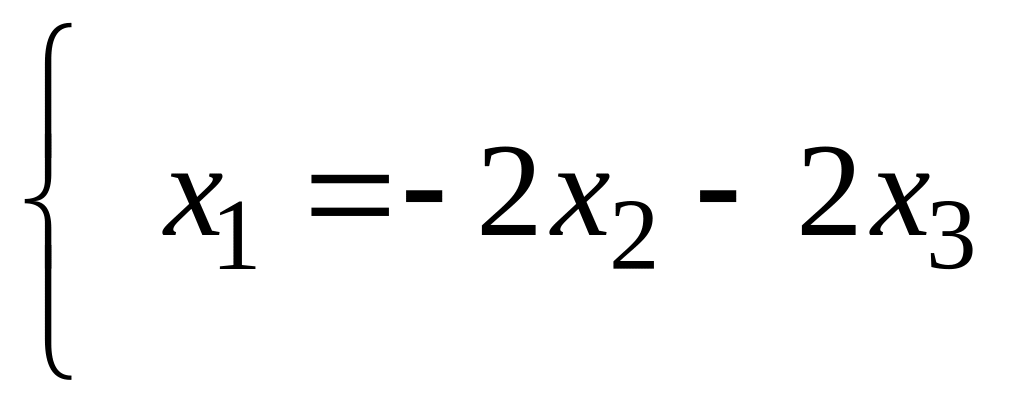
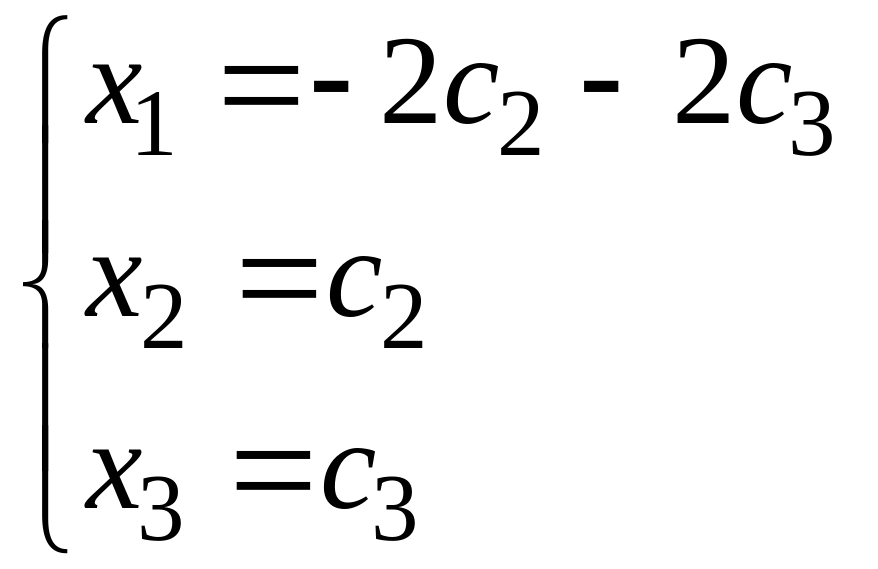
Т.о. X¹= =

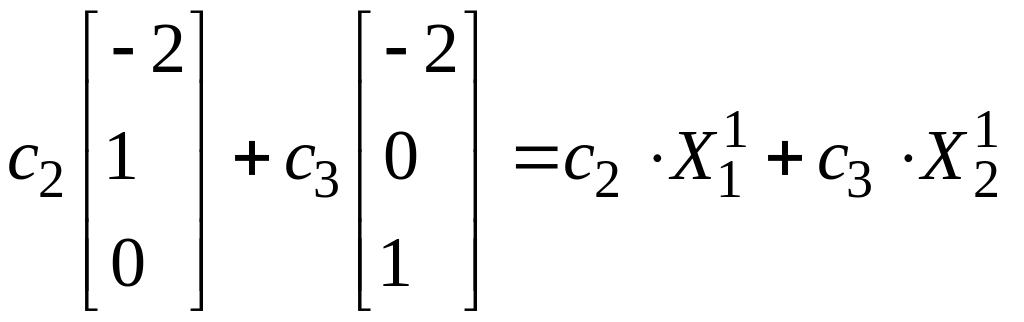
То есть собственному значению λ₁=2 отвечает два линейно независимых вектора 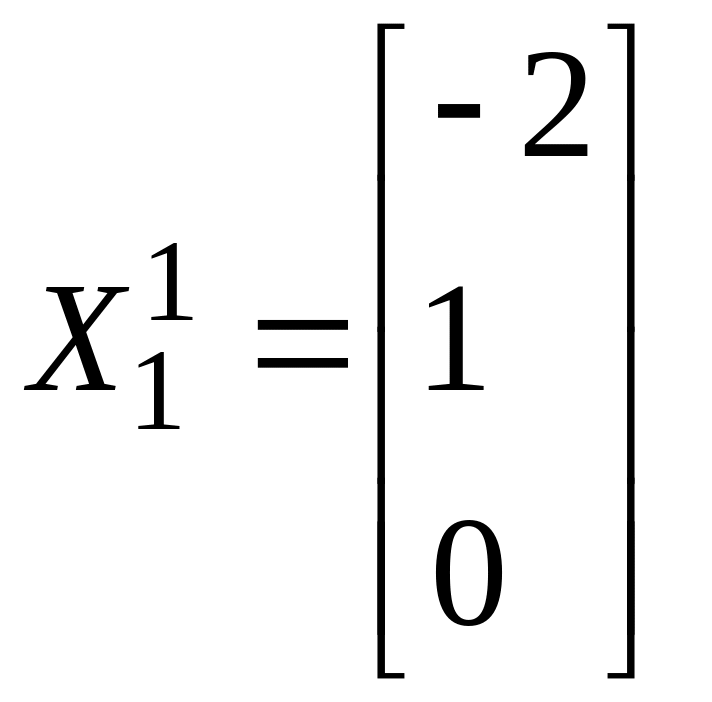и .

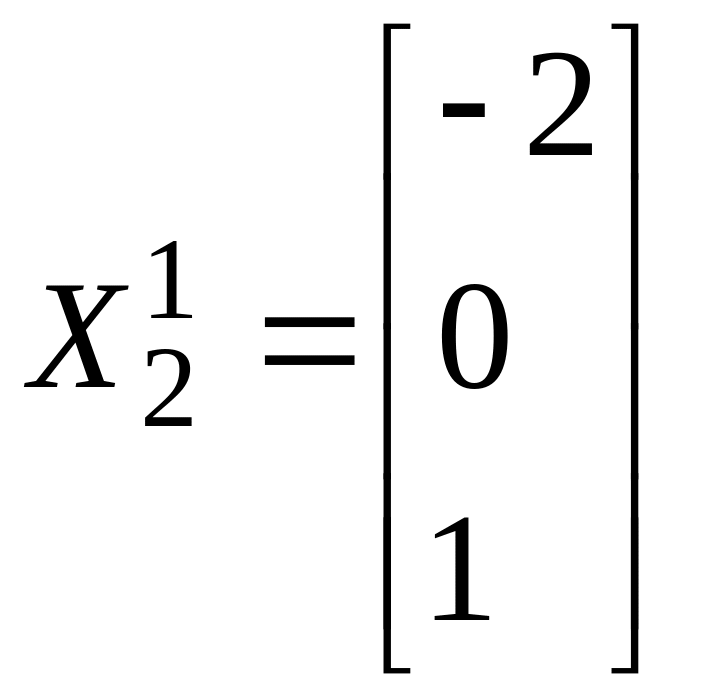При λ₂=3:

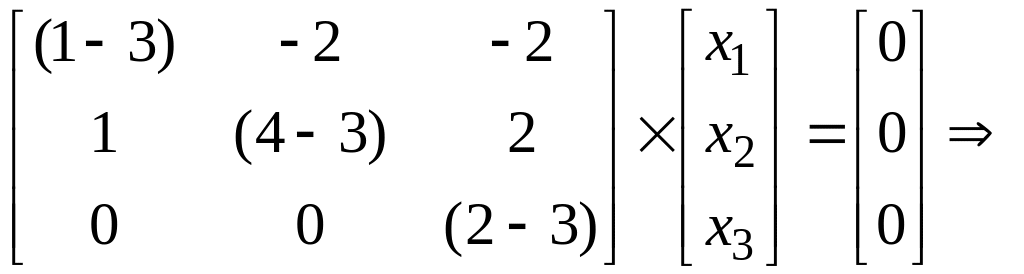
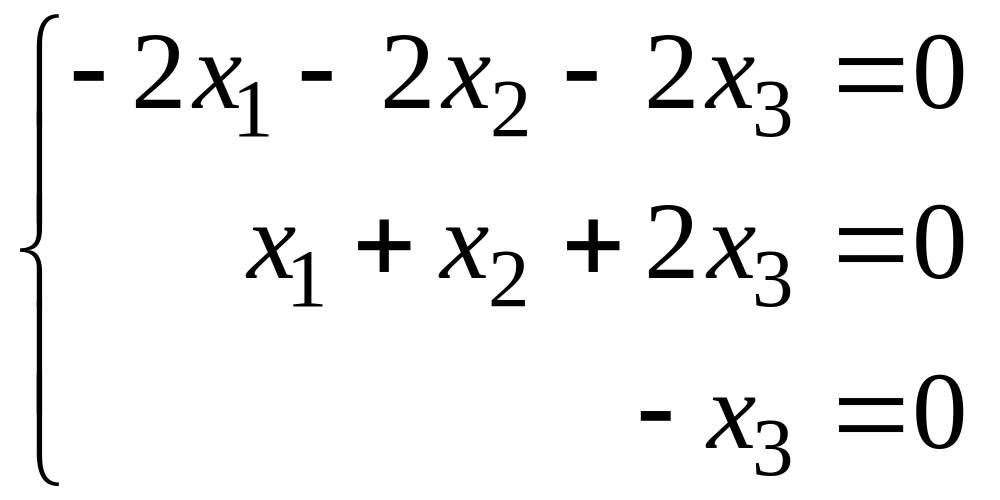
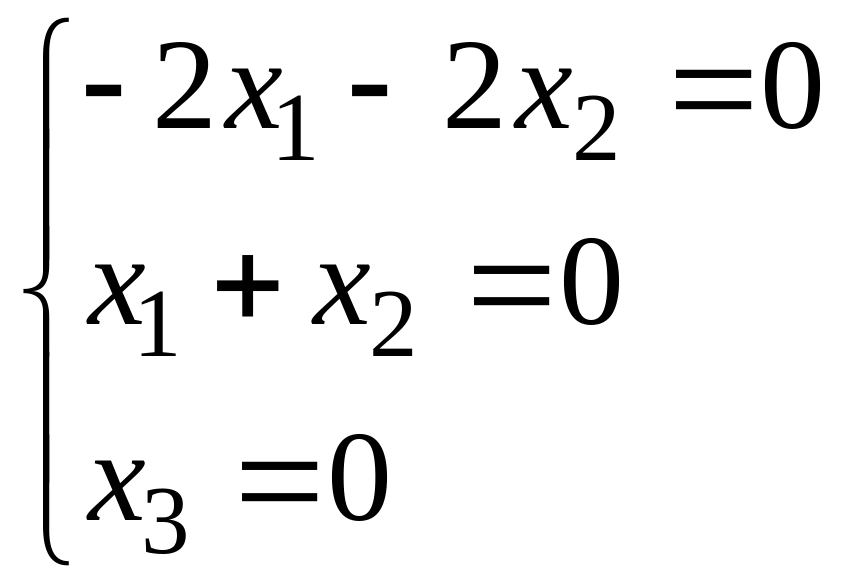
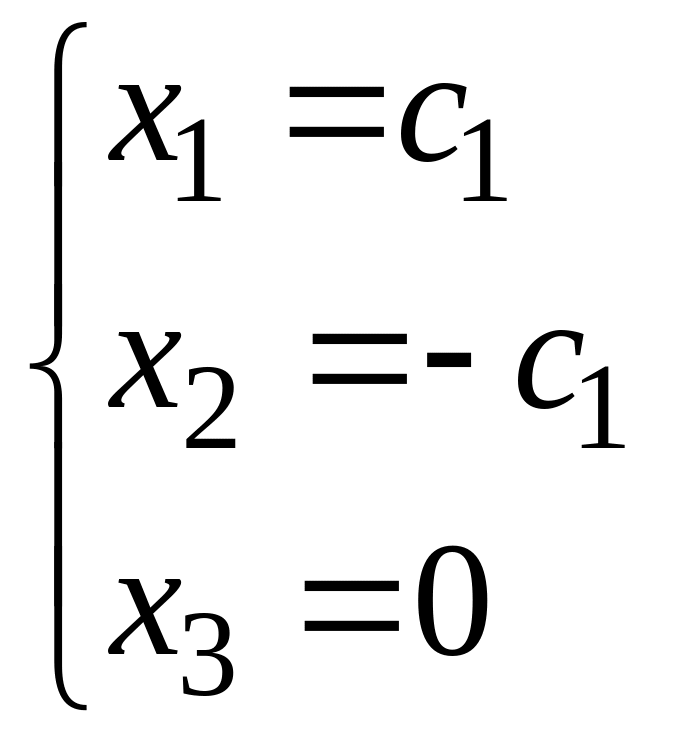
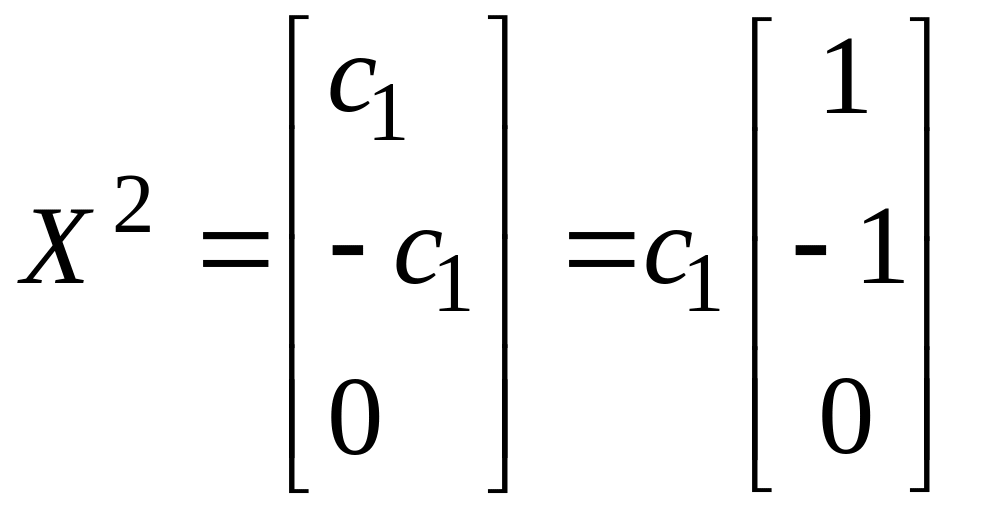
Собственному значению λ₂=3 отвечает собственный вектор

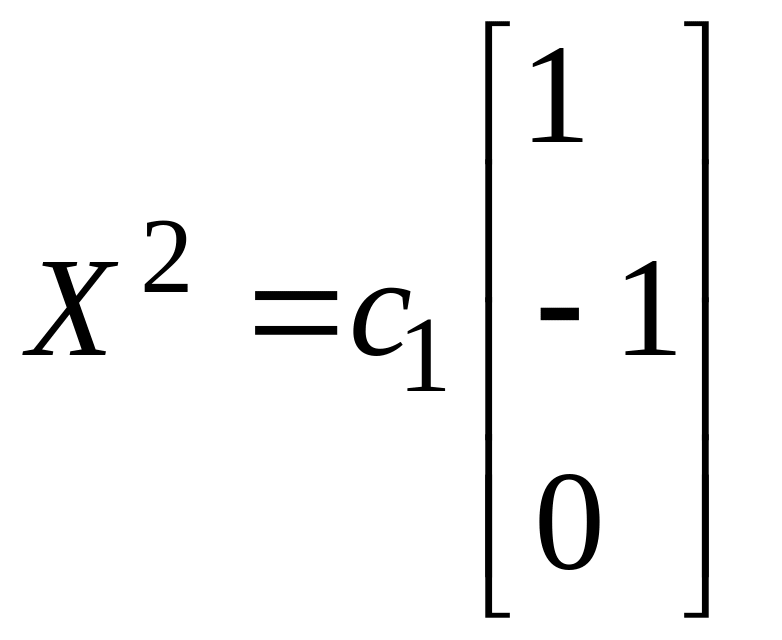
Ответ: векторы образуют базис, в котором матрица А имеет диагональный вид: A_ж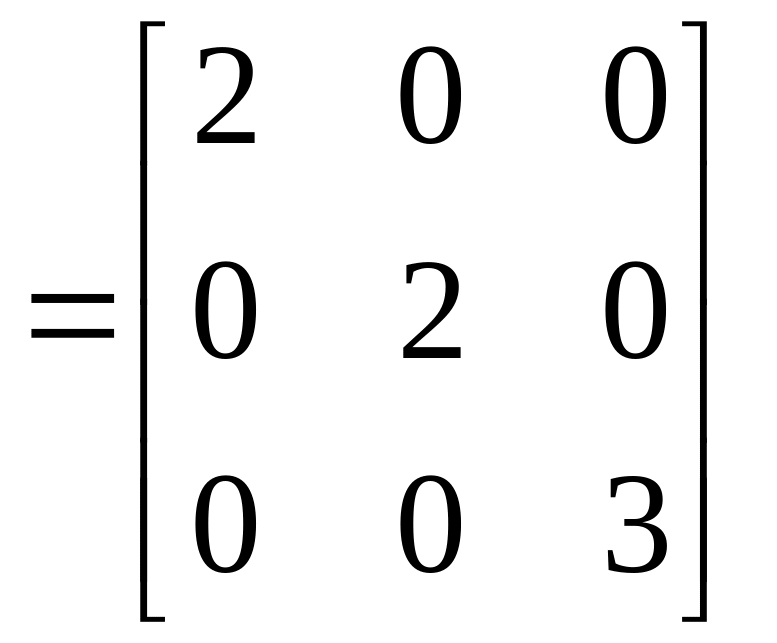 .