
- •Регрессионные модели идентификации: статический объект, понятия о регрессии, парная и множественная регрессия, ошибка идентификации.
- •Диагностирование линейных оу методом комплементарного сигнала. Процедуры диагностирования, оценка работоспособности оу, локализация дефектов по годографу неисправностей.
- •2. Диагностирование линейных оу методом комплементарного сигнала. Постановка задачи, расчет кс по измеренным значениям выходного сигнала.
- •2. Диагностирование линейных оу методом комплементарного сигнала. Постановка задачи, аналитический расчет кс.
- •2. Дифференциальные модели од: метод малого параметра, условия работоспособности.
- •Составить булеву матрицу для конкретной функциональной модели.
- •2. Построение тестов: формулирование задачи, множество проверок, составление булевой матрицы, нахождение элементарных тестов на примере булевой матрицы.
- •2. Авторегрессионные модели идентификации.
- •2. Функциональные модели: задание модели, графическое представление, множество состояний од, таблица неисправностей, неразличимые состояния.
- •Представим степень интеграла в правой части (23) в виде произведения интегралов:
- •2. Линейное прогнозирование состояния од: точечный прогноз
- •2. Составить дробный факторный план (четверть реплики) для модели
- •2. Планы для квадратичных моделей, постановка задачи. Ортогональный центральный композиционный план второго порядка: структура плана, свойства плана.
- •2. Планы для моделей, содержащих линейные члены и взаимодействия различного порядка: дробный факторный план для модели , контраст плана, допустимость плана.
- •2. Оценка состояния объекта по результатам измерения выхода оу, фильтр с конечной памятью.
- •2. Применение дробного фп для модели , правила составления таблицы, смешение оценок коэффициентов модели.
- •Частотный метод определения коэффициентов пф
- •2. Формулы для вычислений и свойства полных и дробных факторных планов для линейных моделей.
- •2. Условия Гаусса – Маркова: проверка случайного характера элементов остаточного ряда
- •2. Оценка адекватности модели оу при проведении параллельных опытов.
- •2. Полные факторные планы первого порядка, определение примеры пфп для , свойства матрицы планирования.
- •Правило построения полных факторных планов
- •2. Дробные факторные планы (дробный факторный эксперимент): дробные реплики, определение, правило построения дробных факторных планов, генератор плана.
- •2. Планы для квадратичных моделей (планы второго порядка), постановка задачи, полные факторные планы
- •2. Метод сопряженных направлений для квадратичной целевой функции.
- •2.Составление булевой матрицы для конкретной функциональной модели.
2. Авторегрессионные модели идентификации.
Поставим задачу
Рассмотрим ОУ с одним входом и одним выходом:

Объект описывается ПФ заданной структуры (1): Объект является устойчивым, а ПФ реализовывается:
 (1)
(1)
Действие
неучтенных факторов при описании объекта
приводит к появлению случайных помехи
![]() . В
ходе экспериментальных исследований
ОУ были получены последовательности
дискретных отсчетов входных и выходных
сигналов объекта. Обозначим эти
последовательности соответственно:
. В
ходе экспериментальных исследований
ОУ были получены последовательности
дискретных отсчетов входных и выходных
сигналов объекта. Обозначим эти
последовательности соответственно:
![]()
Измерение
сигналов в дискретный момент времени
делает необходимым описание объекта с
помощью дискретной ПФ. Используя
соответствие между z
и p,
находим представление p
через комплексную величину z.
![]()
Получаем
дискретную ПФ:
 (2)
(2)
где
![]()
Разделим числитель и знаменатель (2) на n-ую степень z:
 (3)
(3)
В (3) примем z за оператор сдвига (запаздывания):
![]()
С
учетом этого от ПФ
![]() можно перейти к разностному уравнению
(числитель левой части умножить на
знаменатель правой и наоборот; учитывая
сдвиги):
можно перейти к разностному уравнению
(числитель левой части умножить на
знаменатель правой и наоборот; учитывая
сдвиги):
![]()
Это уравнение разрешено относительно выхода в текущий i-ый момент времени и с учетом помехи , можно это выражение представить в виде (4):
![]() (4)
(4)
(4) – алгоритм формирования выхода на основе предшествующих значений входа и выхода
(4) – авторегрессивная модель – описание связи значений одного и того же сигнала в разные моменты времени.
Модель будет иметь ту же структуру, что и (4):
![]() (5)
(5)
неизвестные коэффициенты заменены оценками.
Задача
идентификации сводится к нахождению
оценок коэффициентов (5) так, чтобы
получить результат наилучшим образом
согласующийся с экспериментальными
данными, т.е., чтобы в каждый момент
дискретного времени i
получить достаточно малую ошибку
идентификации
![]() между выходным сигналом ОУ
между выходным сигналом ОУ
![]() и
модели
и
модели
![]() :
:
![]() .
.
Для
каждого дискретного отсчета
![]() составляем уравнение наблюдений
составляем уравнение наблюдений
![]()
– результат измерения выхода (выход в i-ом измерении), правая часть – модель + ошибка идентификации.
В результате получаем систему из N уравнений:

Введем
вектор измерений значений выхода
![]() ;
;
вектор
оценок коэффициентов
![]() ;
;
вектор
ошибок идентификации
![]() ;
;
и прямоугольной матрицы H – матрица наблюдений, элементами которой являются измеренные значения входа и выхода:

В
результате записываются результаты
наблюдений в векторной форме:![]()
Используется критерий качества (целевая функция):
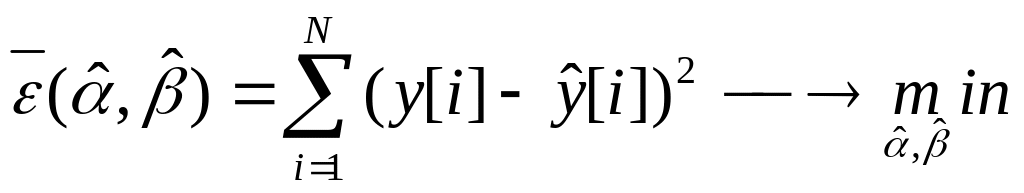
Получаем
![]() – МНК оценки.
– МНК оценки.
Билет №8. 1. Оценка значимости модели: суммы квадратов отклонений и соответствующие им числа степеней свободы, критерий Фишера.
Оценка значимости модели и ее параметров
Вводится
сумма квадратов отклонений выхода
объекта от его среднего значения:![]() (18)где
(18)где
![]() .
.
 – сумма
квадратов отклонений выхода ОУ
относительно среднего значения (общая
сумма квадратов).
– сумма
квадратов отклонений выхода ОУ
относительно среднего значения (общая
сумма квадратов).
![]() -
мат ожидание
-
мат ожидание
 – сумма
квадратов отклонений, вызванная
переменными модели (объясненная часть),
– сумма
квадратов отклонений, вызванная
переменными модели (объясненная часть),
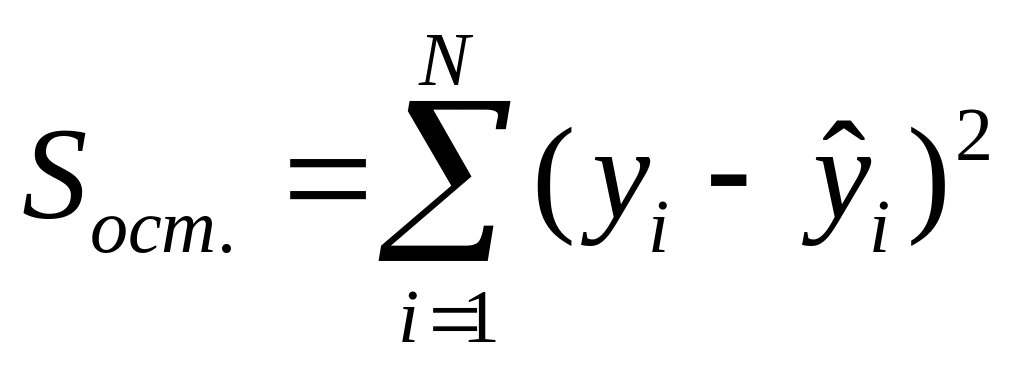 – сумма
квадратов остатков (необъясненная
часть).
– сумма
квадратов остатков (необъясненная
часть).
![]() – результат
неучтенного действия ненаблюдаемых
факторов, показывающих часть дисперсии,
которая порождена ненаблюдаемыми
факторами. Левая часть (18) включает две
составляющие:
– результат
неучтенного действия ненаблюдаемых
факторов, показывающих часть дисперсии,
которая порождена ненаблюдаемыми
факторами. Левая часть (18) включает две
составляющие:
первая – объясняет действие факторов,
вторая – ненаблюдаемые факторы.
Для оценки значимости модели используют коэффициент детерминации:
 (19)
(19)
Показывает, какую долю составляет дисперсия факторов модели в общей дисперсии выхода объекта. Дисперсия выхода объекта пропорциональна общей сумме квадратов отклонений, стоящих в левой части (18). Дисперсия факторов пропорциональна факторной сумме, дисперсия остатков пропорциональна остаточной сумме квадратов.
Если
модель абсолютно точно описывает объект,
т.е. выход модели эквивалентен выходу
объекта (учли все факторы, влияющие на
выход), поэтому остатки равны 0 и
![]() .
.
![]() оценивает
правильность полученной модели.
оценивает
правильность полученной модели.
Каждой сумме квадратов, входящей в (18) соответствует число степеней свободы, показывающих независимые изменения той или иной величины.
![]() – число
степеней свободы. N
находят из среднего значения выхода.
Под числом
степеней свободы
понимают число измерений – число
констант, вычисляемых на их основе.
– число
степеней свободы. N
находят из среднего значения выхода.
Под числом
степеней свободы
понимают число измерений – число
констант, вычисляемых на их основе.
![]() – выход
формируется на основе регрессии,
учитывающей n
входов. n
– число факторов, используемых в модели.
– выход
формируется на основе регрессии,
учитывающей n
входов. n
– число факторов, используемых в модели.
![]()
Критерий Фишера
Значимость модели в целом оценивается с помощью F-критерия Фишера:
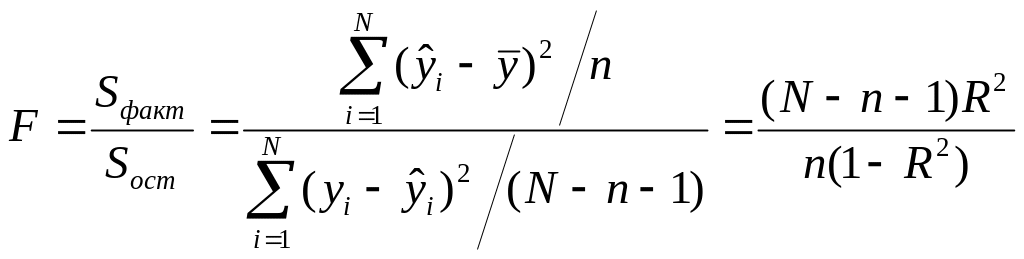 (21)
(21)
где
![]() – факторная сумма квадратов на одну
степень свободы;
– факторная сумма квадратов на одну
степень свободы;
![]() – остаточная
сумма квадратов на одну степень свободы.
– остаточная
сумма квадратов на одну степень свободы.
N – число наблюдений, n – число факторов.
Вычисляется фактическое значение F – критерия по формуле (21). Затем задаются уровнем значимости и по таблице распределения Фишера для степени своды n, которая соответствует , определяются табличные значения распределения Фишера.
Вывод: Модель считается статистически значимой (существенной), если фактическое значение F-критерия (F) превосходит табличное его значение при заданном уровне значимости , т.е. . Если условие не выполняется, то регрессионная модель неадекватна.
Чтобы исключить несущественные факторы, влияющие на выход модели, используется оценка значимости коэффициентов регрессии.
Наблюдение за объектом представим в виде (22):
![]()
– регрессионная модель. (22)
Точность оценивания коэффициентов регрессии определяется ковариационной матрицей:
Если о случайном процессе (22) все известно и известна его дисперсия, то:
![]() (23a)
(23a)
Дисперсия неизвестна. Вместо дисперсии случайной величины используют дисперсию остатков:
 (24)
(24)
Для каждой оценки коэффициентов рассчитывается отношение:
![]() – коэффициент
значимый (существенный),
– коэффициент
значимый (существенный),
– критическое значение распределения Стьюдента для заданного уровня значимости и степеней свободы.
Если выполняется условия, то оценка коэффициентов считается значимой, т.е. наблюдаемый вход модели существенно влияет на её выход. В противном случае делается вывод, что соответствующий вход не существенно влияет на выход и его можно исключить, считая соответствующую оценку коэффициентов равной нулю.
Т.е. после получения модели необходимо совершить множество действий для принятия модели к практической реализации.
e=y-y1; %Невязка (остаточный ряд)
my=sum(y)/N; %Мат.ожидание выхода объекта
dy=(y-my)'*(y-my); %Сумма квадратов отклонений выхода ОУ относ МО
r2=1-sum(e.^2)/dy; %Коэффициент детерминации
F=((N-n-1)*r2)/(n*(1-r2)); %Значение распределения
