2.Составление булевой матрицы для конкретной функциональной модели.

Пример

Рассмотрим диагностируемый объект, состоящий из 5 функциональных элементов В1,В2,В3,В4,В5, соединенных по схеме (рис. 3); y1,y2,y3,y4,y5 – выходы функциональных элементов (направление внешних воздействий V1 и V2 указаны стрелками). Предположим, что неисправная работа объекта диагностики вызывается наличием только одной неисправности, которая локализуется внутри функционального элемента.

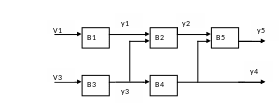
Рис. 3

Тогда множество возможных состояний диагностируемого объекта будет состоять из пяти элементов:

01111 – х1(В1) – неисправный элемент В1;

10111 – х2(В2) – неисправен В2;

............

11110 – х5(В5) – неисправен В5.

Множество возможных проверок определяется 5-ю элементами

П1(y1) – проверка состояния функционального элемента В1 по его выходу y1;

.................

П5(y5) – В5 по выходу y5.

Множество результатов проверок будет состоять из 2-х элементов :

0 – выход функционального элемента не в норме;

1 – выход функционального элемента в норме.

Тогда табл. состояний диагностируемого объекта запишется в виде:

Табл. (*)

	П1	П2	П3	П4	П5
х1(В1)	0	0	1	1	0
х2(В2)	1	0	1	1	0
х3(В3)	1	0	0	0	0
х4(В4)	1	1	1	0	0
х5(В5)	1	1	1	1	0

5 столбец можно исключить

На основании таблицы неисправностей составляют булеву матрицу. Берем попарно неразличимые состояния (xor)

	П1	П2	П3	П4
(x1,x2)	1	0	0	0
(x1,x3)	1	0	1	1
(x1,x4)	1	1	0	1
(x1,x5)	1	1	0	0
(x2,x3)	0	0	1	1
(x2,x4)	0	1	0	1
(x2,x5)	0	1	0	0
(x3,x4)	0	1	1	0
(x3,x5)	0	1	1	1
(x4,x5)	0	0	0	1

По данной таблице составляют логическое выражение:

-- 3 проверки

Проверки (по табл. (*)):

1. П1 =0, П2=0, П4=1 – неисправен В1

2. П1=1, П2=0, П4=1 – неисправен В2

3. П1=1, П2=1, П4=0 – неисправен В4

1.Регрессионные модели идентификации: статический объект, понятие о регрессии, парная и множественная регрессия, ошибка идентификации.1-3

2.Диагностирование линейных ОУ методом комплементарного сигнала: оценка работоспособности ОД, локализация дефектов по годографу неисправностей.4-5

3.Численные методы оптимизации: метод Ньютона и квазиньютоновские методы, их особенности. 6-7

4.Диагностирование линейных ОУ методом комплементарного сигнала: постановка задачи, расчет КС по измеренным значениям выходного сигнала объекта. 8-9

5.Оценка параметров линейной регрессионной модели: критерий идентификации, МНК – оценки коэффициентов модели, точность оценок.10-11

6.Диагностирование линейных ОУ методом комплементарного сигнала: постановка задачи, аналитический расчет КС. 12-13

7.Аппаратная реализация процесса идентификации.14

8.Дифференциальные модели ОД.15-16

9.Нелинейные регрессионные модели, приведение нелинейных моделей к линейным 17

10.Составление булевой матрицы для конкретной функциональной модели (пример).18-19

11.Оценка адекватности модели. Условия Гаусса – Маркова: проверка центрированности и некоррелированности остаточного ряда.20-21

12.Построение тестов: формулирование задачи, множество проверок, составление булевой матрицы.22-23

13.Оценка значимости коэффициентов регрессионной модели при неизвестной дисперсии случайной составляющей.24-25

14.Авторегрессионные модели идентификации.26-27

15.Оценка значимости модели: суммы квадратов отклонений и соответствующие им числа степеней свободы, критерий Фишера.28-30

16.Функциональные модели: задание модели, графическое представление, множество состояний ОД, таблица неисправностей, неразличимые состояния.31

17.Идентификация нелинейных безынерционных объектов.32-33

18.Линейное прогнозирование состояния ОД: точечный прогноз 34-35

19.Линейное прогнозирование состояния ОД: доверительные интервалы.36-37

20.Составить дробный факторный план (четверть реплики) для модели

. 38

21.Некорректность задачи идентификации, регуляризующие алгоритмы оценки весовой функции, оценка импульсной функции при входном «белом» шуме. 39-40

22.Планы для квадратичных моделей, постановка задачи. Ортогональный центральный композиционный план второго порядка: структура плана, свойства плана.41-42

23.Условие идентифицируемости автономной динамической системы.43

24.Планы для моделей, содержащих линейные члены и взаимодействия различного порядка: дробный факторный план для модели , контраст плана, допустимость плана.44-45

25.Численные методы оптимизации: градиентные методы, особенности методов.46-47

26.Оценка состояния объекта по результатам измерения выхода ОУ, фильтр с конечной памятью.48-50

27.Идентификация нелинейных динамических объектов: модель Гаммерштейна. 51-52

28.Применение дробного ФП для модели , правила составления таблицы, смешение оценок коэффициентов модели. 53-55

29.Параметрическая идентификация односвязных линейных объектов: частотный метод определения коэффициентов ПФ, общий случай. 56-57

30.Формулы для вычислений и свойства полных и дробных факторных планов для линейных моделей.58-60

31.Частотный метод определения коэффициентов ПФ объекта . 61-62

32.Условия Гаусса – Маркова: проверка случайного характера элементов остаточного ряда 63

33.Частотный метод определения коэффициентов ПФ объекта . 64-65

34.Оценка адекватности модели ОУ при проведении параллельных опытов. 66-67

35.Описание нелинейных стационарных ОУ функциональными рядами Вольтера, ядра Вольтера, структурная схема модели нелинейного объекта, параметризация модели. 68-70

36.Полные факторные планы первого порядка, определение примеры ПФП для , свойства матрицы планирования. 71-73

37.Применение дискретных моделей при идентификации непрерывного ОУ, дискретная модель непрерывного объекта, выбор периода дискретизации. 74-75

38.Дробные факторные планы первого порядка: дробные реплики, определение, правило построения дробных факторных планов, генератор плана. 76

39.Оценка параметров нелинейного статического ОУ. 77

40.Планы для квадратичных моделей (планы второго порядка), постановка задачи, полные факторные планы 78-79

41.Корреляционные методы идентификации: уравнение Винера-Хопфа, нахождение корреляционных функций, параметрический метод решения уравнения Винера-Хопфа 80-81

42.Метод сопряженных направлений для квадратичной целевой функции.82

43.Корреляционные методы идентификации: дискретный аналог уравнения Винера-Хопфа.83-84

44.Составление булевой матрицы для конкретной функциональной модели.85-86