1.Дайте определение передаточной функции лсс.

а) Это отношение изображения выходного сигнала к изображению входного сигнала.

б) Это отношение изображения входного сигнала к изображению выходного сигнала.

в) Реакция системы на единичный импульс.

г)Реакция системы на единичную ступенчатую функцию.

2.Для каких звеньев переходная функция неограниченно возрастает с течением времени?

а) интегрирующие звено; дифференциальное звено.

б) усилительное звено; запаздывающее звено.

в) интегрирующее звено; апериодическое звено 1-ого порядка;

г) форсирующее звено 1-ого порядка; усилительное звено

3. Входной сигнал лсс с одним входом и одним выходом увеличивается в три раза. Как изменился выходной сигнал?

а) не изменился

б) увеличился в три раза

в) уменьшился в три раза

г) увеличился в шесть раз

4. Как изменяется постоянная времени Т₁ и коэффициент усиление К₁ апериодического звена, если его охватить гибкой отрицательной обратной связью с передаточной функцией W₂(p) = K₀p?

а) увеличится Т₁, К₁ остается неизменным

б) уменьшится Т₁, К₁ остается неизменным

в) увеличится Т₁, К₁ увеличится

г) увеличится Т₁, К₁ уменьшится

5.Как изменяется постоянная времени, коэффициент усиления и форма переходного процесса звена с W₁(P) = при охвате его звеном жесткой отрицательной обратной связи W₂ (p) = K₀ ?

W₁(P)

x(p) y(p) .

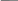
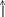
W₂(P)

+

а) постоянная времени и коэффициент усиления уменьшаются, форма переходной функции изменится.

б) постоянная времени и коэффициент усиления уменьшаются, форма переходной функции не изменится.

в) постоянная времени и коэффициент усиления увеличится, форма переходной функции изменится.

г) постоянная времени и коэффициент усиления останутся неизменны, изменится форма переходной функции.

W₁(P)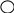

6.Изменяется ли постоянная времени, коэффициент усиления и форма переходного процесса звена с передаточной функцией W₁(P) = при охвате его звеном гибкой отрицательной обратной связи W₂ (p) = K₀ , x y

W₂(P)

-

а) изменяется Т₁, изменяется форма переходной функции, изменяется коэффициент усиления.

б) не изменяется Т₁, изменяется форма переходной функции, коэффициент усиления не изменяется

в) изменяется Т₁, не изменяется форма переходной функции, коэффициент усиления не изменяется

г) изменяется Т₁, изменяется форма переходной функции, коэффициент усиления не изменяется

7.Определите w(p) системы по структурной схеме

W₂(P)

W₁(P)

x y

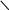
W₃(P)

W₄(P)

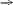
а) W(p) = W₁(W₂·W₄)+W₃

б) W(p) = W₁(W2+W4)+W₃

в) W(p) = W₁+(W₂·W₄)+W₃

г) W(p) = W₁(W₂+W₄)·W₃

8. Определите w(p) по структурной схеме

W₂(P))

W₁(P)

x y

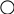
W₃(P)

-

а)W(p) = (W₁+W₂)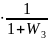

б) W(p) = (W₁+W₂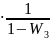

в) W(p) = (W₁·W₂)

г) W(p) = (W₁+W₂)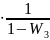

9. Какой частоте ω соответствует точка, отстоящая на логарифмической шкале от точки ω=1, на 40 мм (логарифмическая шкала выполнена в масштабе 1 декада - 50 мм).

а) ω=6,3

б) ω=3,3

в) ω=0,8

г) ω=1

10. Переведите в децибелы коэффициент усиления К = 15 безынерционного звена .

а) 20lg15 = 20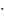 1,1761 = 23,52 дБ

б) 20log15 = 20 1,043 = 19,52 дБ

в) 20lg(-15) = 20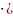 1,1761) = -23,52 дБ

г) 20log15 = 20 1,122 = 20,51 дБ