41

Лекция 7.

Редукция приводимых представлений.

В приложениях теории групп часто возникают приводимые представления, которые необходимо представить в виде суммы неприводимых. Во многих случаях редукция осуществляется непосредвенно подбором неприводимых представлений, дающих в сумме приводимое. Однако имеется и систематическая процедура приведения. Эта процедура основана на том, что неприводимые представления образуют систему взаимонезависимых, ортогональных векторов. Используя нормировочный множитель n^-1/2 (n – порядок группы) условие ортогональности можно записать в виде выражения:

Суммирование проводится по всем элементам симметрии; _i – характер элемента симметрии в - или -ом неприводимом представлении. При суммировании по классам получается следующее соотношение:

где n_i – порядок i-го класса; k – число классов в группе. Если в этих соотношениях вместо неприводимого представления Г_ использовать приводимое представление Г, то результат будет равен нулю, если Г_ не входит в приводимое представление Г. Если Г_ входит в приводимое представление Г, то в результате получим число, равное кратности вхождения -го неприводимого представления в приводимое. Это число можно определить по формуле:

В качестве примера рассмотрим группу C_6v и перемножим характеры представлений E₁ и E₂. Полученное при перемножении приводимое представление представим затем в виде суммы неприводимых представлений.

C6v	E	2C6	2C3	C2	3v	3d
E1	2	1	-1	-2	0	0
E2	2	-1	-1	2	0	0
E1E2	4	-1	1	-4	0	0
Характеры остальных представлений в группе
A1	1	1	1	1	1	1
A2	1	1	1	1	-1	-1
B1	1	-1	1	-1	1	-1
B2	1	-1	1	-1	-1	1

Редукция приводимого представления E₁E₂.

a_A1=1/12[1·1·4 + 2·1·(-1) + 2·1·1 + 1·1·(-4) + 0 + 0] = 1/12[4-2+2-4] = 0

a_A2=1/12[1·1·4 + 2·1·(-1) + 2·1·1 + 1·1·(-4) + 0 + 0] = 1/12[4-2+2-4] = 0

a_B1=1/12[1·1·4 + 2·(-1)·(-1) + 2·1·1 + 1·(-1)·(-4) + 0 + 0] = 1/12[4+2+2+4] = 1

a_B2=1/12[1·1·4 + 2·(-1)·(-1) + 2·1·1 + 1·(-1)·(-4) + 0 + 0] = 1/12[4+2+2+4] = 1

a_E1=1/12[1·2·4 + 2·(-1)·1 + 2·(-1)·1 + 1·(-2)·(-4) + 0 + 0] = 1/12[8-2-2+8] = 1

a_E2=1/12[1·2·4 + 2·(-1)·(-1) + 2·(-1)·1 + 1·2·(-4) + 0 + 0] = 1/12[8+2-2-8] = 0

Таким образом: E₁E₂ = B₁ + B₂ + E₁.

Метод проекционных операторов.

Часто требуется построение функций преобразующихся по определенному неприводимому представлению. Такая процедура применяется, например, при постороении нормальных колебательных мод, молекулярных орбиталей с определенной симметрией и т.д. Наиболее систематическая процедура построения таких функций опирается на метод проекционных операторов.

При воздействии проекционного оператора на функцию возникает функция, соответствующая определенному неприводимому представлению группы. Т.е.

f^ - функция, соответствующая -му неприводимому представлению;

n_ - размерность -го неприводимого представления;

n - порядок группы;

f - исходная функция;

P^ - проекционный оператор, соответствующий -му неприводимому

представлению;

P^ определяется в виде суммы: где характер операции симметрии R в -ом неприводимом представлении; сумма по всем операциям. Т.о. где произведение Rf – определяет новую функцию f_R - результат действия операции симметрии R на исходную функцию f. В итоге получаем

Однако, если функция f не принадлежит к данному неприводимому представлению, то результат действия проекционного оператора равен нулю.

Для того, чтобы получить функцию с заданной симметрией необходимо знать характеры группы и то как преобразуется функция по отношению к различным операциям симметрии группы.

Рассмотрим проектирование функций от x и y для разных представлений группы D₄.

Операции симметрии группы D₄ изображены ниже на рис.

Р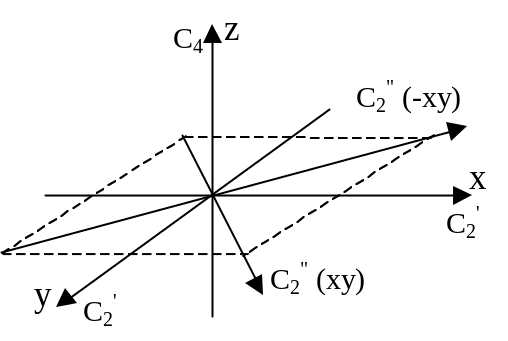 езультат действия операций симметрии группы D₄ на функции x, y, x², y² и xy.

D4		2C4			2C2'		2 C2"
	E	C4	C43	C2z	C2'x	C2'y	C2"(xy)	C2"(-xy)
x	x	y	-y	-x	x	-x	y	-y
y	y	-x	x	-y	-y	y	x	-x
x2	x2	y2	y2	x2	x2	x2	y2	y2
y2	y2	x2	x2	y2	y2	y2	x2	x2
xy	xy	-xy	-xy	xy	-xy	-xy	xy	xy

Характеры группы d4.

D4	E	2C4	C2z	2C2'	2 C2"
A1	1	1	1	1	1
A2	1	1	1	-1	-1
B1	1	-1	1	1	-1
B2	1	-1	1	-1	1
E	2	0	-2	0	0

Построим функции симметрии А₁ их Х

Р^A1(х)=1/8[1·x+1·y+1· (-y)+1· (-x)+1·x+1· (-x)+1·y+1· (-y)]=0

Т.о. функция х не принадлежит представлению А₁.

Р^E(х)=2/8[2·x+0·y+0· (-y)+(-2)· (-x)+0·x+0· (-x)+0·y+0· (-y)]=

2/8·4x=x

Р^A1(х²)= . . . =1/2(x²+y²)

Р^B1(х²)= . . . =1/2(x²-y²)

Спроецируем полином x²+2xy+y² на представление B₂. Проецируется каждое слагаемое и затем результаты суммируем.

Р^B2(х²)= . . . =0

Р^B2(2хy)= . . . =2xy

Р^B2(y²)= . . . =0

Т. о. Р^B2(x²+2хy+y²) = . . . = 2xy