23

Применение теории групп симметрии в химии.

Лекция 1.

Математическое введение.

Многие физические объекты обладают свойственной им симметрией. Рассмотрение этой симметрии помогает в исследованиях свойств объектов. Например, для проведения полного квантовохимического исследования молекулы бензола с использованием ее симметрии необходимо описать только одну из связей С-Н и С-С. Часто поведение объекта при некоторых условиях определяется присущей ему симметрией. Симметрия молекулы накладывает ряд ограничений на ее взаимодействие с электромагнитным излучением и, следовательно, на ее спектральные свойства. Знание этих ограничений дает ценную информацию о структуре молекулы.

Изучение симметрии молекулы начинается прежде всего с определения операций симметрии. Совокупность всех операций симметрии составляет математическую группу. Свойства групп хорошо известны из теории групп. Т.о. симметрия объекта может быть удобно сформулирована в рамках теории групп.

При исследовании свойств симметрии физических объектов необходимо точно определить результаты ряда операций симметрии. Эта задача часто требует преобразования координат точки в некоторой выбранной системе координат. Такие преобразования обычно записываются в векторном или матричном виде. Поэтому необходимо предварительно кратко повторить основные операции с векторами и матрицами.

Вектор - геометрически это направленный отрезок прямой. Длина отрезка - модуль вектора.

Сложение векторов:

Вычитание: , можно заменить суммой , где - вектор по направлению обратный .

Сложение и вычитание векторов удовлетворяет ассоциативному и коммутативному законам, т.е. эти операции можно выполнять в любом порядке, а участвующие в них вектора группировать.

Умножение векторов.

1. Скалярное произведение.

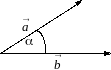
Результат произведения - скаляр равный

Выполняется коммутативный закон.

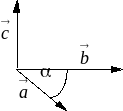
2. Векторное произведение

модуль равен: c=a b Sin()

- не подчиняется

коммутативному закону

3. Прямое (тензорное) произведение векторов

Обозначается как . Результат произведения - матрица.

Вектора в декартовом пространстве.

Вектор в декартовом пространстве можно представить в виде:

или как

вектор-строка , или вектор столбец

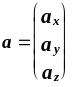
Скалярное произведение.

,

т.к. и или можно записать как .

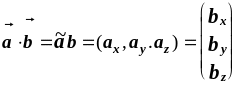Векторное произведение.

Прямое произведение. , где С - матрица размерностью nn (n - размерность векторов a и b. Или

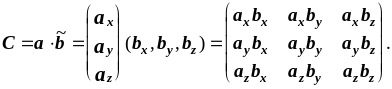
Матрицы.

Обратная - это матрица, которая при умножении на данную дает единичную. Т.е. . Матрица, у которой детерминант равен нулю, называется сингулярной и не имеет обратной. Неквадратные матрицы не имеют обратных, т.к. их детерминант не определен.

Комплексно-сопряженная - знак мнимой части каждого элемента заменен на обратный. Если - действительная, то .

Транспонированная - строки заменяются на столбцы.

Симметричная.

Кососимметричная.

Эрмитово-сопряженная ; одновременно применяются операции комплексного сопряжения и транспонирования.

Если - матрица просто эрмитова.

Свойства матриц.

, , .

Прямое произведение матриц.

.

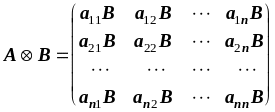Унитарная матрица.

Если , то матрица - унитарная ее детерминант равен 1.

Унитарное преобразование матрицы : .

Вращение вектора можно представить как произведение матриц , где - матрица преобразования координат; - вектор-столбец исходных значений координат. В двухмерном случае поворот на угол  задается матрицей:

.

Эта матрица определяет поворот вектора на угол  по часовой стрелке или поворот системы координат против часовой стрелки. (Угол  - положительный.)

Поворот, обратный данному, есть поворот на угол (-). Т.о. матрица

.

Учитывая, что и получим

.

Т.о. , следовательно матрица - унитарная.

В трех измерениях матрица поворота имеет вид:

.

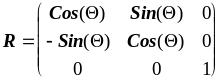Третье измерение - ось поворота.

Операции симметрии.

Рассмотрим множество операций симметрии, используемых при описании молекул. Операция симметрии - действие при применении которого конфигурация объекта совпадает с первоначальной. Операция симметрии должна быть определена по отношению к элементу симметрии. Элемент симметрии - это геометрический объект, такой, как плоскость, линия, точка, относительно которого выполняет операция симметрии.

Существует пять различных типов элементов симметрии, которыми может обладать изолированный объект.

• Тождественная ( или единичная ) операция. Эта операция либо ничего не делает с системой, либо возвращает ее в исходное состояние (поворот на 360^о).

• Ось вращения. Если поворот на угол 2/n приводит к конфигурации совпадающей с исходной, то он называется поворотом типа C_n. Поворот осуществляется по часовой стрелке. Соответствующий элемент симметрии C_n - собственная ось поворота n-го порядка. Поворот на угол, кратный некоторому элементарному углу (т.е. на угол m2/n), обозначается как C_n^m . Если кратный поворот можно выразить через поворот более низкого порядка, то используется обозначение поворота низкого порядка. Многие системы обладают несколькими собственными осями симметрии. В этом случае ось наивысшего порядка называется главной осью. Если имеется несколько осей одного и того же порядка, то одну из них произвольно выбирают главной.

• Плоскость симметрии. Обозначение - . Плоскости симметрии в зависимости от их связи с главной и вспомогательной осями разделяются на три типа. Существуют: вертикальная плоскость симметрии _v , содержащая главную ось; диэдральная плоскость симметрии _d , которая содержит главную ось и делит угол пополам между вспомогательными осями 2-го порядка, перпендикулярными к главной оси, или иногда содержит другие элементы; горизонтальная плоскость симметрии _h , перпендикулярная главной оси.

• Несобственная ось поворота или зеркально-поворотная ось n-го порядка. Обозначается как S_n. Представляет собой поворот относительно C_n с последующим отражением в горизонтальной плоскости _h , перпендикулярной этой оси. Элементы симметрии C_n и _h могут в отдельности не существовать.

• Точка инверсии (i). При отражении в этой точке любая точка пространства с координатами (x,y,z) переходит в точку с координатами (-x,-y,-z).

Лекция 2.

Рассмотрим операции симметрии на примере молекулы аммиака NH₃. Геометрическое строение этой молекулы - тригональная пирамида, в основании которой лежат атомы водорода, образующие правильный треугольник. [Нарисовать структуру и пронумеровать атомы водорода как показано на рис. 1]. При операциях симметрии происходит взаимозамещение атомов водорода ; атома азота остается неподвижным. Поэтому для иллюстрации операций симметрии рассмотрим только атомы водорода и для этого их пронумеруем (рис.1). [Далее подробно рассмотреть действие операций симметрии E, C₃, C₃ ² , _v , _v^ , _v^ в соответствии с рис. 2]. Оси поворота проходят по оси z, плоскости включают ось поворота и один из атомов водорода (см. рис. 2). Поворот - по часовой стрелке.

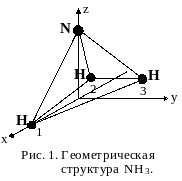
Используя рис. 2 можно легко определить результат последовательного выполнения ( или произведения )двух операций симметрии. При этом расположение элементов симметрии (т.е. осей поворота и плоскостей) в декартовом пространстве остается неизменным. В итоге для рассматриваемого примера можно составить таблицу произведений операций симметрии (см. ниже).

Таблица 1. Произведения операций симметрии.

	E	C3	C3 2	v	v	v
E	E	C3	C3 2	v	v	v
C3	C3	C3 2	E	v	v	v
C3 2	C3 2	E	C3	v	v	v
v	v	v	v	E	C3 2	C3
v	v	v	v	C3	E	C3 2
v	v	v	v	C3 2	C3	E

Каждый элемент таблицы - результат последовательного выполнения 2-х операций симметрии. Первой выполняется операция соответствующая столбцу, второй - строке.

[Подробно рассмотреть построение таблицы на примере 2 и 4-го столбцов. Остальные столбцы могут быть заполнены самостоятельно. На примере таблицы показать, что операции симметрии молекулы NH₃ удовлетворяют групповым теоремам.]

Групповые теоремы:

1. Произведение 2-х элементов дает третий элемент, также являющийся элементом группы.

2. Выполняется ассоциативный закон. Т.е. (ab)c=a(bc). Рассмотрим тройное произведение C₃_vC₃ ² :

(C₃_v)C₃ ² = _v^ C₃ ² = _v^

C₃(_vC₃ ² ) = C₃ _v^ = _v^ .

3. В группе есть элемент, коммутирующий с любым другим элементом и оставляющим его неизменным. Это единичный элемент. EA=AE=E.

4. Элемент, обратный к каждому элементу группы, также является элементом группы. Например: C₃ C₃ ² = C₃ ² C₃. Отражения в плоскости обратны сами себе.

Таким образом операции симметрии NH₃ удовлетворяют групповым постулатам и составляют математическую группу. Аналогичная ситуация имеет место и для любых других систем. Группы, описывающие симметрию ядер молекулы, называются точечными, т.к. все элементы симметрии пересекаются, по крайней мере, в одной точке.