5.Інтерполяційний многочлен Лагранжа.Лінійне та квадратичне інтерполювання.

Нехай при вивченні деякого явища виявилось, що існує функціональна залежність між змінними величинами . Функція залишається нам невідомою, але внаслідок експерименту встановлено значення цієї функції при відповідних значеннях аргументу .

Задача полягає в тому, щоб знайти просту функцію, наприклад многочлен, який наближено зображував би функцію .

Сформулюємо цю задачу точніше.

Нехай на відрізку задані значення функції в точках

Треба знайти многочлен n-го степеня

, (1)

значення якого в точках збігаються із значеннями функції , тобто

Ця задача називається задачею інтерполяції, многочлен (1) – інтерполяційним многочленом, а точки - вузлами інтерполяції. Вважаючи інтерполяційний многочлен наближеним аналітичним виразом для функції , тобто , можемо знаходити наближені значення функції в точках , що лежать між вузлами.

Можна показати, що задача інтерполяції має єдиний розв’язок, причому інтерполяційний многочлен має вигляд:

(2)

Формула (2) називається інтерполяційним многочленом Лагранжа.

Зауваження. У випадку лінійної інтерполяції припускаємо, що графіком функції буде пряма, звідси випливає приріст функції пропорційний приросту аргументу. Якщо задане значення аргументу х знаходиться між наведеними в таблиці

х₀ і х₁, х₁ = х₀ + h i y₀ = f(x₀), y₁ = f(x₀) + Δf, тоді вважають, що

f(x) ≈ f(x₀) + ∆f.

Приклад:

х	2	2,04
у	2,42	2,88

х₀ = 2, х₁ = 2,04, х ≈ 2,008, h = x₁ – x₀

y₀ = 2.42, y₁ = 2.88

f(x) =2,42 + 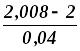× (2,88 – 2,42) ≈ 2,512

Якщо n = 2, то:

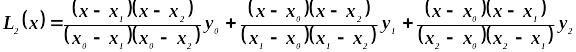– формула квадратичного інтерполювання.

Приклад.

х	0	2
f(x)	1	4

Якщо n = 1, то:

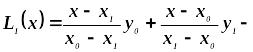формула лінійного інтерполювання.

L₁(x) = × 1 + × 4 = + 2x = = = 1,5x + 1.

Приклад.

х	0	1	2
у	2	1	-3

n = 2

L₂(x) = 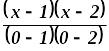× 2 + × 1 + × (-3) =

= × 2 + + × (-3) = x² – 3x + 2 – x² + 2x – 1,5x² + 1,5x = -1,5x² + 0,5x + 2.

6.Поняття n-вимірного простору. Дії над векторами.

Означення . Упорядкована множина п дійсних чисел називається п-вимірним вектором х і позначається х = ( ) або

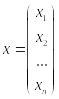
Числа - називаються координатами вектора х. Число п називається розмірністю вектора х. Перехід від запису вектора у вигляді стовпця до запису у вигляді рядка називається транспонуванням вектора.

( - координати вектора).

Означення : Множина всіх п –вимірних векторів називається п –вимірним простором і позначається .

Векторні простори можна розглядати відповідно як множину векторів на прямій, на площині та у тривимірному просторі. На відміну від векторів числа називаються скалярами.

Означення . Два вектори називаються рівними, якщо рівні між собою їх відповідні координати.

Означення . Вектор називається нульовим, якщо всі його координати рівні нулю.

Означення . Вектор називається протилежним до даного, якщо всі його координати протилежні числа до координат даного вектора.

Як зображаються вектори на прямій, на площині та у тривимірному просторі ви знаєте зі школи. Ми нагадаємо які дії можна виконувати над векторами.

Означення: Сумою двох векторів і називається вектор , координати якого дорівнюють сумі відповідних координат векторів-доданків:

.

Означення: Добутком числа на вектор називається вектор , координати якого дорівнюють добутку на відповідні координати вектора :

.

Означення: Вектори a і b називаються колінеарними, якщо їх відповідні координати пропорційні:

.

Властивості додавання векторів та множення числа на вектор

1. 

2. 

3. 

4. 

5. 

6. 

7. 

8. 

9. 

Означення: Скалярним добутком двох векторів і називається число, що визначається сумою попарних добутків відповідних координат:

.

Існує теорема, яка говорить про те, що скалярний добуток векторів можна обчислити ще так:

, де - кут між векторами . Тоді

.

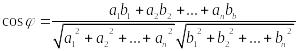Із означення скалярного добутку випливають такі його властивості:

1. 

2. 

3. 

4. 

Означення: Два вектори, скалярний добуток яких дорівнює нулю, називаються взаємно ортогональними.

Нульовий вектор ортогональний до будь-якого вектора.