
- •Три типи лопатей робочого колеса насоса
- •Підбір відцентрового насоса за заданими робочими параметрами
- •Нерівномірність подачі. Побудова графіків подачі
- •Вирівнювання подачі повітряними ковпаками
- •Кулачкові ротаційні насоси
- •Подача насоса і шляхи її досягнення
- •Багатопластинчасті насоси
- •Ротаційно-поршневі гідромашини
- •Робоча рідина гідросистем і вимоги до неї
- •Поршневі компресори. Принцип дії, будова, класифікація
- •Основні параметри компресорів
- •Суміші ідеальних газів
- •Теплоємність, ентропія, ексергія
Тема «Сила тиску рідини на обмежувальні поверхні»
Чому дорівнює сила абсолютного гідростатичного тиску рідини на занурену в цю рідину плоску похилу поверхню?
Згідно з основним законом гідростатики ця сила визначається як добуток тиску в точці на значення площі поверхні, формула :
dР = рdF, де р — тиск у точці на глибині h.
P = (p0 + ρghc)F
Таким чином, сила абсолютного гідростатичного тиску рідини на занурену в цю рідину плоску похилу поверхню дорівнює добутку змоченої площі цієї поверхні на тиск у її центрі тяжіння.
Сформулюйте гідростатичний парадокс?
Коли сили тиску на дно посудин однакові при однакових площинах дна F, густинах рідин ρі глибинах hу посудинах. Але вага рідини в ємностях і реакції опор R, на які опираються посудини, будуть різні. Це явище прийнято називати гідростатичним парадоксом.
Чому дорівнює сили тиску на криволінійну поверхню?
Щоб визначити силу Рх, необхідно проінтегруватп dРх по поверхні аbсd:

де h1C – глибина занурення центра тяжіння під шар рідини,
Fyz – проекція поверхні аbсd на координатну площину уОz.
Таким самим шляхом можна визначити другу горизонтальну складову :
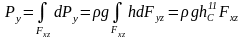
Що стосується вертикальної складової, то вона буде :
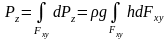
Але
інтеграл
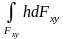 є не що інше, як об’єм призми abcda1b1c1d1
з
вертикальною твірною, обмеженою знизу
самою криволінійною поверхнею abcd,
а згори її проекцією Fхy
на площину вільної поверхні рідини. Як
наслідок цього :
є не що інше, як об’єм призми abcda1b1c1d1
з
вертикальною твірною, обмеженою знизу
самою криволінійною поверхнею abcd,
а згори її проекцією Fхy
на площину вільної поверхні рідини. Як
наслідок цього :
Pz = ρgV =G
де V — об'єм, G — вага рідини в об'ємі призми.
Тема «Закон Архімеда. Основи плавання тіл»
Сформулюйте закон Архімеда.
На занурене у рідину тіло діє вертикально спрямована вгору сила, що дорівнює вазі рідини в об'ємі тіла. У шкільних підручниках це формулюється так: на занурене у рідину тіло діє сила виштовхування, спрямована вгору і рівна вазі рідини виштовхнутої цим тілом.
Дайте визначення остійності.
Властивість тіла поновлювати початкове положення називається остійністю.
Дайте визначення метацентричної висоти.
Різниця між цими величинами називається метацентричною висотою:
hм = rм - е
Тема «Відносний спокій рідини»
Дайте визначення відносного спокою.
Відносним називається спокій, коли рідина перебуває у етапі спокою відносно певної системи, яка рухається у просторі.
2.Що розуміють під рідиною?
Під рідиною (у даному випадку) розуміємо систему матеріальних частинок, які утворюють безперервну суцільну масу, форми якої змінюються кожної миті.
3. В якому випадку рух рідини повністю визначений ?
Якщо в кожній точці нерухомого простору знаходиться рухома рідина, швидкість якої не залежить від часу і залишається постійною на протязі всього часу руху рідини, то рух називають усталеним.
Тема «Основні рівняння гідродинаміки»
Що виражає з енергетичної точки зору рівняння Бернуллі?
З енергетичної точки зору рівняння Бернуллі виражає закон збереження енергії, який формулюється так: енергія не виникає і не зникає, а перетворюється із однієї форми в іншу, і якщо в одному місці вона зменшується (збільшується), то в іншому на стільки, і тільки на стільки вона збільшується (зменшується).Таким чином, для замкненої системи енергія е незмінною, сталою величиною.
Як формулюється Бернуллі для потоку реальної рідини?
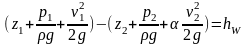 (3.13)
(3.13)
і формулюється так: різниця сум трьох напорів (геометричного, п'єзометричного і швидкісного), визначених для двох перерізів потоку реальної рідини, дорівнює величині напору, що губиться на подолання опорів під час руху рідини між вибраними перерізами.
В яких випадках застосовується рівняння Бернуллі?
Рівняння Бернуллі широко використовується в лабораторній і інженерній практиці при вирішенні ряду гідромеханічних задач: при гідравлічних розрахунках напірних трубопроводів, насосних установок, гідравлічних машин, центрифуг, сепараторів тощо.
Тема « Гідравлічні опори»
Скільки видів загальних втрат напору існує?
Загальні втрати напору hw бувають двох видів — по довжині hℓ і на місцевих опорах hr .
З чим пов'язане виникнення гідравлічних втрат напору під час руху реальної рідини?
Виникнення гідравлічних втрат напору під час руху реальної рідини пов'язані з роботою сил тертя у самій рідині, які характеризуються динамічною в'язкістю μ.
Наведіть формулу, за якою визначають загальні втрати напору hw.
У загальному випадку, коли мають місце два види опорів і відповідні їм втрати напору, то hw = Σ hℓ +Σ hr де Σ hℓ — сума втрат напору по довжині, — Σ hr сума місцевих втрат напору.
Загальні відомості про гідравлічні розрахунки трубопроводів
Охарактеризуйте прості та складні трубопроводи.
Простим називається трубопровід з постійним діаметром без бокових відгалужень по шляху руху рідини. Такий трубопровід може складатися з труб різного діаметра. Цей випадок є прикладом послідовного сполучення трубопроводів. Складний трубопровід можна розглядати як сукупність простих трубопроводів сполучених між собою послідовно, паралельно чи змішано.
Охарактеризуйте довгі та короткі трубопроводи.
До коротких трубопроводів відносяться такі, в яких місцеві втрати напору співмірні за значенням із втратами напору по довжині. При розрахунках таких трубопроводів визначаємо як втрати напору по довжині, так і на місцевих опорах. Довжина коротких трубопроводів рідко перевищує 50 м.
За допомогою якого рівняння виконується гідравлічний розрахунок простих коротких трубопроводів?
Швидкість рідини у трубопроводі vтр і витрати Q при інших відомих величинах можна визначити із формул:
 (5.6)
(5.6)
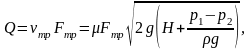 (5.7)
(5.7)
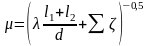 -
коефіцієнт
витрат трубопроводу.
-
коефіцієнт
витрат трубопроводу.
Для випадку коли р1 = р2, рівняння (5.5) набуває наступного вигляду :
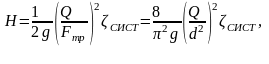
Звідки
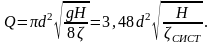
Запобігання гідравлічного удару
1.Охарактеризуйте прості та складні трубопроводи.
Простим називається трубопровід з постійним діаметром без бокових відгалужень по шляху руху рідини. Такий трубопровід може складатися з труб різного діаметра. Цей випадок є прикладом послідовного сполучення трубопроводів. Складний трубопровід можна розглядати як сукупність простих трубопроводів сполучених між собою послідовно, паралельно чи змішано.
2.Охарактеризуйте довгі та короткі трубопроводи.
До коротких трубопроводів відносяться такі, в яких місцеві втрати напору співмірні за значенням із втратами напору по довжині. При розрахунках таких трубопроводів визначаємо як втрати напору по довжині, так і на місцевих опорах. Довжина коротких трубопроводів рідко перевищує 50 м.
3.За допомогою якого рівняння виконується гідравлічний розрахунок простих коротких трубопроводів?
Швидкість рідини у трубопроводі vтр і витрати Q при інших відомих величинах можна визначити із формул:
(5.6)
(5.7)
- коефіцієнт витрат трубопроводу.
Для випадку коли р1 = р2, рівняння (5.5) набуває наступного вигляду :
Звідки
Три типи лопатей робочого колеса насоса
Охарактеризуйте типи лопатей робочих колес.
Н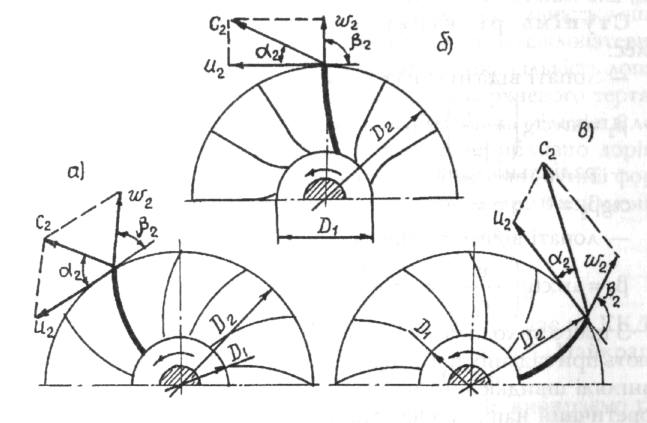 апрямок
струменя залежить від кутів
α2,
β2
і характеризується їх значеннями.
апрямок
струменя залежить від кутів
α2,
β2
і характеризується їх значеннями.
Теоретичний напір Нт залежить від кутів α 2 , β2.
Рис. 6.7. Типи лопатей робочого колеса: а - відігнуті назад, б - радіальні, в - зігнуті вперед.
Порівняємо теоретичні напори, створені робочими колесами з лопатями відігнутими назад, радіальними лопатями і лопатями зігнутими вперед (рис. 6.7).
Для лопатей відігнутих назад (рис. 6.7,а):
β2 < 900 ↔ ctg β2 > 0↔ HT< u22/g ;
для радіальних лопатей (рис. 6.7,б):
β2 = 900 ↔ ctg β2 = 0↔ HT = u22/g ;
для лопатей зігнутих вперед (рис. 6.7,в):
β2 > 900 ↔ ctg β2 < 0↔ HT> u22/g ;
Яким типом робочих колес створюється найбільший теоретичний напір?
Найбільший теоретичний напір створюється робочим колесом з лопатями зігнутими вперед, найменший -з лопатями відігнутими назад. Робоче колесо з радіальними лопатями створює середній теоретичний напір. На практиці використовуються виключно насоси з робочими колесами, в яких лопаті відігнуті назад. Такі колеса створюють менший теоретичний напір порівнянне з колесами, в яких лопаті відігнуті вперед, але мають більш високий гідравлічний ККД.
Підбір відцентрового насоса за заданими робочими параметрами
Що необхідно знати для вибору відцентрового насоса?
Для вибору відцентрового насоса необхідно знати також його призначення і характер змін подачі і напору у процесі перекачування рідини. За своїми конструктивними властивостями насоси мають Q -Н характеристики різної крутизни: круті, похилі і середньої крутизни.
2.Що застосовують приводами відцентрових насосів?
Приводами відцентрових насосів бувають синхронні і асинхронні електродвигуни. Частота обертання ротора синхронного двигуна nс кратна частоті електричного струму в мережі, до якої приєднаний двигун ns = 60f/р, де f - частота струму в мережі, р - кількість пар полюсів електродвигуна.
3. Чи суттєво відрізняються характеристики насосів при перекачуванні в'язких рідин від таких, що наводяться в довідковій літературі, отриманих при роботі насоса на воді?
При перекачуванні відцентровими насосами рідин з в'язкістю, що перевищує в'язкість води (ν > 10~6 м2/с), спостерігається збільшення опору тертя в проточній частині насоса. Тому подача і напір, створені насосом, зменшуються. При цьому зменшується і ККД насоса, при зростанні споживаної потужності. Внаслідок перерахованого, характеристики насосів при перекачуванні в'язких рідин суттєво відрізняються від таких, що наводяться в довідковій літературі, отриманих при роботі насоса на воді.
Нерівномірність подачі. Побудова графіків подачі
1.Який метод використовують для визначення ступеня нерівномірності подачі Qmах/Qсер поршневими насосами?
Що графічно визначає подачу насоса одинарної дії?
Перетин відповідних горизонталей і вертикалей дає точки 1' , 2', 3', 4', 5', які належать синусоїді. Визначимо площу між віссю абсцис і синусоїдою. Як видно із графіка висота безмежно малого прямокутника з основою dφ дорівнює ρsinφ , чи що теж саме FRsinφ. Площа цього елементарного прямокутника визначається добутком FRsinφdφ, тобто такою ж величиною, як і елементарна подача поршневого насоса із залежності . Таким чином, площа синусоїди графічно визначає подачу насоса одинарної дії.
За яким відношенням визначається ступінь нерівномірності подачі насоса подвійної дії ?
Для визначення середньої подачі насосу подвійної дії будуємо прямокутник, рівновеликий площам двох синусоїд. У цьому випадку 2πm = 2Fs = 4FR, а висота прямокутника становить m = 2FR/π. Ступінь нерівномірності подачі насоса подвійної дії визначається відношенням:

