6 Билет

1.SCADA типті жүйелердің жалпылама құрылымы. Автоматтандырылған басқару жүйелеріндегі (SCADA-жүйелердегі)  ақпаратты жинауды ұйымдастыру жалпы жұмыс істеу алгоритміне сәйкес (ШУЖ циклограммасы, 2 дәріс) технологиялық басқару объектісінің (ТБО) технологиялық айнымалылар датчиктерінен  ақпаратты цифрлық формада алуды анықтайды (3.1 суретті қара).

 

 

 

 

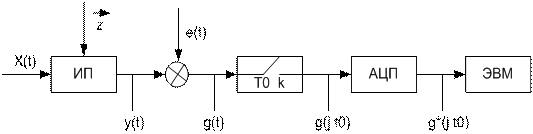
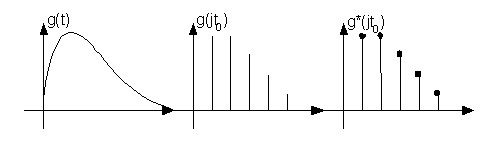
                3.1 сурет- Ақпаратты жинауды ұйымдастыру сұлбасы

x(t) – өлшенетін ақпарат сигналы

g(t) – түрлендіргіштің шығыс шамасы (пайдалы сигнал)

z – әсер етуші факторлар

g(t) – пайдалы сигнал және бөгеуілдің қоспасы

к – коммутатор

Температураны термопарамен өлшеген кездегі Х айнымалысын іске асыру мысалы:

                 

 

мұндағы:

t – ыстық дәнекер температурасы – x

t0 – суық дәнекер температурасы z0.

  

Егер  z0    - номинальді статикалық сипаттама

 

Ары қарай деңгей бойынша кванттау нәтижесінде y*(j t0) аламыз.

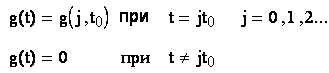
Ақпаратты бастапқы өңдеу. ЭЕМ-де параметрдің сандық мәнінде сақталатын алгоритмдер тобы ақпаратты бастапқы өңдеу алгоритмдері деп аталады. Ақпаратты бастапқы өңдеудің  негізгі алгоритмдері:

1)     Ақпараттың анықтылығын бақылау.2)     Интерполяция және экстраполяция. 3)     Өлшенетін ақпараттың сигналдарын фильтрациялау. 4)     Датчиктерді аналитикалық градуирлеу. 5)     Қалпына келтірілген мәндерді түзету.

Ақпараттың анықтылығын бақылау.Ең жиі кездесетін ақпараттың анықты емес себептері келесідей:

1)     датчиктердің және түрлендіргіштердің ақаулығы; 2)     байланыс линияларындағы бөгеуілдердің әсері;

3)     өлшеу приборларының метологиялық сипаттамаларының нашарлауы.

2.Систематикалық код. Егер A_ki =  вектор-жолын M_n,k = [ I_k P_k,n-k ] матрицасына көбейтсек, A_n,i = векторын аламыз, мұндағы  тексеруші символдары ақпараттық символдардың сызықты комбинациялары болып табылады:

               (10.2)

Мұндай шартқа жауап беретін кодаларды сис­тематикалық деп атайды. Әрбір сызықты код үшін эквивалентті систематикалық код бар болады. Өз кезегінде, берілген P_k,n-k  қосымша-матрица бойынша коданы құру ережелерін беретін теңдіктерді анықтауға болады. Әрбір бағанның бірінші жолындағы бірлік, бағанға сәйкес тексеруші разрядтың құрылуына бірінші ақпараттық разряд қатысқандығын көрсетеді. Кез келген бағанның келесі жолындағы бірлік тексеруші разрядты құрауға екінші ақпараттық разрядтың қатысатындығын көрсетеді және т.с.с. Қосымша-матрица коданы құру ережелері туралы барлық ақпараттан тұратындықтан, берілген қасиетпен систематикалық кодты сәйкес  қосымша-матрицаны құру жолымен синтездеуге болады. Сызықты коданың  d ең кіші кодтық ара қашықтығы оның нөлдік емес векторларының ең кіші салмағына тең болатындықтан, қосымша-матрицаға келесі жалпы шартқа қанағаттандыратын k жолдар қосылуы керек: кез келген  l(1≤l≤k) жолдарды қосу кезінде алынатын құраушы матрицаның вектор-жолында    d — l-ден кем емес нөлден ерекше символдар болуы керек. Расында да, көрсетілген шарт орындалған кезде құраушы матрицаның l жолдарын қосумен алынған кез келген рұқсат етілген кодты комбинацияда       d-дан кем емес нөлдік емес символдар болады, өйткені онда бірлік матрицаның жолдарын қосу нәтижесінде әрқашан  l  нөлдік емес символдар болады. Осындай жолмен d = 3 ең кіші кодтық ара қашықтықпен (7,4) екілік систематикалық коданың құраушы матрицасын синтездейік. Тұжырымдалған шартқа сәйкес қосымша-матрицаның әрбір вектор- жолында (l = 1 кезінде) екі бірліктен кем болмауцы керек. Үш разрядты векторлардың арасында мұндайдан төртеу бар: 011, 110, 101, 111.

Бұл векторлар бірлік матрицаның жолдарымен кез келген ретте салыстырылуы мүмкін. Нәтижесінде Хэмминг кодына эквивалентті систематикалық кодалардың матрицасын аламыз, мысалы:

                               M_7,4   = .

Мұндай матрицаның бірнеше жолдарын қосқан кезде (l>1) d = 3-ден кем емес нөлдік емес символдары вектор-жол алатындығымызға көз жеткізу күрделі емес.

3. Қателер қорабын табу және түзету. . Символ дар тізбектерінде қателер тәуелсіз пайда болатын каналдарда қолданылатын маңызды кодалар класы болып Боуз – Чоудхури – Хоквингем кодалары табылды. Т ж/е s<n/2 кез келген бүтін оң сандары үшін, 2s еселікті қателерді табуға немесе s еселікті қателерді түзетуге қабілетті, тексеру символдарының саны ms-тен аспайтын n=2^T-1 ұзындықты бұлкластың екілік коды бар екендігі дәлелденген. Бұл кодалардың теориялық аспектрлерін түсіну үшін жоғары алгебраның бірқатар жаңа түсіністерімен танысу керек.

Қателер қорабын табу және түзету. b немесе одан кем ұзындықты қателер қорабын түзетуге негізделген ерікті сызықты блоктық (n,k)-код үшін, түзетушілік қабілетті артық символдар санымен байланысты орнататын негізгі қатынас болып Рейджер шекарасы табылады: n-k≥2b, (13.1). l≥b немесе одан кем ұзындықты пакеттерді бір уақытта табумен b немесе одан кем ұзындықты пакеттерді сызықты кодпен түзету кезінде ең болмағанда b+1 тексеруші символдар қажет. Қателер қорабын түзетуге арналған циклдық кодалардан Бартон, Файр жәнеРид – Соломон кодалары кеңінен танымал. Кодалардың бастапқы екі түрі блоктағы бір қателер қорабын түзету үшін қызмет атқарады. Рид-Соломон кодалары бірнеше қателер қорабын түзетуге қабілетті.