шығыс

3 Сурет - Кері байланысты қосқышпен циклды код кодерінің сұлбасы

кіріс

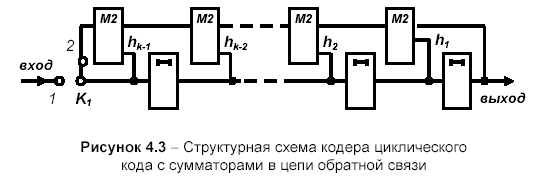
Жады ұяшықтарының шығысы кері байланыс сумматорына генераторлық көпмүше

түріне сәйкес қосылады. Бастапқы жағдайда К1 кілті 1 жағдайда болады. Бірінші к такт ішінде кірістегі ақпараттық символдар регистрдің барлық ұяшықтарын толтырады. Одан кейін кілтті 2 жағдайға ауыстырады. Әрбір келесі такттерде байланыс каналына ақпараттық символдың біреуі беріледі және регистрдің соңғы ұяшығына жазылатын тексеру символы қалыптасады. n-k тактіден соң тексеру символын қалыптастыру аяқталады да К1 кілті қайтадан 1 жағдайға ауысады.

3.Негізгі алгебралық жүйелер. Топтар. Кейбір алгебралық операциялар анықталған жиындарды алгебралық жүйелер деп атайды. Алгебралық операция деп белгілі ережелер бойынша кейбір үшінші элементті екі элементке бір мағыналы салыстыруды түсінеді. Әдетте негізгі операцияны тіпті бұл операциялар сандарға орындалмаса да және сәйкес арифметикалық операцияларға ұқсас емес болса да қосу (а+b = с деп белгілейді) немесе көбейту (а∙b = с деп белгілейді), ал оған кері - алу немесе бөлу деп атайды.

Түзетуші кодалар теориясында кеңінен қолданылатын негізгі алгебралық жүйелерді қысқаша қарастырайық. Топ деп, бір негізгі операция анықталған және келесі аксиомалар орындылатын элементтер жиынын айтады:

1) Топтың кез келген екі элементіне операцияны қолдану нәтижесінде осы топтың элементі түзіледі (тұйықтылық талабы). 2) Топтың кез келген a, b және с элементтері үшін (а+b)+c = а+(b+c) теңдігі (егер негізгі операция - қосу) және a∙(bc) = (ab)∙c теңдігі (егер негізгі операция – көбейту) қанағаттандырылады. 3) Кез келген Gn тобында Gn –нен a-ның кез келген мәндерінде a+0=0 + a = a шартына (егер негізгі операция – қосу) немесе шартты түрде a • 1 = 1 • а = а (егер негізгі операция – көбейту) қанағаттандыратын бір мағыналы анықталған элемент бар. Бірінші жағдайда элемент нөл деп аталады және 0 символымен белгілейді, ал екінші жағдайда - бір деп аталады 1 символымен белгілейді. 4) Топтың кез келген а элементінде а + (— а) = — а+ а = 0 теңдеуімен (егер негізгі операция - қосу) немесе • a-1 = a-1• a= 1 теңдеуімен (егер негізгі операция – көбейту) бір мағыналы анықталған элемент бар.

Бірінші жағдайда бұл элементті қарама-қарсы деп атайды және (-а) деп белгілейді, ал екінші жағдайда - кері деп атайды және a-1 деп белгілейді.

Егер топта анықталған элемент коммутативті болса, демек a +b = b + a (қосу бойынша топ үшін) немесе a • b = b • a теңдігі (көбейту бойынша топ үшін) әділ болса, онда топты коммутативті немесе абельдік деп атайды.

Шекті элементтер санынан тұратын топты шекті деп атайды. Топтағы элементтер санын топтың реті деп атайды.

Бізбен қарастырылатын n-разрядты кодты комбинациялар жиыны шекті топ болуы үшін, негізгі операцияны орындау кезінде нәтижелік кодты комбинациядағы разрядтар саны артпауы керек. Бұл шартқа, топ элементтерінің бірдей разрядтарының цифрлары әдеттегі ретпен қосылатын, ал қосу нәтижесі болып алынған санды q модуліне бөлгендегі қалдық саналатын берілген q модулі бойынша (q – жай сан) символикалық разряд бойынша қосу операциясы қанағаттандырады.