1 Билет

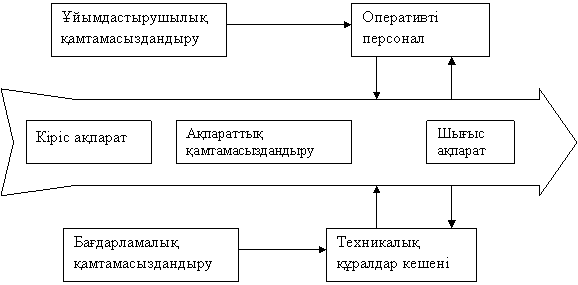
1.ТПАБЖ тағайындалуы және ұйымдастырылуы. Таратылған ТПАБЖ-і ТПАБЖ- адам шешім шығаруға мағыналы қатысатын адам-машиналық жүйе. ТПАБЖ, объектіге әрекетті ондағы өтетін процестер түрінде жасайды, демек ТПАБЖ шынайы уақыт режімінде жұмыс істейді. ТПАБЖ-де объекті ретінде технологиялық басқару объектіісі қарастырылады.Технологиялық басқару объектіісі, технологиялық құрылғылар мен онда сәйкес нұсқаулықтар  мен регламенттер  бойынша іске асырылатын мақсатты өнімді өндірудің технологиялық процесінің  жиынтығы болып табылады. ТПАБЖ-де технологиялық басқару объектісі ретінде технологиялық қондырғылар, барлық кәсіпорынның бөлек өндірістері мен технологиялық процестері қарастырылады. ТПАБЖ-ны құру кезінде бұл жүйенің мақсатын анықтау керек. Қойылған мақсатқа жету дәрежесін басқару критерийлері көмегімен сипаттау қабылданған.

ТПАБЖ құрамы 1.1 суретте берілген.

 

 

 

 

 

 

 

 

 

 

 

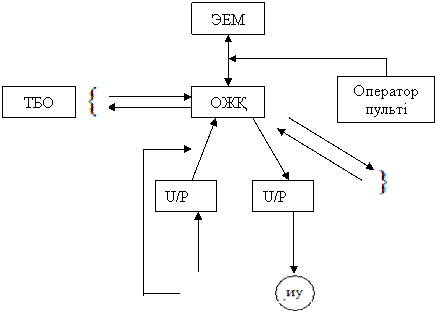
Оперативті персонал, объектті бақылау мен басқару жасайтын оператор-технологтардан және жүйенің техникалық құралдарының қызмет етуін қамтамасыз ететін эксплуатациялық персоналдан тұрады. Ұйымдастырушылық қамтамасыз ету, оперативті персоналдың қызмет ету тәртібі мен  ережелерін орнататын құжаттар жиынтығы болып табылады. Оларға процесті қалыпты, апат алды және апатты жағдайларда жүргізуді анықтайтын технологиялық нұсқаулықтар мен регламенттер мен жүйені пайдалану бойынша нұсқаулықтар жатады.Бағдарламалық қамтамасыздандыру құрамына операциялық жүйе, мәліметтер базаларын басқару жүйесі (МББЖ) және арнайы бағдарламалық қамтамасыздандыру кіреді.ТПАБЖ-н құрылымдық ұйымдастыру. Орталықтандырылған ТПАБЖ (1.2 суретті қара)

 

 

 

 

 

 

 

                       

1.2 Сурет – Технологиялық объектті басқаруды орталықтандырылған басқару жүйесі

Объектпен байланыс құрылғысы (ОБҚ) құрамына АЦТ (аналогты-цифрлық түрлендіргіш); ЦАТ (цифрлық-аналогты түрлендіргіш) және коммутатор кіреді. Оның кемшіліктеріне датчиктерді объектпен байланыстыратын көптеген электр сымдарының болуын және ЭЕМ-нің істен шығуын жатқызуға болады (көп резервтер).

Таратылған ТПАБЖ-і Таратылған ТПАБЖ мысалы 1.3 суретте көрсетілген.

 

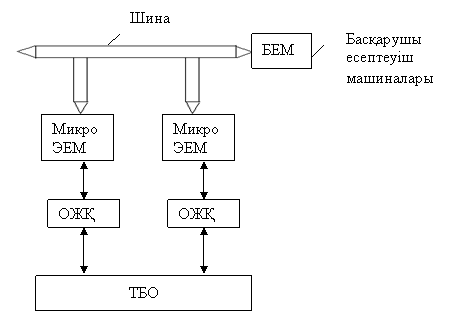
1.3  сурет - Технологиялық басқару объектісінің таратылған басқару жүйесі

     Цифрлық датчиктердің пайда болуымен тек қана ақпаратты цифрлық формада өңдеу мүмкіндігі ғана емес, сондай ақ бұл ақпаратты цифрлық түрде тасымалдау мүмкіндігі де пайда болды. Бөлек құрылғылардың арасында мәліметтерді цифрлық тасымалдау АБЖ-н құру негізі ретінде есептеу торабын жасады. Мұндай есептеу торабы үлкен емес аумақта орналасқан қолданушылар үшін резервтерді құру үшін қолданылады, сондықтан мұндай торап жергілікті деп аталады.

Қазіргі кезде 2 типті таратылған басқару жүйелерін ерекшелейді:1 – SCADA-жүйелер;2- DCS-жүйелер;

SCADA – Supervisory Control and Data Acquisition – мәліметтерді жинау және басқару жүйесі;

         DCS – Distributed Control System – децентрализацияланған басқару жүйелері.

2.Қалынды. Идеалдың түзуші көпмүшесі. Модулі екі бойынша ұқсас мүшелерді келтірумен кәдімгі ережелер бойынша көпмүшелерді көбейту операциясы тұйықтылық шартының бұзылуына әкелуі мүмкін екендігін көру күрделі емес. Расында да, көбейту нәтижесінде n—1-ден жоғарырақ дәрежелі, 2(n— 1)-ге шейін көпмүшелер алуынуы мүмкін, ал оларға сәйкес кодтық комбинацияларда  n-нен асатын разрядтар саны болады, демек, қарастырылатын жиынға жатпайды. Сондықтан символикалық көбейту операциясы былай беріледі:1) көпмүшелер кәдімгі ережелер бойынша, бірақ ұқсас мүшелерді модулі екі бойынша келтірумен көбейтіледі; 2) егер көбейтудің үлкен дәрежесі  n—1-ден аспаса, онда ол символикалық көбейту нәтижесі болып табылады; 3)      егер көбейтудің үлкен дәрежесі n-нен үлкен немесе тең болса, онда көбейтудің көпмүшесі алдын ала анықталған n дәрежелі көпмүшеге бөлінеді де символикалық көбейту нәтижесі болып бөлгендегі қалдық есептеледі.

  Қалдықтың дәрежесі n—1-ден аспайды, демек, бұл көпмүше n - разрядты кодты комбинациялардың жиынына тиісті. Кодты комбинацияның соңына бірлікті тасымалдаумен циклдық жылжытуды талдау кезінде мұндай  n-ші дәрежелі көпмүше болып х^п+1 көпмүшесі табылады.

Расында да, n — 1 дәрежелі көпмүшені на х-ке көбейту нәтижесінде алатынымыз

                      G(x) = (x^{n- 1}+ x^{n- 2}+…+ x+1)∙x = xⁿ+ x^{n- 1}+…+ x                      (11.2

Демек, көбейту нәтижесі бастапқы кодты комбинацияны циклдық жылжыту жолымен құрылатын кодты комбинацияға сәйкес болуы үшін, онда хⁿ  1-ге ауыстыру қажет. Мұндай ауыстыру көбейту кезінде алынған көпмүшені хⁿ+1-ге, нәтиже ретінде, бөлгендегі қалдықты жазумен бөлуге эквивалентті. Әдетте оны қалдықды алу немесе модулі х^п+1 бойынша келтіру деп атайды (қалдықтың өзін бұл кезде қалынды деп атайды). Енді біздің сақинада g(x) көпмүшесіне еселікті барлық көпмүшелердің ішкі жиынын ерекшелейік. Мұндай ішкі жиынды идеал, ал g(x) көпмүшесін — идеалдың туғызушы көпмүшесі  деп атайды. Идеалдағы әртүрлі элементтердің саны оның туғызушы көпмүшесінің түрімен анықталады. Егер туғызушы көпмүше ретінде 0-ді алса, онда барлық идеалды тек қана осы көпмүше құрайтын болады, өйткені оны кез келген басқа көпмүшеге көбейту 0-ді береді. Егер туғызушы көпмүше ретінде 1 қабылданса [g(x) =1], онда идеалға сақинаның барлық көпмүшелері кіреді. Жалпы жағдайда, n—k дәрежелі қарапайым көпмүшемен туғызылған идеалдың элементтер саны 2^k құрайды. Енді n-разрядты екілік кодты комбинациялардың сақинасында бізбен құрылған циклдық екілік коданың идеал болып табылатындығы түсінікті болады.

3. Циклды кодты түзу әдістері. Кез келген (n, k) топтық коды n символдан k сызықты тәуелсіз жолдан тұратын матрица түрінде жазыла алады және керісінше, кез келген жиынтық k сызықты тәуелсіз n-разрядты кодты комбинациялар жиынтығы кейбір топтық коданың құраушы матрицасы ретінде қарастырылы алады. Мұндай кодалардың барлық алуан түрлілігінің арасында, құраушы матрицаларының жолдары циклдықтың қосымша шартымен байланысқан кодаларды ерекшелеуге болады. Мұндай коданың құраушы матрицасының барлық жолдары, берілген код үшін құраушы деп аталатын бір комбинацияны циклдық жылжытумен алынуы мүмкін. Бұл шартқа қанағаттандыратын кодалар циклдық кодалар деген атқа ие болды.

Жылжыту оңнан солға қарай жасалады, әрі шеткі сол жақтағы символ әр кезде комбинацияның соңына ауыстырылады. Мысалы, 001011 комбинациясын циклдық жылжытумен алынатын кодты комбинациялар жиынтығын жазайық:

G = .

Мүмкін болатын циклдық ( n, k )-кодалардың саны әртүрлі топтық (n, k)-кодалардың санынан едәуір аз.

Мысалы, көпмүше түрінде 01011 түзуші кодалық комбинацияны жазайық:

G(x) = 0 • х4 + 1 • х3 + 0 • х2 + 1 •х + 1 .

Көпмүшені жазған кезде нөлдік коэффициенттермен мүшелер жазылмайтындықтан, түзуші көпмүше:

G(x) = x3 + x+1. (11.1)

Нөлдік емес коэффициентпен қосылғыштағы х-тің ең үлкен дәрежесін көпмүшенің дәрежесі деп атайды. Енді кодты комбинациялармен әрекеттер көпмүшелермен әрекеттерге әкелінеді. Көпмүшелерді қосу коэффициенттерді модулі екі бойынша келтірумен жасалады. Кодтық комбинацияның соңына бірлікті тасымалдаусыз n — k дәрежелі кейбір құраушы көпмүшені көрсетілген циклдық жылжыту қарапайым х-ке көбейтуге сәйкес келеді. Мысалы, go(x) =x3+х+1 көпмүшесіне сәйкес келетін матрицаның бірінші жолын (001011) х-ке көбейтіп, x∙go(x) көпмүшесіне сәйкес келетін матрицаның екінші жолын (010110) аламыз.

Бұл екі комбинацияларды қосу кезінде алынатын кодты комбинация да

х3 + х+1 көпмүшесін х+1 көпмүшесіне көбейту нәтижесіне сәйкес болатындығына көз жеткізу күрделі емес. Расында да,

0 0 1 0 1 1 х3 + 0 + х +1

0 1 0 1 1 0 x +1

0 1 1 1 0 1 х3 + 0 + х + 1

х4 + 0 + х2 + x

х4 + х3 + х2 + 0 +1.

Үлкен (n-ші) разрядта (сол жақта) бірлікпен матрицаның жолын циклдық жылжыту жолға сәйкес көпмүшені х-ке нәтижеден хn +1 = хn— 1 көпмүшесін бір уақытта алып тастаумен, демек, модулі хn + 1 бойынша келтірумен көбейтуге тепе-тең.