6. Нахождение оси гидравлического прыжка

Решение производится графическим способом. Сначала строим так называемую кривую сопряженных глубин 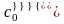воображаемого гидравлического прыжка.

Для прямоугольного сечения потока сопряженные глубины (большая h” и меньшая h’) определяются по формулам:

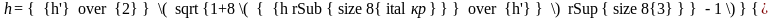(6.1)

(6.2)

В данном случае меньшие сопряженные глубины h’ берутся с кривой подпора с₀.

Гидравлический прыжок условно изображается в виде вертикальной линии, начинающейся от точки пересечения кривых b₀ и . На этой линии глубины, определяемые кривой подпора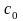 и кривой спада b₀, будут сопряженными.

С чертежа получены сопряженные глубины до прыжка и после прыжка:

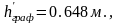
В качестве проверки определим теоретически большую сопряженную глубину и сопоставим ее с глубиной 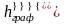,найденной графическим способом. Найдем по зависимости (6.1), подставив глубину , снятую с чертежа

Расхождение в % между глубиной и устанавливают по формуле

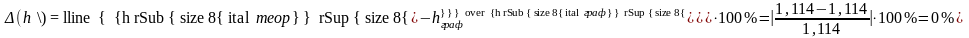
Расхождение 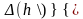= 0% считаем допустимым (меньше 5%).

7. Потери энергии в прыжке.

Затраты энергии (или потерянный напор) в гидравлическом прыжке для русел прямоугольного сечения определяют по формуле

Где 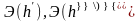- значение удельной энергии сечения соответственно перед прыжком и за прыжком .

8. Построение кривой свободной поверхности на наклонном участке канала.

На наклонном участке канала строим кривую спада b₂, начиная от точки перелома дна с глубиной h_пер = h_кр до нормальной глубины h_02. Под глубиной на наклонном участке понимается расстояние от дна до свободной поверхности потока по вертикали.

Алгоритм построения кривой спада b₂ сохраняет все черты построения кривой подпора c₀ в п.5.1, с той разницей, что здесь кривая свободной поверхности асимптотически приближается (сверху) к линии нормальных глубин N-N и в качестве конечной расчетной глубины принимается

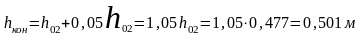
Таким образом, если длина наклонного участка канала достаточно велика, то тогда кривая спада b₂ может практически достичь нормальной глубины h₀₂ и далее вниз по течению будет равномерное движение жидкости. Если длина наклонного участка не велика, то кривая b₂ может не достичь нормальной глубины в пределах этого участка, и здесь равномерное движение не установится.

H1 H2 L SUM

0.860 0.821 0.158 0.158

0.821 0.782 0.530 0.689

0.782 0.743 1.011 1.699

0.743 0.704 1.646 3.345

0.704 0.665 2.517 5.862

0.665 0.626 3.764 9.627

0.626 0.587 5.671 15.297

0.587 0.548 8.888 24.185

0.548 0.509 15.354 39.539

0.509 0.470 35.011 74.550

Заключение

В существующей учебной литературе по речной гидравлике большой объем материала отводится изложению приближенных и трудоемких методов интегрирования дифференциального уравнения неравномерного движения в открытых руслах.

В данной курсовой работе дано решение характерного примера по построению кривых свободной поверхности в призматических руслах с применением численных методов на ЭВМ.

Применение ЭВМ для построения кривых свободной поверхности дает возможность отказаться от трудоемких приближенных методов, и делает расчет достаточно простым, точным и не трудоемким.