2.4 Определение глубины в сжатом сечении

Для канала прямоугольного сечения глубина в сжатом сечении определяется по формуле:

h_c=ɛ* h_щ=0.71*0.52=0.369

Сжатое сечение с-с находится в непосредственной близости от щита.

3.Численное интегрирование основного дифференциального уравнения неравномерного движения в призматическом русле

Расчет кривых свободной поверхности на участках канала прежде всего заключается в определении расстояния между сечениями потока, глубины которые известны, что должно в итоге обеспечить нахождение глубины потока в любом сечении, отстоящим на заданном расстоянии от какого-либо начального сечения.

В данной работе нахождение расстояния между сечениями с глубинами и основано на численном интегрировании основного дифференциального уравнения неравномерного движения:

Это дифференциальное уравнение преобразуют к виду, удобному для интегрирования

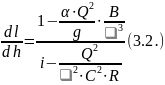
Т.к. гидравлические элементы потока являются функциями глубины , то для правой части уравнения (3.2) вводится обозначение

Тогда дифференциальное уравнение (3.2) запишется

После разделения переменных имеем

Интегрируя это дифференциальное уравнение между сечениями 1-1 (с глубиной ) и 2-2 (с глубиной ), расстояния которых от некоторого начального сечения равны соответственно , получим

или

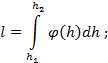(3.4)

где – расстояние между сечениями 1-1 и 2-2.

Для рассматриваемого здесь определенного интеграла точное аналитическое выражение для первообразной функции найти не удается. В этом случае прибегают к численному интегрированию, т.е. вычисление определенного интеграла проводят по так называемым квадратурным формулам (формулы трапеции, Симпсона, Гаусса и др.), в которые входят значения подынтегральной функции в конечном числе узлов, расположенных на отрезке . Одна из распространенных на практике квадратурных формул - формула Симпсона (формула парабол) используется в данной работе.

Формула Симпсона (в общепринятых в математике обозначениях):

,

y_i = f(x_i), x_i = a + ih, (i = 0,1,2,…,n), - шаг интегрирования (n – четное число).

4. Выявление форм кривых свободной поверхности потока на участках канала

При анализе форм движения потока воды на участках рассматриваемого канала важную роль играет образованное в непосредственной близости от щита сжатое сечение с–с с глубиной h_c.В сжатом сечении наблюдается наибольшая скорость течения и поток имеет наибольшую удельную кинетическую энергию, расходуемую затем на преодоление гидравлических сопротивлений по длине на участках канала.

Расстояние от щита до сжатого сечения (равно примерно высоте отверстия) обычно невелико по сравнению с длиной горизонтального участка. Поэтому в дальнейшем принимаем длину L₁ горизонтального участка, равной расстоянию от сжатого сечения с глубиной h_с до перелома дна канала с глубиной h_пер.

Оказывается, при заданных условиях, когда для расчетных значений глубин h_кр, h₀₂, h_с выполняются соотношения h_с < h₀₂< h_кр, формы свободной поверхности потока на обоих участках канала и наличие или отсутствие гидравлического прыжка самым существенным образом зависят от длины горизонтального участка, что усматривается на рисунках 1 – 6.

Как частный случай истечения из прямоугольного отверстия (истечения из-под щита) в канал с двумя участками на рисунке 1 представлен случай, когда горизонтальный участок имеет нулевую длину. Здесь сразу за сжатым сечением в пределах наклонного участка устанавливается кривая подпора с₂, в низовой части асимптотически приближающаяся (снизу) к линии нормальных глубин N-N. Отметим что, на наклонном участке канала движение жидкости осуществляется за счет кинетической энергии, запасенной в сжатом сечении, и работы силы тяжести жидкости.

Введем в рассмотрение критическую длину L_кр горизонтального участка, которую будем определять по формуле (3.4)

при h₁ = h_c, h₂ = h_кр. Далее проведем анализ возможных форм движения потока на участках канала уже в зависимости от условий L₁ ≤ L_кр. и L₁  L_кр,

На каждом из рисунков 2,3,4,5 представлена схема канала с “укороченным” горизонтальным участком, когда L₁ ≤ L_кр и запас кинетической энергии в сжатом сечении оказывается достаточным для пребывания потока в бурном состоянии (при глубинах h ≤ h_кр) на всем протяжении канала без образования гидравлического прыжка. В каждом из этих случаев, начиная от сжатого сечения вниз по течению, устанавливается кривая подпора с_о, которая распространяется по всей длине горизонтального участка.

Как известно, вид кривой свободной поверхности потока в пределах наклонного участка канала с уклоном дна, большим критического, определяется глубиной h_пер, с которой поток приходит к началу этого участка. Здесь могут быть следующие случаи.

1. (рис.2)

Кривой свободной поверхности в пределах наклонного участка канала будет кривая подпора с₂.

2. (рис.3)

На наклонном участке канала будет наблюдаться равномерное движение с глубиной h₀₂ по всей длине этого участка.

3. (рис.4)

Свободная поверхность потока на наклонном участке очерчена кривой спада b₂.

4. (рис.5)

Во–первых, из рисунка 5 усматриваем, что сечение потока с глубиной, равной критической глубине (h = h_пер = h_кр) совпадает с концевым сечением горизонтального участка. Таким образом, критическая длина L_кр представляет собой расстояние по горизонтали от сжатого сечения с глубиной h_с до сечения с глубиной h_кр и для кривой подпора с_о является наибольшей возможной. Во–вторых, на наклонном участке канала кривая свободной поверхности очерчена кривой b₂, асимптотически приближающейся к линии нормальных глубин N – N.

В данной работе численным интегрированием на ЭВМ найдена критическая длина горизонтального участка

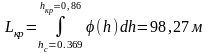
Здесь в выражении для подынтегральной функции

принято i = i₁ = 0.

В случае «удлиненного» горизонтального участка канала ), т.е. при превышении длины L₁ над критической длиной L_кр, запас кинетической энергии в сжатом сечении будет недостаточным для поддержания бурного состояния по всей длине участка. Поэтому на таком горизонтальном участке осуществляется переход потока из бурного состояния в спокойное посредством гидравлического прыжка.

Как известно, прыжок может быть затопленным, надвинутым и отогнанным. В данном задании принято

.

Такое задание длины L₁ обеспечивает здесь наличие отогнанного гидравлического прыжка, расположенного ниже по течению относительно сжатого сечения и разделяющего горизонтальный участок на допрыжковый и послепрыжковый части конечной длины.

При отогнанном гидравлическом прыжке кривая подпора с_о будет доходить только до начала прыжка. На послепрыжковой части горизонтального участка свободная поверхность потока будет очерчена кривой спада b_о с уменьшением глубины до критической.

При наличии отогнанного прыжка свободная поверхность потока на наклонном участке канала будет очерчена кривой спада b₂ (рис.6), начинающейся от водопада ( в верхней части участка сопрягающейся с кривой b_o ), и в низовой части - асимптотически приближающейся к линии нормальных глубин N – N.