2. Определение критических характеристик и гидравлических элементов потока

Гидравлический расчет потока при истечении из-под щита в канал с двумя участками сводится к определению критической глубины h_кр , нормальной глубины h₀₂ (на наклонном участке), реально существующей глубины 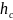в сжатом сечении потока, к анализу кривых свободной поверхности потока, определению типов этих кривых и их расчетов, то есть отысканию глубин в различных сечениях по длине участков.

2.1 Определение критической глубины потока

Глубина потока, при которой заданный расход Q проходит в данном сечении с минимальным запасом удельной энергии, называется критической глубиной.

Критическая глубина h_кр определяется из основного уравнения критического состояния потока:

(2.1.1)

где, – площадь живого сечения (для прямоугольного сечения ) при глубине, равной критической;

В– ширина русла по верху живого сечения при той же глубине(здесь В=b);

– ускорение свободного падения;

– коэффициент кинетической энергии (коэффициент Кориолиса), обычно принимаемый ;

–расход жидкости.

Из этого уравнения для русла прямоугольного сечения получаем искомую величину

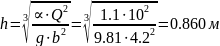
. Критическая глубина не зависит от уклона дна на участках канала и остается одинаковой на всем его протяжении. Пользуясь понятием критической глубины устанавливают состояние потока:

а) h > h_кр - спокойное состояние ;

б) h = h_кр - критическое состояние;

в) h < h_кр – бурное состояние.

Здесь h – действительная глубина потока.

2.2 Определение критического уклона для наклонного участка канала

Критическим уклоном называется такой уклон дна, при котором поток с заданным расходом Q проходит по каналу в условиях равномерного движения с глубиной, равной ,

Разрешая основное уравнение равномерного движения

относительно уклона, получим формулу

.

Здесь ω - площадь живого сечения;

– смоченный периметр;

–гидравлический радиус;

– коэффициент Шези, вычисляемый по формуле Маннинга.

При заданных в работе Q, b, n и найденной глубине h_кр = 0.86 м получено искомое значение критического уклона

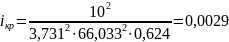
Сопоставление заданного уклона i_{2= 0,021} наклонного участка канала с критическим уклоном i_{кр = 0,0029} дает возможность убедиться в том, что .

2.3 Определение нормальных глубин на участках канала

Глубина, которая при заданном расходе Q установилась бы в русле, если бы в этом русле движение было равномерным, называется нормальной.

На горизонтальном участке, где , равномерного движения не может быть , поэтому нормальная глубина здесь отсутствует.

Для определения нормальной глубины h₀₂ на наклонном участке канала опять используем основное уравнение равномерного движения

Преобразуем это уравнение, подставив в функции от h выражения гидравлических элементов потока ω = b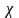h, = b + 2h, , .

Получаем

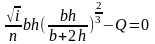(2.3.1)

В последнем уравнении, где неизвестной величиной является глубина h, надо принять

Имеем нелинейное уравнение вида

F(h) = 0 (2.3.2)

Уравнение (2.3.1) решаем численно – методом касательных (методом Ньютона).

Используем известную итерационную расчетную формулу

, (2.3.3)

k=0,1,2,… .

Для функции

найдена ее производная

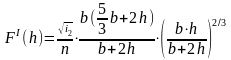
Поскольку величины нормальной и критической глубин соизмеримы, то в качестве начального значения h⁽⁰⁾ в процессе итераций удобно принять h⁽⁰⁾ = h_кр.

_{В результате счета на ЭВМ получаем} h_{02= 0,477 м. Как и следовало ожидать, при заданных в работе Q, b, n и выполняется неравенство (0,477м<0,860м).}