33. Среднеарифметическое значение измеренной величины и среднеквадратическая ошибка арифметической середины.

Арифметическая середина. Пусть имеется n измерений одной величины X, то-есть,

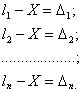Сложим эти равенства, суммарное уравнение разделим на n и получим:     Величина        называется средним арифметическим или простой арифметической серединой по третьему свойству ошибок можно написать: что означает, что при неограниченном возрастании количества измерений простая арифметическая середина стремится к истинному значению измеряемой величины. При ограниченном количестве измерений арифметическая середина является наиболее надежным и достоверным значением измеряемой величины.

Запишем формулу (1.36) в виде и подсчитаем среднюю квадратическую ошибку арифметической середины, которая обозначается буквой M. Согласно формуле (1.32) напишем:

Или Но ml1 = ml2 = ... = mln= m по условию задачи, так как величина X измеряется при одних и тех же условиях. Тогда в квадратных скобках будет n * m2, одно n сократится и в итоге получим: M2 = m2/n или     то-есть, средняя квадратическая ошибка арифметической середины в корень из n раз меньше ошибки одного измерения.Вычисление средней квадратической ошибки по уклонениям от арифметической середины. Формулу Гаусса (1.27) применяют лишь в теоретических выкладках и при исследованиях приборов и методов измерений, когда известно истинное значение измеряемой величины. На практике оно, как правило, неизвестно, и оценку точности выполняют по уклонениям от арифметической середины.

34. Определение отметки точки, расположенной между горизонтами аналитическим способом. Отметка – это высота точки местности над уровенной поверхностью. На рис. 2.1 показано построение горизонталей на небольшом участке, для которого уровенную поверхность можно принять за плоскость. Здесь секущие плоскости Р₁,Р₂,Р₃ параллельны начальной плоскости Р, а расстояния между ними должны быть одинаковыми; их принято обозначать буквой h и называть высотой сечения рельефа. На топографических картах высота сечения рельефа устанавливается в зависимости от масштаба съемки и от характера местности.

Рис. 2.1. Изображение рельефа горизонталями и высоты сечения рельефа (расстояние по высоте между секущими плоскостями)

    Выбор высоты сечения для изображения неровностей местности горизонталями зависит от масштаба, в котором составляется карта, и от характера рельефа, как было отмечено выше. Следовательно, в гористых местах горизонтали будут при данной высоте сечения гораздо многочисленнее, чем в местах равнинных. Чтобы не затемнять карты излишней густотой горизонталей, высота сечения для горных районов иногда устанавливается большей, а для равнинной местности, чтобы не упустить подробностей и нагляднее выразить неровности, высота сечения, наоборот, уменьшается. По той же причине изменяется высота сечения и на картах разных масштабов: чем мельче масштаб карты, тем больше устанавливают высоту сечения и наоборот. Отметки точек в вершинах квадратов вычисляют в соответствии с формулой

где H – отметка вершины квадрата; h – превышение между репером (H_pn.17) и вершиной квадрата. Вычисленные отметки вершин квадратов выписываются у каждой вершины с округлением до десятых долей. Возьмем сначала точки С и В, имеющие отметки 19,4 м и 25,5 м. Разность отметок точек В и С 25,5 м –19,4 м = 6,1 м.

    Линия СВ при измерении ее масштабной линейкой оказалась равной 50 мм. От точки С по направлению к точке В возвышение равно 6,1 м, при сечении рельефа горизонталями через 1 м между точками С и В пройдут горизонтали с отметками 20, 21, 22, 23, 24, 25 м. От точки С с отметкой 19,4 м до ближайшей к ней 20-й горизонтали превышение равно 20 – 19,4 = 0,6 м. На основании того, что горизонтальное проложение линии ската в направлении от точки С к точке В увеличивается, можно написать пропорцию

где х – расстояние от точки С до 20-й горизонтали. Величина х из этой пропорции определяется как

    Отложив от точки С расстояние, равное 4,9 мм, нанесем положение 20-й горизонтали.

    Рассуждая таким же образом, составим пропорцию для вычисления расстояния до 25-й горизонтали от точки В, т.е.

где х – расстояние по линии ВС от точки В до 25-й горизонтали, а 0,5 есть понижение линии ската от отметки 25,5 до 25,0.