- •1. Задание к курсовой работе
- •2. Построение ряда распределения
- •Исходные статистические данные по урожайности для Нязепетровского района Челябинской области
- •Ранжированный вариационный ряд
- •3. Расчет выборочных параметров ряда распределения
- •Выборочные параметры ряда распределения
- •Построение диаграммы накопленных частот и
- •4.1. Построение диаграммы накопленных частот
- •Данные для построения диаграммы накопленных частот
- •4.2. Построение гистограммы выборки
- •Данные для построения гистограммы выборки
- •5. Проверка основной гипотезы распределения
- •Данные для проверки основной гипотезы
- •6. Линейная диаграмма исходного временного ряда
- •7. Статические показатели временного ряда
- •Аналитические характеристики временного ряда урожайности зерновых
- •Статистические показатели временного ряда
- •8. Сглаживание временного ряда методом скользящей средней
- •Результаты сглаживания временного ряда методом скользящей средней
- •9.Выравнивание временного ряда с помощью линейной функции
- •Результаты выравнивания временного ряда с помощью линейной функции
- •9.Прогнозирование временного ряда на основе линейного тренда
- •Заключение и выводы
- •Библиографический список
5. Проверка основной гипотезы распределения
Если
выборочные асимметрия
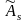 и эксцесс
и эксцесс
 удовлетворяют неравенствам
удовлетворяют неравенствам
 ;
(5.1)
;
(5.1)
и
 ,
(5.2)
,
(5.2)
то изучаемое распределение можно считать нормальным.
Выборочные асимметрия и эксцесс рассчитываются по формулам
 ;
(5.3)
;
(5.3)
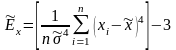 ,
(5.4)
,
(5.4)
где – элементы выборки; – выборочное среднее; – среднеквадратическое отклонение выборки; – объём выборки.
Дисперсия
асимметрии
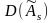 и дисперсия эксцесса
и дисперсия эксцесса
 ,
входящие в выражения (5.1) и (5.2), вычисляются
по формулам
,
входящие в выражения (5.1) и (5.2), вычисляются
по формулам
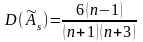 ;
(5.5)
;
(5.5)
 .
(5.6)
.
(5.6)
Итак, проведем расчеты
=
 =
-0,19
=
-0,19
 =
[
=
[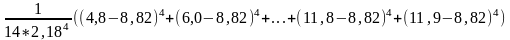 ]
- 3 = 0,86
]
- 3 = 0,86
=
 = 0,3
= 0,3
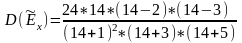 = 0,6
= 0,6
Сведем результаты расчётов в табл. 5.1.
Таблица 5.1
Данные для проверки основной гипотезы
|
|
|
|
Выполнение критерия |
1,13 |
1,64 |
0,86 |
3,9 |
Да |
Таким образом, наша гипотеза о нормальном распределении подтвердилась, т.к. 1,13<1,79 и 0,86<3,84, и данное распределение действительно можно рассматривать как нормальное.
6. Линейная диаграмма исходного временного ряда
Урожайность, наблюдаемую в течение определённого периода времени, можно рассматривать как числовые значения статистического показателя в последовательные моменты времени, т.е. в виде временного ряда или ряда динамики.
Изобразим
на рисунке в
Приложении 3 исходный временной ряд

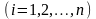 в виде линейной
диаграммы.
в виде линейной
диаграммы.
По оси абсцисс расположим время (годы), а по оси ординат соответствующие этим годам фактические уровни временного ряда . Полученные таким образом точки соединим отрезками прямых линий.
Итак, теперь мы можем графически увидеть зависимость между годом и урожайностью зерна в этот год. На графике видны резкие скачки - различия между значениями урожайности зерна в разные годы.
7. Статические показатели временного ряда
Вычислим основные показатели временного ряда.
1. Абсолютный прирост (цепной и базисный) определяется как разность между двумя уровнями динамического ряда
 ,
(7.1)
,
(7.1)
где
индекс
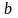 следует заменить
следует заменить
для цепного абсолютного прироста b = i – 1;
для базисного абсолютного прироста b = 1.
Таким образом, если рассчитывается разность между уровнем i-го периода yi и предыдущим уровнем yi-1, то определяем цепной абсолютный прирост. Когда же уровни сопоставляются с исходным показателем ряда y1, то получаем базисный абсолютный прирост.
2. Коэффициент роста (цепной) рассчитывается по формуле
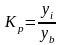 .
(7.2)
.
(7.2)
3. Темп роста (цепной) рассчитывают по формуле
 (%).
(7.3)
(%).
(7.3)
4. Темп прироста (цепной) находят из выражения
 (%).
(7.4)
(%).
(7.4)
5. Абсолютное значение одного процента прироста (цепного или базисного) равно
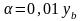 .
(7.5)
.
(7.5)
Абсолютное значение 1 % базисного прироста, в отличие от цепного, является для всего ряда динамики величиной постоянной.
Занесем результаты расчёта в табл. 7.1.
Таблица 7.1