
- •Глава VIII. Ряды.
- •§ 1. Основные понятия.
- •§ 2. Теоремы сравнения.
- •§ 3. Признаки сходимости положительных рядов.
- •Если , то ряд сходится.
- •Если , то ряд расходится.
- •Если , то ряд сходится.
- •Если , то ряд расходится.
- •§ 4. Знакопеременные ряды.
- •§ 5. Функциональные ряды.
- •§ 6. Степенные ряды.
- •§ 7. Ряд Тейлора.
- •§ 7. Ряд Фурье.
- •§ 8. Специальные виды разложения в ряд Фурье.
§ 7. Ряд Тейлора.
Пусть функция
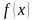 бесконечное число раз дифференцируема
в точке
.
Ряд
бесконечное число раз дифференцируема
в точке
.
Ряд
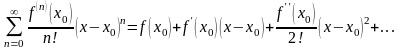
называется рядом Тейлора функции
в точке
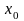 .
Если
.
Если
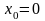 ,
ряд Тейлора называется рядом
Маклорена:
,
ряд Тейлора называется рядом
Маклорена:
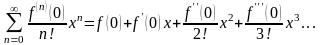
Упражнение
Разложить в ряд Маклорена функцию
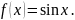
Основные вопросы: сходится ли ряд Тейлора? Какова область сходимости? Сходится равномерно или поточечно? Если ряд сходится равномерно, то к какой функции?
Ряд Тейлора – это частный случай степенного ряда, поэтому всё, что справедливо для степенного ряда, справедливо и для ряда Тейлора.
Теорема 1.
Если производные ограничены:
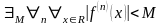 ,
,
то ряд Тейлора сходится равномерно на
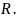
Доказательство.
По условию, ряд
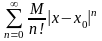 будет являться мажорирующим рядом для
ряда Тейлора. Покажем, что мажорирующий
ряд сходится. По признаку Даламбера:
будет являться мажорирующим рядом для
ряда Тейлора. Покажем, что мажорирующий
ряд сходится. По признаку Даламбера:
 ,
,
поэтому ряд сходится на
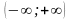 .
Согласно теореме 2 предыдущего параграфа,
ряд Тейлора сходится равномерно на
любом отрезке, содержащемся в
,
т.е. на
.
Согласно теореме 2 предыдущего параграфа,
ряд Тейлора сходится равномерно на
любом отрезке, содержащемся в
,
т.е. на
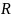 ,
ч.т.д.
,
ч.т.д.
Например, составим ряд Маклорена для
функции
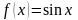 :
:
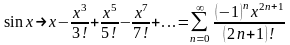 .
.
Все производные, очевидно, ограничены:
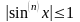 ,
,
поэтому, согласно доказанной теореме, полученный ряд равномерно сходится на .
Заметим, что если производные неограниченны, то это вовсе не означает, что ряд расходится.
Упражнение
Разложить в ряд Маклорена функции
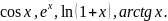
Теорема 2.
Если производные ограничены:
,
то ряд Тейлора сходится к породившей его функции:
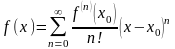 .
.
Доказательство длинное.
Вот как выглядят разложения основных функций в ряд Маклорена (по степеням ):
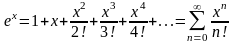 на
.
на
.
В частности,
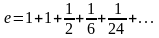 .
.
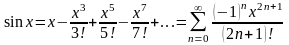 на
.
на
.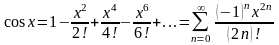 на
.
на
.
Из первых трёх разложений следует, что
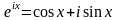 ,
,
поэтому
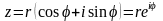 -
-
показательная форма записи комплексного числа.
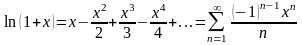 на
на
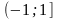 .
.
В частности,
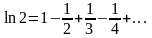 .
.
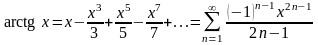 на
на
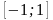 .
.
В частности,
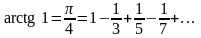 .
.
Упражнение
Используя разложения 1 – 5, разложить в ряд Тейлора функции:
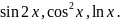
Существует ещё один способ разложения функции в ряд Тейлора: по формуле суммы геометрического ряда:
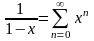 .
.
Упражнение
Разложить в ряд Тейлора функции:
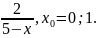
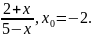
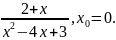
§ 7. Ряд Фурье.
Последовательность функций
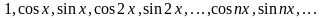
называется тригонометрической последовательностью.
Если две функции
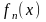 и
и
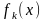 - члены этой последовательности, то
интеграл
- члены этой последовательности, то
интеграл
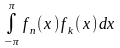
называется скалярным произведением функций и .
Теорема 1.
Тригонометрическая последовательность
ортогональна, т.е. при
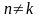
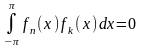 .
.
Для доказательства этой теоремы надо проверить, что справедливы равенства:
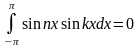 при
;
при
;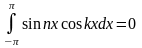 ;
;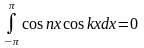 при
;
при
;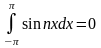 ;
; .
.
Сумма
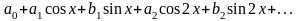
или
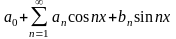 ,
,
где
и
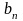 - некоторые числа, называется рядом
Фурье.
- некоторые числа, называется рядом
Фурье.
Разложим произвольную функцию в ряд Фурье, т.е. найдём такие коэффициенты и , чтобы выполнялось равенство
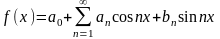 . (*)
. (*)
Проинтегрируем его от – π до π. По теореме 1, все слагаемые в правой части, за исключением одного, обратятся в нуль и получится:
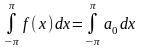 .
.
Отсюда мгновенно следует, что
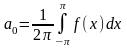 .
.
Если умножить (*) на
 и лишь затем проинтегрировать от – π
до π, то в правой части снова останется
только одно незанулившееся слагаемое.
Получим:
и лишь затем проинтегрировать от – π
до π, то в правой части снова останется
только одно незанулившееся слагаемое.
Получим:
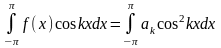 .
.
Вычислив интеграл в правой части, получим
формулу для нахождения
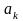 :
:
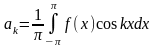 .
.
Аналогичными рассуждениями можно вывести:
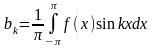 .
.
Заметим, что если
- нечётная функция, то
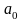 и
равны нулю, поэтому разложение будет
только по синусам. Если же
- чётная функция, то
и
равны нулю, поэтому разложение будет
только по синусам. Если же
- чётная функция, то
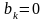 и разложение в ряд Фурье будет только
по косинусам.
и разложение в ряд Фурье будет только
по косинусам.
Упражнение
Разложить в ряд Фурье функции

Обозначим сумму получившего ряда
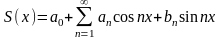 ,
,
где
и
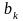 вычислены по предыдущим двум формулам.
Очевидно, функция
вычислены по предыдущим двум формулам.
Очевидно, функция
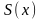 периодическая с периодом
периодическая с периодом
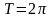 ,
поэтому равенство
,
поэтому равенство
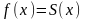 может иметь место на ℝ
только в случае, если
периодическая с периодом
может иметь место на ℝ
только в случае, если
периодическая с периодом
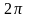 .
Если же
непериодическая или разрывная (точки
разрыва I рода), то надо
продолжить её на ℝ
по принципу периодичности:
.
Если же
непериодическая или разрывная (точки
разрыва I рода), то надо
продолжить её на ℝ
по принципу периодичности:

Тогда для любого из ℝ будет справедливо равенство:

Здесь для краткости обозначены:
 ,
, 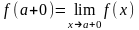 .
.
