Глава VIII. Ряды.
§ 1. Основные понятия.
Числовым рядом называется числовая последовательность, между членами которой поставлен знак «плюс»:
.
Эту сумму можно записать короче, используя знак суммирования:
.
Слагаемое
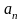называется общим членом ряда.
Сумма первых
членов ряда называется
-й
частичной суммой и обозначается
.
Ряд называется сходящимся, если
сходится последовательность его
частичных сумм
,
т.е. если существует конечное число
,
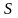такое, что
.
Напомню, по определению сходящейся последовательности, это означает, что
.
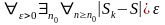Если
не существует или
,
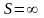то ряд называется расходящимся.
Примеры.
.
.
.
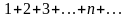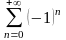Если члены ряда образуют геометрическую прогрессию, то ряд называется геометрическим:
.
Здесь
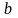- это первый член геометрического ряда,
- его знаменатель. Если
,
геометрическая прогрессия называется
бесконечно убывающей, и у ряда существует
конечная сумма:
,
т.е. при геометрический ряд сходится.
Любой ряд можно представить в виде
.
Первое слагаемое – это -я частичная сумма, а второе слагаемое называется остатком ряда.
Теорема 1.
Ряд и его остаток сходятся или расходятся одновременно.
Доказательство.
Представим ряд в виде
.
Так как частичная сумма
представляет собой сумму
слагаемых, т.е. сумму конечного числа
слагаемых, то
- всегда конечное число. Если остаток
ряда
сходится, то он равен какому-то конечному
числу, но тогда
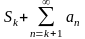тоже конечное число. Следовательно, ряд
также равен конечному числу, поэтому
он сходится.
Обратно аналогично, ч.т.д.
Эту теорему можно переформулировать так: отбрасывание конечного числа членов ряда не влияет на его сходимость.
Теорема 2. (Необходимое условие сходимости ряда)
Если ряд сходится, что его общий член стремится к нулю:
сходится
.
Доказательство.
Очевидно,
.
Если ряд сходится, то, по определению,
сходится его последовательность
частичных сумм. Устремляя в последнем
равенстве
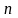к бесконечности, получим:
,
ч.т.д.
Обратное утверждение неверно, т.е. если общий член ряда стремится к нулю, то это не значит, что ряд сходится. Но всегда верна теорема, противоположная обратной, её-то и применяют на практике: если общий член ряда не стремится к нулю, то ряд расходится:
.
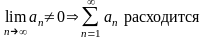Это утверждение называется признаком расходимости ряда.
Примеры.
.
.
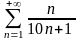§ 2. Теоремы сравнения.
Ряд называется положительным, если все его члены неотрицательны:
.
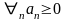В этом случае последовательность
частичных сумм
будет возрастающей, т.е.
.
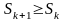У положительного ряда сумма либо конечная
(ряд сходится), либо равна
(ряд расходится). Третьего варианта не
существует.
Теорема сравнения 1.
Если
и
- положительные ряды и
,
то:
;
.
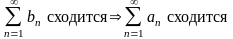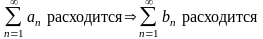Доказательство.
Пусть
,
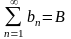а
.
Из условия следует, что
,
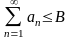поэтому, тем более,
.
Таким образом, последовательность
ограничена сверху. Так как она ещё и
возрастающая, то она имеет предел (глава
I, § 5, св. 8). По определению,
если последовательность частичных
сумм имеет предел, то ряд сходится,
ч.т.д.От противного. Пусть ряд сходится, тогда, по п. а), меньший ряд тоже сходится, что противоречит условию. Это противоречие полностью доказывает теорему. Её можно переформулировать так: из сходимости большего ряда следует сходимость меньшего. Из расходимости меньшего ряда следует расходимость большего.
Примеры.
.
.
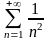Вообще, справедливо утверждение:
Прежде чем перейти ко второй теореме сравнения, заметим, что
.
Теорема сравнения 2.
Если и - положительные ряды и
,
то ряды сходятся или расходятся одновременно.
Доказательство.
По условию,
.
Пусть
,
тогда последнее неравенство примет
вид:
,
.
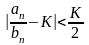Прибавляя ко всем частям двойного
неравенства по
,
получим:
.
Рассмотрим только правую часть этого двойного неравенства. Из неё выведем, что
.
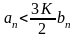Если ряд
сходится, то ряд
тоже сходится (см. замечание перед этой
теоремой). Но тогда, согласно первой
теореме сравнения, меньший ряд
тоже сходится. Половина теоремы доказана.
Рассмотрев левую часть двойного
неравенства, можно доказать и вторую
половину теоремы.
Примеры.
.
.
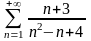Чтобы определить, с каким из рядов
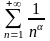сравнивать данный ряд, нужно вычислить
по формуле
.
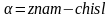