Вычисление поверхностных интегралов I рода.

Если поверхность задана уравнением 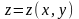, то элемент площади поверхности 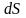вычисляется по формуле, аналогичной той, по которой вычисляется элемент длины дуги (глава III, § 15). Элемент длины дуги вычислялся по формуле

,

а элемент площади поверхности – по формуле

.

Таким образом, поверхностный интеграл I рода можно вычислить так:

,

где - проекция поверхности на плоскость .

Примеры.

1. Вычислить 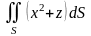, где - верхняя полусфера радиуса 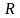с центром в начале координат.

2. Найти площадь части параболоида 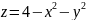, ограниченного плоскостью

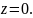
§ 10. Поверхностные интегралы II рода.

Поверхность называется двусторонней, если после обхода по любому замкнутому пути, лежащему на поверхности, направление вектора нормали не меняется:

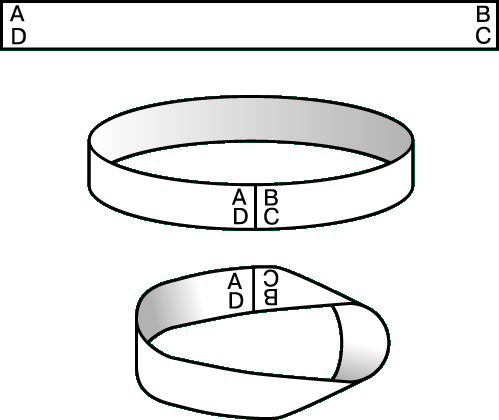
Примером односторонней поверхности может служить лист Мёбиуса:

Пусть - некоторая поверхность, каждой точке которой поставлен в соответствие вектор 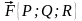, где , 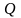и - функции трёх переменных:

, , .

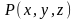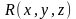Разобьём эту поверхность на частей , на каждой из них выберем произвольную точку :

и в этой точке построим вектор нормали 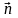, длина которого равна единице. Обозначим площадь 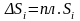. Сумма

называется интегральной суммой. Под записью 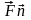здесь понимается скалярное произведение векторов.

Наконец, пусть . Если существует предел

,

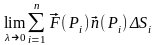который не зависит от разбиения поверхности и от выбора точек , то он называется поверхностным интегралом II рода и обозначается

= .

Если - замкнутая поверхность (ограничивает некоторую пространственную область), то поверхностный интеграл II рода называется потоком вектора через замкнутую поверхность и обозначается

.

Свойства поверхностного интеграла II рода в основном повторяют свойства всех ранее изученных интегралов. Есть лишь одно особенное: поверхностный интеграл II рода зависит от выбора стороны поверхности. При смене стороны поверхности единичный вектор нормали изменит направление на противоположное (сменит знак), скалярное произведение также сменит знак, поэтому и весь интеграл поменяет знак на противоположный.

Если обозначить , 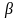, 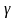углы, которые образует единичный вектор нормали с осями координат 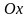, 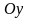и 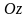соответственно, то вектор будет иметь координаты

.

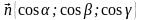Обозначив координаты вектора

,

получим, что их скалярное произведение равно

.

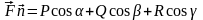Таким образом, поверхностный интеграл II рода можно записать так:

.

Можно показать, что произведение 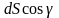представляет собой площадь проекции элемента на плоскость :

.

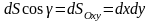Аналогичными рассуждениями получаем, что

; .

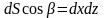Поэтому иногда поверхностный интеграл II рода записывается так:

.

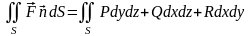Эта запись объясняет, почему поверхностный интеграл II рода называют, по аналогии с криволинейным интегралом II рода, интегралом по координатам. Однако вычисление поверхностного интеграла II рода удобнее всего производить непосредственно по определению, по формуле

.

Координаты вектора обычно заданы, координаты вектора нормали к поверхности , заданной неявно, мы находить умеем (гл. IV, § 8):

,

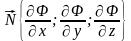а чтобы сделать вектор 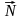единичным (пронормировать), нужно просто разделить каждую его координату на его длину:

.

После этого поверхностный интеграл II рода сведётся к поверхностному интегралу I рода:

,

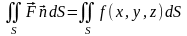а его мы уже вычислять умеем.

Пример.

Вычислить

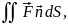
где S – часть плоскости 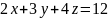, расположенная в I октанте, а 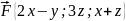. Ответ 79.

Если поверхностный интеграл II рода вычисляется по замкнутой поверхности, то справедлива формула Остроградского-Гаусса:

,

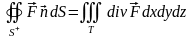где - пространственное тело, которое ограничивается замкнутой поверхностью , а дивергенция вектора вычисляется по формуле

.

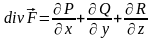При этом значком 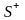обозначают внешнюю сторону замкнутой поверхности . Т.е. формула Остроградского-Гаусса справедлива только в случае, если вектор нормали направлен наружу.

Пример.

Вычислить

по части плоскости , расположенной в I октанте.