
- •Глава VI. Дифференциальные уравнения.
- •§ 1. Основные понятия.
- •§ 2. Уравнения первого порядка.
- •§ 3. Понижение порядка дифференциального уравнения.
- •§ 4. Линейно независимые функции.
- •§ 5. Линейные уравнения.
- •§ 6. Решение линейных однородных уравнений 2-го порядка с постоянными коэффициентами,
- •§ 7. Решение линейных неоднородных уравнений 2-го порядка с постоянными коэффициентами,
- •Метод вариации постоянных.
- •§ 8. Системы линейных дифференциальных уравнений первого порядка,
- •Глава VII. Кратные, криволинейные и поверхностные интегралы.
- •§ 1. Интеграл по прямоугольнику.
- •Свойства интеграла.
- •Геометрический смысл двойного интеграла.
- •§ 2. Интеграл по междуграфику.
- •§ 3. Переход к полярным координатам.
- •§ 4. Тройной интеграл.
- •§ 5. Переход к сферическим координатам.
- •§ 6. Криволинейные интегралы I рода.
- •Геометрический смысл.
- •Вычисление криволинейного интеграла I рода.
- •§ 7. Криволинейные интегралы II рода.
- •Свойства.
- •Физический смысл.
- •Вычисление криволинейного интеграла II рода.
- •Связь между криволинейными интегралами I и II родов.
- •§ 8. Формула Грина.
- •§ 9. Условие независимости криволинейного интеграла II рода от пути.
- •§ 10. Поверхностные интегралы I рода.
- •Вычисление поверхностных интегралов I рода.
- •§ 10. Поверхностные интегралы II рода.
- •§ 11. Формула Стокса.
- •§ 12. Элементы векторного анализа
§ 9. Условие независимости криволинейного интеграла II рода от пути.
Рассмотрим интеграл
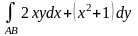 и вычислим его по отрезку, соединяющему
точки
и вычислим его по отрезку, соединяющему
точки
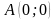 и
и
 .
Затем вычислим этот же самый интеграл
по дуге параболы, соединяющей точки
и
.
Увидим, что ответы получились одинаковыми.
И это не случайно. Иногда значение
интеграла зависит только от начальной
и конечной точки и не зависит от пути
интегрирования. В этом случае интеграл
можно вычислить по формуле, напоминающей
формулу Ньютона-Лейбница:
.
Затем вычислим этот же самый интеграл
по дуге параболы, соединяющей точки
и
.
Увидим, что ответы получились одинаковыми.
И это не случайно. Иногда значение
интеграла зависит только от начальной
и конечной точки и не зависит от пути
интегрирования. В этом случае интеграл
можно вычислить по формуле, напоминающей
формулу Ньютона-Лейбница:
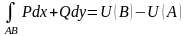 .
.
Первый вопрос: что понимать под первообразной ? Очевидно, это функция, дифференциал которой равен подынтегральному выражению:
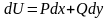 .
.
Второй вопрос: как найти эту первообразную? Естественно, интегрированием. Для примера вычислим интеграл
от
точки
до точки
.
У нас
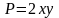 ,
,
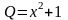 .
.
Находим первообразную , точнее говоря, её первую часть:
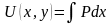
 .
.
Функция
 выступает в роли константы, ибо при
интегрировании по переменной
мы считаем
постоянным.
выступает в роли константы, ибо при
интегрировании по переменной
мы считаем
постоянным.
Находим функцию . Каким образом? Формула вычисления дифференциала функции двух переменных такова:
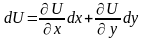 .
.
С другой стороны, у нас . Сопоставляя эти формулы, увидим, что
.
Отсюда уравнение:
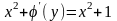 .
.
Решая его, находим функцию :
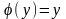 .
.
Как и в формуле Ньютона-Лейбница, достаточно найти только одну из первообразных. Тем самым мы выяснили, что
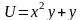 .
.
Получилось:
 .
.
Третий вопрос: в каком случае криволинейный интеграл II рода можно вычислять по формуле
?
Ответ:
если существует функция
 ,
такая, что
,
такая, что
.
Дело в том, что первообразная существует далеко не всегда.
Наконец, последний вопрос: как определить, существует первообразная или нет? Ответ такой же, как и на вопрос о том, будет ли данное дифференциальное уравнение уравнением в полных дифференциалах? Если
,
то первообразная существует.
Замечание 1.
В ходе наших рассуждений выяснилось, что следующие утверждения эквивалентны:
Интеграл
 не зависит от пути интегрирования.
не зависит от пути интегрирования.По любому замкнутому пути
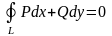 .
.Выполняется тождество .
Существует функция , такая, что .
Замечание 2.
Работа силы тяжести не зависит от траектории движения тела, над которым совершается работа, а зависит только от начальной и конечной точек. При этом она равна разности потенциальных энергий тела в точках и :
 .
.
§ 10. Поверхностные интегралы I рода.
Диаметром множества
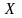 называется наибольшее расстояние между
любыми его двумя точками:
называется наибольшее расстояние между
любыми его двумя точками:
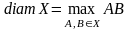 .
.
Пусть задана функция
 и поверхность
и поверхность
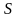 ,
содержащаяся в области определения
этой функции. Разобьём эту поверхность
на
частей
,
содержащаяся в области определения
этой функции. Разобьём эту поверхность
на
частей
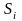 и обозначим
и обозначим
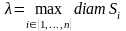 .
.

На каждой из частичек
выберем произвольную точку
 и составим сумму
и составим сумму
 ,
,
где
значком
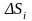 обозначена площадь частички
.
обозначена площадь частички
.
Если существует предел
 ,
,
который не зависит разбиения поверхности и выбора точек , то он называется поверхностным интегралом I рода и обозначается
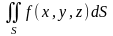 .
.
Его свойства практически совпадают со свойствами криволинейного интеграла I рода:
 .
.
 .
. ,
если поверхность
состоит из поверхностей
,
если поверхность
состоит из поверхностей
 и
и
 ,
не пересекающихся внутренним образом.
,
не пересекающихся внутренним образом. - площадь поверхности
.
- площадь поверхности
.
В самом деле, если
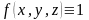 ,
то интегральная сумма
,
то интегральная сумма
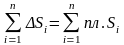 ,
,
естественно, равна площади поверхности .
Если функция
 ,
то её можно ассоциировать с поверхностной
плотностью, поэтому
,
то её можно ассоциировать с поверхностной
плотностью, поэтому
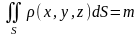 ,
,
где - масса поверхности .
