
- •Глава VI. Дифференциальные уравнения.
- •§ 1. Основные понятия.
- •§ 2. Уравнения первого порядка.
- •§ 3. Понижение порядка дифференциального уравнения.
- •§ 4. Линейно независимые функции.
- •§ 5. Линейные уравнения.
- •§ 6. Решение линейных однородных уравнений 2-го порядка с постоянными коэффициентами,
- •§ 7. Решение линейных неоднородных уравнений 2-го порядка с постоянными коэффициентами,
- •Метод вариации постоянных.
- •§ 8. Системы линейных дифференциальных уравнений первого порядка,
- •Глава VII. Кратные, криволинейные и поверхностные интегралы.
- •§ 1. Интеграл по прямоугольнику.
- •Свойства интеграла.
- •Геометрический смысл двойного интеграла.
- •§ 2. Интеграл по междуграфику.
- •§ 3. Переход к полярным координатам.
- •§ 4. Тройной интеграл.
- •§ 5. Переход к сферическим координатам.
- •§ 6. Криволинейные интегралы I рода.
- •Геометрический смысл.
- •Вычисление криволинейного интеграла I рода.
- •§ 7. Криволинейные интегралы II рода.
- •Свойства.
- •Физический смысл.
- •Вычисление криволинейного интеграла II рода.
- •Связь между криволинейными интегралами I и II родов.
- •§ 8. Формула Грина.
- •§ 9. Условие независимости криволинейного интеграла II рода от пути.
- •§ 10. Поверхностные интегралы I рода.
- •Вычисление поверхностных интегралов I рода.
- •§ 10. Поверхностные интегралы II рода.
- •§ 11. Формула Стокса.
- •§ 12. Элементы векторного анализа
Вычисление криволинейного интеграла I рода.
Если дуга задана параметрическим уравнением:

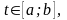
то, как мы знаем, (глава III, §15) элемент длины дуги вычисляется по формуле
 .
.
Отсюда
 .
.
При
этом надо обязательно следить, чтобы
было
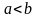 .
.
§ 7. Криволинейные интегралы II рода.
Пусть некоторое тело движется по дуге
 ,
расположенной в плоскости
под действием силы
,
расположенной в плоскости
под действием силы
 .
В общем случае сила меняется от точки
к точке, поэтому каждая координата
вектора силы является функцией двух
переменных:
.
В общем случае сила меняется от точки
к точке, поэтому каждая координата
вектора силы является функцией двух
переменных:
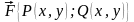 .
.
Задача
состоит в том, чтобы найти работу силы
по перемещения тела из точки
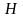 в точку
.
в точку
.

По традиции разобьём дугу на частей и длину наибольшей дуги разбиения обозначим :
,
где
- длина дуги
.
Работу силы на каждой из дуг
обозначим
 .
При
.
При
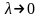 перемещение тела по дуге
можно считать перемещением по вектору
перемещение тела по дуге
можно считать перемещением по вектору
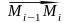 ,
а силу
можно считать постоянной и вычислять
в произвольной точке
,
а силу
можно считать постоянной и вычислять
в произвольной точке
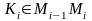 .
Для прямолинейного движения под действием
постоянной силы остаётся справедливой
школьная формула вычисления работы:
.
Для прямолинейного движения под действием
постоянной силы остаётся справедливой
школьная формула вычисления работы:
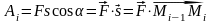 .
.
Для
нахождения скалярного произведения
векторов
 и
и
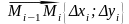 используем опять же школьную формулу
используем опять же школьную формулу
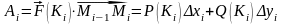 .
.
Чтобы найти работу на всей дуге , нужно, естественно, просуммировать:

 .
.
Получившееся выражение называется интегральной суммой криволинейного интеграла II рода.
Если существует предел
 ,
,
который не зависит от разбиения дуги и выбора точек Кi, то он называется интегралом по координатам или криволинейным интегралом II рода от функции . Обозначение такое:
 .
.
Свойства.
Повторяться не будем, перечислим только основные:
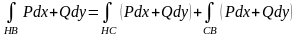 ,
если точка
принадлежит дуге
.
,
если точка
принадлежит дуге
. ,
т.е. значение криволинейного интеграла
II рода зависит от
направления интегрирования. Это
связано с тем, что если при движении по
кривой от точки
к точке
приращения
,
т.е. значение криволинейного интеграла
II рода зависит от
направления интегрирования. Это
связано с тем, что если при движении по
кривой от точки
к точке
приращения
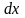 и
и
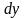 были, например, положительными, то при
движении в обратном направлении они
станут отрицательными.
были, например, положительными, то при
движении в обратном направлении они
станут отрицательными.Физический смысл.
 ,
,
где
- работа силы
 по перемещению тела их точки
в точку
.
по перемещению тела их точки
в точку
.
Вычисление криволинейного интеграла II рода.
Если дуга задана параметрическим уравнением:
где
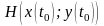 ,
,
 ,
то вполне естественно, что
,
то вполне естественно, что
 .
.
При
этом надо обязательно следить, чтобы
точке
соответствовало значение
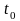 ,
а точке
- значение
,
а точке
- значение
 .
.
В частности, если кривая задана явным
уравнением
 ,
то
,
то
 .
.
Связь между криволинейными интегралами I и II родов.
Обозначим углы, которые образует вектор
 с осями координат:
с осями координат:
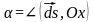 ,
, 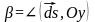 .
.

Очевидно,
 ,
,  ,
,
где
 .
Поэтому
.
Поэтому
 .
.
§ 8. Формула Грина.
Она связывает интеграл по замкнутой
кривой
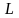 и двойной интеграл по области
,
ограниченной этой замкнутой кривой.
и двойной интеграл по области
,
ограниченной этой замкнутой кривой.
Если начало и конец дуги совпадают, то она называется замкнутой. Криволинейный интеграл II рода по замкнутой кривой называется интегралом по замкнутому пути или циркуляцией вектора по замкнутому контуру . Обозначение такое:
 .
.
Если замкнутый путь пробегается против хода часовой стрелки (направление обхода положительное), то справедлива формула Грина:
 .
.
Доказательство.
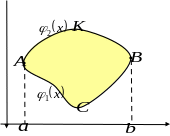
 .
.
Вычислим отдельно последний интеграл:
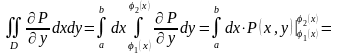


В предыдущем параграфе мы могли видеть, что
,
откуда, в частности, следует, что
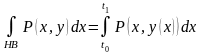 .
.
Применяя последнюю формулу, получим:

 .
.
Итак, доказано, что
 .
Аналогичными рассуждениями можно
показать, что
.
Аналогичными рассуждениями можно
показать, что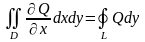 .
Вычитая из последнего равенства
предпоследнее, мы и получим формулу
Грина.
.
Вычитая из последнего равенства
предпоследнее, мы и получим формулу
Грина.
Обычно формула Грина применяется слева направо:
,
т.е. с помощью двойного интеграла мы вычисляем криволинейный интеграл II рода. Но можно использовать формулу Грина и в обратном направлении. В частности:
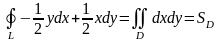 .
.
Поэтому криволинейный интеграл II рода по замкнутому пути можно использовать для вычисления площади плоской фигуры, ограниченной этим замкнутым путём:
 .
.
