
- •Глава VI. Дифференциальные уравнения.
- •§ 1. Основные понятия.
- •§ 2. Уравнения первого порядка.
- •§ 3. Понижение порядка дифференциального уравнения.
- •§ 4. Линейно независимые функции.
- •§ 5. Линейные уравнения.
- •§ 6. Решение линейных однородных уравнений 2-го порядка с постоянными коэффициентами,
- •§ 7. Решение линейных неоднородных уравнений 2-го порядка с постоянными коэффициентами,
- •Метод вариации постоянных.
- •§ 8. Системы линейных дифференциальных уравнений первого порядка,
- •Глава VII. Кратные, криволинейные и поверхностные интегралы.
- •§ 1. Интеграл по прямоугольнику.
- •Свойства интеграла.
- •Геометрический смысл двойного интеграла.
- •§ 2. Интеграл по междуграфику.
- •§ 3. Переход к полярным координатам.
- •§ 4. Тройной интеграл.
- •§ 5. Переход к сферическим координатам.
- •§ 6. Криволинейные интегралы I рода.
- •Геометрический смысл.
- •Вычисление криволинейного интеграла I рода.
- •§ 7. Криволинейные интегралы II рода.
- •Свойства.
- •Физический смысл.
- •Вычисление криволинейного интеграла II рода.
- •Связь между криволинейными интегралами I и II родов.
- •§ 8. Формула Грина.
- •§ 9. Условие независимости криволинейного интеграла II рода от пути.
- •§ 10. Поверхностные интегралы I рода.
- •Вычисление поверхностных интегралов I рода.
- •§ 10. Поверхностные интегралы II рода.
- •§ 11. Формула Стокса.
- •§ 12. Элементы векторного анализа
§ 3. Переход к полярным координатам.
В случаях если область интегрирования ограничена окружностями или прямыми, проходящими через начало координат, бывает полезно перейти к полярным координатам. Напомню формулы перехода:
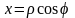 ,
,
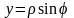 .
.
Верна ли формула
 ?
?
Изобразим геометрически элемент
интегрирования
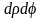 .
Это площадь прямоугольничка
.
Это площадь прямоугольничка
 :
:
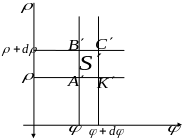
Теперь найдём прообраз этого прямоугольничка, т.е. фигуру, из которой он получился при преобразованиях координат , :
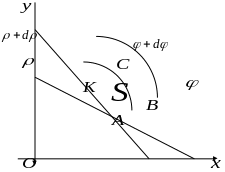
Площадь
криволинейного прямоугольничка
 можно вычислить как разность площадей
секторов:
можно вычислить как разность площадей
секторов:
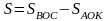 .
.
Напомню,
что площадь сектора находится по
формуле ,
где
,
где
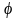 - это центральный угол. В нашем случае
он равен
- это центральный угол. В нашем случае
он равен
 .
Получаем:
.
Получаем:
 .
.
При
малых значениях
 вторым слагаемым можно пренебречь,
поэтому считаем, что
вторым слагаемым можно пренебречь,
поэтому считаем, что
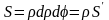 .
.
Делаем вывод:

Таким образом, справедлива формула:
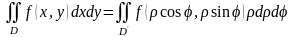 .
.
Это частный случай общей формулы
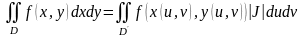 ,
,
где
 - якобиан:
- якобиан:
 .
.
Проверь,
что в нашем случае якобиан был равен
 .
.
§ 4. Тройной интеграл.
Он определяется точно таким же образом, как и двойной. Перечислим основные свойства тройного интеграла:
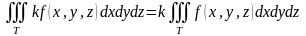 .
. .
.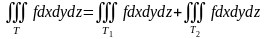 (если
(если
 и
и
 не имеет общих внутренних точек с
не имеет общих внутренних точек с
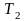 ).
).–
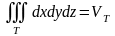 .
.Если
 - прямоугольный параллелепипед:
- прямоугольный параллелепипед:
 ,
,
то
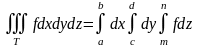 .
.
Пусть - проекция тела на плоскость
 .
Если
- междуграфик, т.е. фигура,
ограниченная снизу и сверху поверхностями
.
Если
- междуграфик, т.е. фигура,
ограниченная снизу и сверху поверхностями
 и
и
 ,
а с боков – боковой поверхностью
цилиндра с основанием
:
,
а с боков – боковой поверхностью
цилиндра с основанием
:
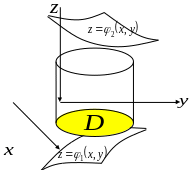
то
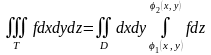 .
.
Замечание.
Иногда удобно рассмотреть проекцию
тела
не на плоскость
,
а на другую координатную плоскость.
Например, если
- проекция тела
на плоскость
 ,
то
,
то
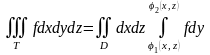 ,
,
где
 и
и
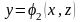 - поверхности, которые ограничивают
тело
слева и справа соответственно.
- поверхности, которые ограничивают
тело
слева и справа соответственно.
§ 5. Переход к сферическим координатам.
Сферические координаты похожи на географические или астрономические, только для задания точки в пространстве нужны три координаты, а для определения точки на поверхности Земли достаточно двух: широты и долготы.
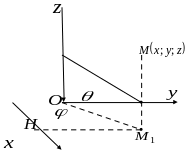
Очевидно,

Отсюда формулы перехода от декартовых координат к сферическим:


Чтобы в тройном интеграле перейти к сферическим координатам, надо вычислить якобиан. Теперь это уже определитель третьего порядка:

поэтому
 .
.
§ 6. Криволинейные интегралы I рода.
Пусть
- некоторая функция, определённая в
точках дуги
 ,
расположенной в плоскости
.
Разобьём дугу
на
частей:
,
расположенной в плоскости
.
Разобьём дугу
на
частей:
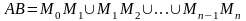 .
.
Обозначим
 длину дуги
длину дуги
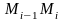 :
:
 .
.
Длину наибольшей дуги разбиения обозначим, как обычно:
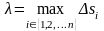 .
.

На
каждой из дуг разбиения выберем
произвольную точку
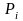 :
:
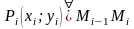 .
.
Сумма

называется интегральной суммой. Если существует предел
 ,
,
который не зависит от разбиения дуги и выбора точек , то он называется интегралом по дуге функции или криволинейным интегралом I рода. Обозначение такое:
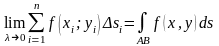 .
.
Величина
 - это элемент длины дуги. У криволинейного
интеграла I рода имеются
свойства, которые в основном повторяют
свойства уже известных нам интегралов:
- это элемент длины дуги. У криволинейного
интеграла I рода имеются
свойства, которые в основном повторяют
свойства уже известных нам интегралов:
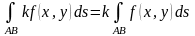 .
. .
. ,
если точка
принадлежит дуге
.
,
если точка
принадлежит дуге
.Геометрический смысл.
Если , то
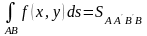 ,
,
где
 - цилиндрическая поверхность с
вертикальными образующими, ограниченная
снизу дугой
,
а сверху – поверхностью
:
- цилиндрическая поверхность с
вертикальными образующими, ограниченная
снизу дугой
,
а сверху – поверхностью
:

Справедливость этого свойства следует
из того, что каждое слагаемое интегральной
суммы
можно рассматривать как произведение
длины средней линии
 трапеции с высотой
.
А это ни что иное, как площадь маленькой
трапеции. Суммируя все площади маленьких
трапеций, мы и получим
трапеции с высотой
.
А это ни что иное, как площадь маленькой
трапеции. Суммируя все площади маленьких
трапеций, мы и получим
 ,
ч.т.д.
,
ч.т.д.
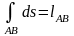 - длина дуги
.
- длина дуги
.
В самом деле, если
 ,
то интегральная сумма
,
то интегральная сумма
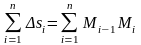 ,
,
естественно, равна длине дуги .
Если функция , то её можно ассоциировать с плотностью кривой , поэтому
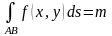 ,
,
где - масса дуги .
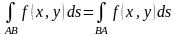 ,
т.е. значение криволинейного интеграла
I рода не
зависит от направления интегрирования.
Это связано с тем, что элементом
интегрирования является элемент длины
дуги
,
который, естественно, всегда положителен,
независимо от того, в какую сторону
двигаться.
,
т.е. значение криволинейного интеграла
I рода не
зависит от направления интегрирования.
Это связано с тем, что элементом
интегрирования является элемент длины
дуги
,
который, естественно, всегда положителен,
независимо от того, в какую сторону
двигаться.
