Глава VII. Кратные, криволинейные и поверхностные интегралы.

§ 1. Интеграл по прямоугольнику.

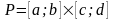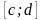Пусть функция определена в прямоугольнике . Разобьём отрезок на частей, а отрезок - на 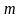частей:

;

.

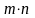Прямоугольник разобьётся на прямоугольничков 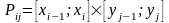. В каждом из прямоугольничков разбиения возьмём произвольную точку: :

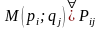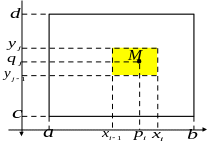
Обозначим 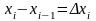, а 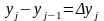. Выражение называется интегральной суммой. Обозначим буквой наибольшую длину диагонали прямоугольничков разбиения и устремим к нулю.

Если существует предел интегральной суммы, который не зависит от разбиения прямоугольника и выбора точек 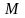, то функция называется интегрируемой по Риману на прямоугольнике , а этот предел называется интегралом по прямоугольнику и обозначается так:

.

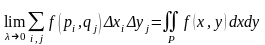Свойства интеграла.

1. Постоянный множитель можно выносить за знак интеграла:

.

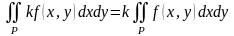2. Интеграл от суммы (разности) двух функций равен сумме (разности) интегралов:

.

3. Если и прямоугольники и 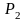не имеют общих внутренних точек:

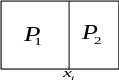
то

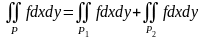
Справедливость первых двух свойств следует из свойств пределов функций (§ 6, глава I), а третье свойство становится очевидным, если при разбиении отрезка одну из точек взять на границе прямоугольников (см. рисунок).

4. Геометрический смысл двойного интеграла.

Если , то

,

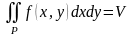где 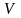- объём параллелепипеда, верхняя грань которого представляет собой часть поверхности , расположенной над прямоугольником :

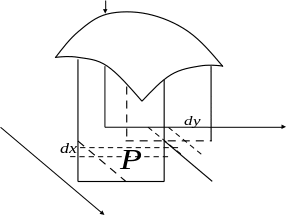
Это свойство можно пояснить так: произведение есть ни что иное, как площадь прямоугольничка разбиения, т.е. площадь основания; - это высота параллелепипедика. Таким образом, умножая площадь основания на высоту, мы получаем объём параллелепипедика, расположенного над прямоугольничком с площадью и ограниченного сверху поверхностью. Знак двойного интеграла предполагает суммирование объёмов всех таких параллелепипедиков. Но сложение всех объёмов, естественно, приведёт нас к объёму большого параллелепипеда, что и утверждается этим свойством.

5. С помощью двойного интеграла можно вычислить площадь прямоугольника:

.

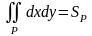Это свойство является прямым следствием предыдущего свойства.

Замечание.

Все рассмотренные свойства двойного интеграла остаются справедливыми и в том случае, когда интегрирование ведётся не по прямоугольнику, а по произвольной области . Но об этом чуть позже. Сначала

теорема о повторном интегрировании.

Если непрерывна на прямоугольнике 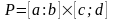, то она интегрируема и

.

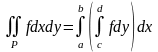Доказательство.

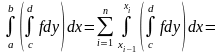
применяем теорему о среднем (глава III, § 10):

поэтому

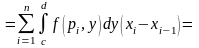
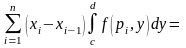
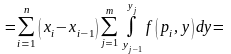
снова применяем теорему о среднем:

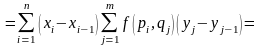
устремляя длину наибольшей диагонали прямоугольничков разбиения к нулю, получим окончательно:

, ч.т.д.

Замечание.

Вместо записи

пишут так:

.

§ 2. Интеграл по междуграфику.

Рассмотрим междуграфик , ограниченный слева и справа прямыми 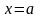и , а снизу и сверху – графиками функций и :

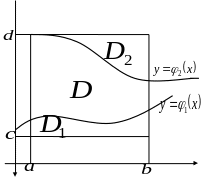
Рассмотрим также прямоугольник , содержащий междуграфик . Определим функцию 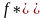таким образом:

Вычислим 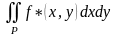двумя способами и приравняем результаты:

1. =

по свойству 3 предыдущего параграфа,

см. определение функции

.

2. 

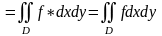см. теорему о повторном интегрировании

см. определение функции

.

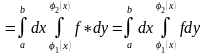Таким образом, получили:

.

Аналогично, если междуграфик ограничен снизу и сверху прямыми и , а слева и справа – графиками функций и :

то

.
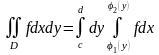