§ 7. Решение линейных неоднородных уравнений 2-го порядка с постоянными коэффициентами,

т.е. уравнений вида , где .

На первый взгляд, здесь всё просто:

1. Отбросить правую часть и найти общее решение однородного уравнения 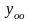(см. предыдущий параграф).

2. Найти какое-нибудь частное решение неоднородного уравнения .

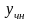3. Записать ответ: (см. § 5, теорема 3).

Так что нам осталось только научиться находить частное решение неоднородного уравнения. Здесь возможны варианты.

1. Если правая часть уравнения представляет собой произведение многочлена -й степени на показательную функцию:

,

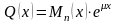и при этом

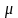1. не является корнем характеристического уравнения, т.е.

,

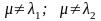то частное решение уравнения следует искать в этом же виде, т.е. в виде произведения многочлена -й степени на .

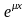Например, если , то частное решение надо искать в виде

.

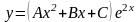2. совпадает с одним из корней характеристического уравнения, т.е.

,

то частное решение уравнения следует искать в виде

.

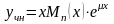Например, если 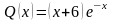, то частное решение будет таким:

.

3. ,

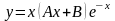то частное решение уравнения ищем в виде

.

Например, если , то частное решение запишется так:

.

2. Если правая часть уравнения имеет вид

,

то надо считать, что 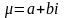. Теперь снова если

1. не является корнем характеристического уравнения, т.е.

,

то частное решение следует искать в виде

,

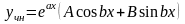где 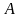и 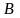- некоторые числа.

Например, если , то частное решение примет такой вид:

.

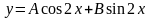Если , то частное решение будет таким:

.

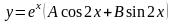2. является одним из корней характеристического многочлена, т.е.

,

то частное решение надо искать в виде

.

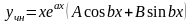Например, если 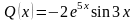, то частное решение будет таким:

.

3. Если правая часть уравнения имеет общий вид, то нужно использовать уже частично знакомый нам метод вариации постоянных.

Метод вариации постоянных.

Итак, ситуация такова: нужно решить линейное неоднородное уравнение

,

правая часть которого не является специальной, т.е. не подходит под пункты 1 и 2. Для этого сначала отбрасываем правую часть и находим общее решение линейного однородного уравнения:

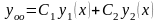
(см. предыдущий параграф). Далее считаем, что и - функции от , и пытаемся изменять (варьировать) их таким образом, чтобы функция

стала решением исходного неоднородного уравнения.

Справедливо утверждение: если функции и являются решением системы

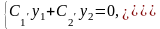
то функция является общим решением исходного уравнения.

Доказательство.

Найдём первые две производные последней функции:

;

.

Подставим эти производные и саму функцию в исходное уравнение и убедимся, что получится тождество:

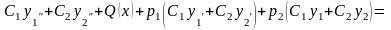
, ч.т.д.

§ 8. Системы линейных дифференциальных уравнений первого порядка,

т.е. системы вида

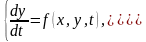
где функции и 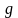линейны по всем трём аргументам ( , и 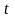входят либо в первой, либо в нулевой степени). Например,

является системой линейных дифференциальных уравнений первого порядка, а среди систем

уже не все являются системами линейных дифференциальных уравнений первого порядка.

Решением системы дифференциальных уравнений является уже не функция, а пара функци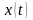й и 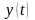, которая обращает каждое из уравнений системы в тождество.

Чтобы решить систему дифференциальных уравнений, нужно:

1. Произвольное уравнение (например, первое) продифференцировать по переменной . При этом в правой части обязательно появится производная .

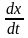2. Подставить вместо функции её выражение из второго уравнения.

3. Выразить из первого уравнения системы переменную через , и и тоже подставить в продифференцированное уравнение.

4. Решить получившееся дифференциальное уравнение второго порядка относительно функции .

5. Используя выражение для из п.3, найти функцию .