Среднестатистический студент не в состоянии выполнять трудноалгоритмизируемые виды деятельности.

В. А. Лукьянов

Глава VI. Дифференциальные уравнения.

§ 1. Основные понятия.

Дифференциальным уравнением называется равенство вида

.

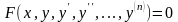При этом число 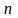(наивысший порядок производной) называется порядком дифференциального уравнения. Например, 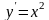- дифференциальное уравнение 1-го порядка, а 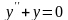- дифференциальное уравнение 2-го порядка.

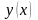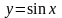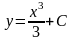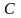Решением дифференциального уравнения называется функция , обращающая его в верное равенство. Например, функция является решением уравнения , а функция является решением уравнения . Нетрудно заметить, что любая функция вида , где - произвольное число, также является решением уравнения . Это решение зависит уже не только от , но и от , т.е. имеет вид 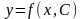. 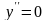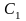Все решения дифференциального уравнения записываются в виде , где и 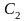произвольные постоянные. В этом случае решение зависит от двух произвольных постоянных, т.е. имеет вид 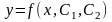. И вообще, решение уравнения -го порядка зависит от произвольных постоянных и может быть записано так:

.

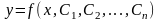Решение дифференциального уравнения, зависящее от произвольных постоянных называется его общим решением. Т.е. - это общее решение уравнения ; - общее решение уравнения .

Если в общем решении дифференциального уравнения произвольным постоянным 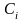придать какие-то конкретные значения, мы получим частное решение дифференциального уравнения. Например, 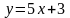является частным решением уравнения . Функция является частным решением уравнения .

Иногда требуется найти не общее решение дифференциального уравнения, а именно частное решение, удовлетворяющее определённым требованиям, которые называются начальными условиями. Например, найти решение уравнения при условии, что 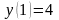. Это условие помогает найти постоянную из общего решения .

Задача Коши – найти частное решение д.у при заданных начальных условиях.

Упражнение.

Записать 2-й закон Ньютона

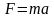
в виде дифференциального уравнения.

§ 2. Уравнения первого порядка.

Если в дифференциальном уравнении 1-го порядка 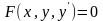выражена производная 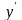, т.е. оно записано так:

,

мы будем говорить, что оно записано в нормальном виде.

1. Если в этом уравнении функция 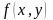такова, что её можно представить в виде произведения функции только от на функцию только от 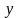, т.е.

,

то оно называется уравнением с разделяющимися переменными. Например, уравнение является уравнением с разделяющимися переменными, а среди уравнений

,

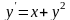уже не все являются уравнениями с разделяющимися переменными.

Уравнения с разделяющимися переменными решаются так:

,

,

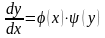после чего переменная окажется только в левой части, а переменная - только в правой (переменные разделятся, отсюда и название уравнения). Интегрируя левую и правую части последнего уравнения, можно найти общее решение дифференциального уравнения.

Упражнение.

Решить задачу о распаде радия. Первоначальная масса куска радия 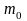. Известно, что скорость уменьшения массы радия прямо пропорциональна его массе. Найти массу радия в произвольный момент времени, т.е. найти функцию .

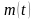2. Если в уравнении функция такова, что

,

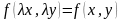где 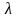произвольное число, то оно называется однородным. Например, уравнение 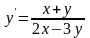является однородным, а среди уравнений

,

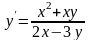уже не все являются однородными.

Для решения однородного уравнения нужно сделать замену , 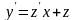. После этого всегда получается уравнение с разделяющимися переменными.

3. Если уравнение может быть записано в виде

,

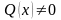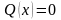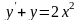то оно называется линейным дифференциальным уравнением 1-го порядка. При этом если , то оно называется линейным неоднородным, если же , оно называется линейным однородным. Но при этом не надо путать его с просто однородным уравнением, задаваемым формулой при условии, что ! Например, уравнение является линейным неоднородным, а среди уравнений

,

,

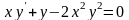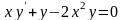
уже не все являются линейными.

Для решения линейного неоднородного уравнения нужно сначала отбросить его правую часть и решить линейное однородное 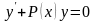. Оно является уравнением с разделяющимися переменными. Далее применять метод вариации постоянной.

4. Если уравнение может быть записано в виде

,

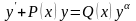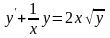где - любое действительное число, то оно называется уравнением Бернулли. Заметь, что при уравнение Бернулли становится линейным уравнением. Например, уравнение является уравнением Бернулли. А среди уравнений

,

,

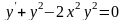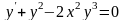
уже не все являются уравнениями Бернулли.

5. Если записать уравнение в виде

,

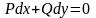и при этом будет выполняться условие

,

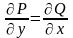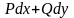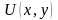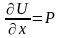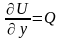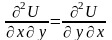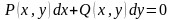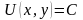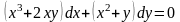то оно называется уравнением в полных дифференциалах. В этом случае является дифференциалом некоторой функции , причём , а . Требование означает равенство смешанных производных: . Уравнение можно переписать так: , следовательно, функция должна быть постоянной. Поэтому общее решение уравнения в полных дифференциалах записывается в виде . Например, уравнение является уравнением в полных дифференциалах, а среди уравнений

,

,

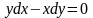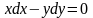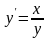
уже не все являются уравнениями в полных дифференциалах.