Билет № 13.

1)Электромагнитные колебания в контуре.

Электромагнитные колебания - это периодические изменения заряда, силы тока и напря-

жения, происходящие в электрической цепи. Простейшей системой для наблюдения электро-

магнитных колебаний служит колебательный контур.

Колебательный контур - это замкнутый контур, образованный последовательно соединённы-

ми конденсатором и катушкой.

Зарядим конденсатор, подключим к нему катушку и замкнём цепь. Начнут происходить

Свободные электромагнитные колебания - периодические изменения заряда на конденсаторе

и тока в катушке. Свободными, напомним, эти колебания называются потому, что они совер-

шаются без какого-либо внешнего воздействия только за счёт энергии, запасённой в контуре.

2)Спектральные серии(линейный спектр атома водорода).

Спектральные серии водорода — набор спектральных серий, составляющих спектр атома водорода. Поскольку водород — наиболее простой атом, его спектральные серии наиболее изучены. Они хорошо подчиняются формуле Ридберга:

,

где R = 109 677 см−1 — постоянная Ридберга для водорода,  — основной уровень серии. Спектральные линии возникающие при переходах на основной энергетический уровень называются резонансными, все остальные — субординатными.

Серия Лаймана - Открыта Т. Лайманом в 1906 году. Все линии серии находятся в ультрафиолетовом диапазоне. Серия соответствует формуле Ридберга при n' = 1 и n = 2, 3, 4,… Линия Lα = 1216 Å является резонансной линией водорода. Граница серии — 911,8 Å.

Серия Бальмера - Открыта И. Я. Бальмером в 1885 году. Первые четыре линии серии находятся в видимом диапазоне. Серия соответствует формуле Ридберга при n' = 2 и n = 3, 4, 5,… Линия Hα = 6565 Å. Граница серии — 3647 Å.

Серия Пашена - Предсказана Ритцем в 1908 году на основе комбинационного принципа. Открыта Ф. Пашеном в том же году. Все линии серии находятся в инфракрасном диапазоне. Серия соответствует формуле Ридберга при n' = 3 и n = 4, 5, 6,… Линия Pα = 18756 Å. Граница серии — 8206 Å.

Серия Брэккета - Открыта Ф. С. Брэккетом в 1922 году. Все линии серии находятся в ближнем инфракрасном диапазоне. Серия соответствует формуле Ридберга при n' = 4 и n = 5, 6, 7,… Линия Bα = 40522 Å. Граница серии — 14588 Å.

Серия Пфунда - Открыта А. Г. Пфундом в 1924 году. Линии серии находятся в ближнем (часть в среднем) инфракрасном диапазоне. Серия соответствует формуле Ридберга при n' = 5 и n = 6, 7, 8,… Линия Pfα = 74598 Å. Граница серии — 22794 Å.

Серия Хэмпфри - Открыта К. Д. Хэмпфри в 1953 году. Серия соответствует формуле Ридберга при n' = 6 и n = 7, 8, 9,… Основная линия 123718 Å. Граница серии — 32823 Å.

Билет № 15.

1)Характеристики волн.

Базовым представителем волн являются линейные распространяющиеся волны, возникающие в системах, динамика которых может быть описана линейными гиперболическими уравнениями второго порядка (волновыми уравнениями) относительно характеристик системы

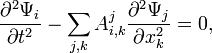
где матрицы положительно определены для всех .

Геометрические элементы

Геометрически у волны выделяют следующие элементы:

• гребень волны — множество точек волны с максимальным положительным отклонением от состояния равновесия;

• долина (ложбина) волны — множество точек волны с наибольшим отрицательным отклонением от состояния равновесия;

• волновая поверхность — множество точек, имеющих в некий фиксированный момент времени одинаковую фазу колебаний. В зависимости от формы фронта волны выделяют плоские, сферические, эллиптические и другие волны.

Терминология гребня и ложбины волны, как правило, применима к поверхностным волнам на границе двух сред – например, для поверхностных волн на воде. Иногда эту терминологию используют для описания графиков волнового процесса. Для продольных волн используются понятия экстремальных точек волны: точек максимального сжатия и максимального разрежения [3]. При этом в случае механических волн соответствующие элементарные объёмы смещаются из своих положений равновесия к области максимального сжатия или от области максимального разрежения с обеих сторон от волновых поверхностей, проходящих через экстремальные точки волны. Максимума же или минимума достигают только параметры субстанции – например, давление в элементарном объёме, концентрация определённого химического вещества, напряжённость поля, плотность элементов дискретной динамической системы и т. д.

Для стоячих волн используют понятие пучность и узел.