59. Построение модели множественной регрессии.

Она определяет форму связи, тесноту связи и степень влияния отдельных факторов на общий результат.

Коэффициент корреляции в данном случае находится по формуле:

, где r-коэффициенты корреляции между двумя признаками.

Коэффициент парной корреляции находится по формуле: :

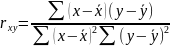
Уравнение множественной регрессии:

1. Логический анализ сущности явления и причинно-следственная связь.

2. Сборка вечной информации и проверка ее на однородность и нормальность распределения.

3. Исключение из массива информации всех резко выделяющихся единиц по уровням признака фактора (Х).

4. Установление факта наличия корреляционной зависимости между результативным и факторным признаком.

5. Оценка степени тесноты связи при помощи коэффициента корреляции и оценка ее существенности.

Множественная корреляция определяет форму связи, тесноту связи и степень влияния отдельных факторов на общий результат.

Изменяется от 0 до 1.

60. Способы оценки полученных моделей регрессии (основные критерии).

С целью наилучшего восстановления по исходным статистическим данным условного значения результатирующего показателя у(х) и неизвестной функции регрессии f(x) = M(y/x) наиболее часто используют следующие критерии адекватности (функции потерь).

1. Метод наименьших квадратов, согласно которому минимизируется квадрат отклонения наблюдаемых значений результативного показателя yi(i=1,2,…,n) от модельных значений i = f(xi, b), где b = (b0, b1,…,bk)- коэффициенты уравнения регрессии, xi – значение вектора аргументов в i-м наблюдении:

2. Метод наименьших модулей, согласно которому минимизируется сумма абсолютных отклонений наблюдаемых значений результативного показателя от модульных значений  = f(xi, b).

3. Метод минимакса сводится к минимизации максимума модуля отклонения наблюдаемого значения результативного показателя yi от модельного значения f(xi, b).

61. Мультиколлинеарность и способы ее устранения.

Мультиколлинеарность - тесная связь между факторными признаками, включается в модель. Она возникает, если:1. Факторные признаки характеризуют одну и ту же сторону явления; 2. В качестве факторов используются показатели, суммарное значение которых представляет собой постоянную величину. 3. Факторные признаки дублируют друг друга или являются составными элементами друг друга.

К основным способам устранения мультиколлинеарности в модели множественной регрессии относятся: http://www.be5.biz/ekonomika/e011u/38.htm

1) способ преобразования переменных, например, вместо значений всех переменных, участвующих в модели (и результативной в том числе) можно взять их логарифмы:

lny=β0+β1lnx1+β2lnx2+ε.

Однако данный способ также не способен гарантировать полного устранения мультиколлинеарности факторов;

Если ни одну из факторных переменных, включённых в модель множественной регрессии, исключить нельзя, то применяют один из основных смещённых методов оценки коэффициентов модели регрессии – гребневую регрессию или ридж (ridge).

При использовании метода гребневой регрессии ко всем диагональным элементам матрицы (ХТХ) добавляется небольшое число τ: 10-6 ‹ τ ‹ 0.1. Оценивание неизвестных параметров модели множественной регрессии осуществляется по формуле:

где ln – единичная матрица.

Результатом применения гребневой регрессии является уменьшение стандартных ошибок коэффициентов модели множественной регрессии по причине их стабилизации к определённому числу.

Метод главных компонент является одним из основных методов исключения переменных из модели множественной регрессии.

Данный метод используется для исключения или уменьшения мультиколлинеарности факторных переменных модели регрессии. Суть метода заключается в сокращении числа факторных переменных до наиболее существенно влияющих факторов. Это достигается с помощью линейного преобразования всех факторных переменных xi (i=0,…,n) в новые переменные, называемые главными компонентами, т. е. осуществляется переход от матрицы факторных переменных Х к матрице главных компонент F.

Метод пошагового включения переменных состоит в выборе из всего возможного набора факторных переменных именно те, которые оказывают существенное влияние на результативную переменную.