56. Виды связей и зависимостей признаков.

По характеру зависимости признаков различают функциональную (полную) связь и корреляционную (статистическую, неполную) связь.

Функциональная зависимость (жестоко детерминированная у=2х) – величине факторного признака строго соответствует одно или несколько значений результативного признака.

Статистическая – определенному значению факторного признака соответствует лишь среднее значение результативного признака. Стат. Связь не имеет ограничений и условий как в функциональной. Корреляционная связь является частным случаем стат. связи состоит в том, что разным значениям одной переменной соответствуют различные средние значения др. Цель – определение тесноты, направления связи и определение роли систематической вариации в общей вариации

Виды статистической связи.

1. По направлению связи: Положительная (прямая) – с увеличением (уменьш) одного признака в основном увелич. (уменьш) значения другого. Отрицательная (обратная) – с увеличением (уменьш) одного признака в основном уменьшаются (увеличив) значения другого.

2. Относительно своей аналитической формы:

Линейная – между признаками в среднем проявляются линейные соотношения.

Нелинейная – выражается нелинейной функцией, а переменные связаны между собой в среднем нелинейно.

3. С точки зрения взаимодействующих факторов.

Парная – характеризуется связь 2 признаков.

Множественная – изучаются более чем 2 переменные.

57. Корреляционный анализ (показатели).

Статистическая – определенному значению факторного признака соответствует лишь среднее значение результативного признака. Стат. Связь не имеет ограничений и условий как в функциональной. Более важным частным случаем статистической зависимости является корреляционная зависимость, характеризующая взаимосвязь значений одних случайных величин со средним значением других.

Если же у взаимосвязанных величин вариацию имеет только одна переменная, а другая является детерминированной, то такую связь называют не корреляционной, а регрессионной.

При прямой связи y=a0+a1x, где

A0- свободный член, а1 – коэффициент регрессии, который показывает насколько в среднем отклоняется величина результативного признака при отклонении величины факторного признака на единицу.

Должна быть решена система:

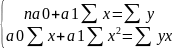
Теснота связи оценивается при помощи парного коэффициента корреляции:

Изменение от -1 до 1 – парный коэффициент корреляции

Если отрицательный - связь обратная

Если положительный – прямая

Если связь криволинейная, то уравнение будет: y=a0+a1x+a2 ,

где а2 – показывает степень ускорения или замедления кривизны параболы.

При этой связи используют индекс корреляции:

У- теоретическое выровненное значение.

58. Построение модели парной регрессии.

Парная  регрессия характеризует связь между двумя признаками - результативным и факторным. Аналитическая связь между ними описывается следующими уравнениями:

прямой  y=kx+b

гиперболы y=k/x+b

параболы y=ax^2+bx+c

 

     Определить  тип уравнения можно, исследуя зависимость  графически. Однако существуют более  общие указания, позволяющие выявить уравнение связи, не прибегая к графическому изображению. Если результативный и факторный признаки возрастают одинаково, примерно в арифметической прогрессии, то это свидетельствует о том, что связь между ними линейная, а при обратной связи - гиперболическая. Если факторный признак увеличивается в арифметической прогрессии, а результативный - значительно быстрее, то используется связь параболическая или степенная.

1. Логический анализ сущности явления и причинно-следственная связь.

2. Сборка вечной информации и проверка ее на однородность и нормальность распределения.

3. Исключение из массива информации всех резко выделяющихся единиц по уровням признака фактора (Х).

4. Установление факта наличия корреляционной зависимости между результативным и факторным признаком.

5. Оценка степени тесноты связи при помощи коэффициента корреляции и оценка ее существенности.