2.7 Расчет наклонных сечений панели на поперечную силу

_{Исходные данные для расчета:}

Продольные ребра армированы плоскими каркасами с поперечными стержнями из арматуры класса В500 (R_sw = 300 МПа) и продольными (верхним и нижним) стержнями каркаса из 8 А400 (R_s = 355 МПа).

Примем предварительно диаметр поперечных стержней равным 6 мм (при двух поперечных стержнях в сечении панели = 2∙28,3 = 56,6 мм²), а шаг поперечных стержней на приопорных участках равным = 150 мм, что меньше 0,5h₀ = 0,5335 = 167,5 мм

Тогда при заданном поперечном армировании расчет прочности наклонных сечений сводится к проверке несущей способности.

1. Проверяем условие прочности по бетонной полосе

Q = 115,34 кН < 0,3R_bbh₀ = 0,319,5185335 = 362,554 кН – условие выполняется.

2. Вычисляем параметры, необходимые для проверки условия прочности:

= мм, что больше принятого шага = 150 мм; 1,5∙1,38∙1,30∙185∙335² =55,87∙10^{6 Н∙мм;}

Q_b,max = 2,5R_btbh₀ = 2,5∙1,30∙185∙335 = 201418,75 Н;

Q_b,min = 0,5_nR_btbh₀ = 0,5∙1,38∙1,30∙185∙335 =55592,04 Н;

=

по условию

q_sw = 94,38 Н/мм > 0,25_n R_bt b = 0,25∙1,38∙1,30∙185 = 82,97 Н/мм, следовательно, хомуты учитываются в расчете;

q₁ = q - 0,5ν = 33,19 – 0,5∙26,33 = 20,025 кН/м;0

= =

= =

= > = 807,23 мм.

Т.к С=1670,33мм > h₀ = 3∙335=1005мм

Поперечная сила 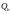, воспринимаемая бетоном:

= = Q_b,min = 55592,04 Н,

поэтому принимаем = Q_b,min = 55,592 кН.

Поперечная сила Q_sw, воспринимаемая хомутами в наклонном сечении с длиной горизонтальной проекции с₀ = 2h₀ = 2∙335 = 670 мм

Q_sw = 0,75 q_sw c₀ = 0,75∙113,2∙670 = 56883 Н = 56,883 кН.

Поперечная сила Q в нормальном сечении, проходящем на расстоянии с = 1005 мм от опоры

Q = Q_max – q₁c = 115,34 – 20,0255∙1,005 95,215 кН.

3. Проверяем условие прочности

Q = 95,215 кН < + Q_sw = 55,592 + 56,883 = 112,475 кН;

условие удовлетворяется. Следовательно, принятые диаметр и шаг поперечных стержней обеспечивают прочность наклонных сечений панели при действии поперечных сил.

Согласно п. 5.2.1 [3] у концов предварительно напряженных элементов на длине не менее 0,6 длины зоны передачи предварительного напряжения l_p следует предусматривать установку дополнительной поперечной или косвенной арматуры, охватывающей напрягаемую арматуру.

Длина зоны передачи напряжений

где = 679 МПа – предварительное напряжение с учетом первых потерь;

= 22 мм – диаметр напрягаемых стержней;

= = 2,51,30 = 3,25 МПа (здесь  = 2,5 для горячекатаной и термомеханически упрочненной арматуры класса А).

Тогда у концов продольных ребер на длине 0,6l_p = 0,61149,08 = 689,45 мм устанавливаем дополнительную поперечную арматуру в виде U-образных сеток из проволоки 5 В500 с шагом стержней 100 мм; эти сетки охватывают напрягаемую арматуру и ставятся на всю высоту продольного ребра.

2.8 Расчет полки на местный изгиб

При отсутствии поперечных ребер полка работает как балочная плита на изгиб в коротком направлении, т. е. между продольными ребрами. Для расчета из полки вырезается полоса шириной которая рассматривается как балка пролетом частично защемленная в продольных ребрах.

Расчетный пролет полки в свету между продольными ребрами

Погонная нагрузка на полосу шириной численно равна распределенной по площади, т.е. (табл.1).

Изгибающий момент в полке с учетом ее частичной заделки в продольные ребра (т.е. с учетом возможности поворота опорных сечений)

Арматуру полки подбираем как для изгибаемого элемента прямоугольного профиля размером с рабочей высотой сечения

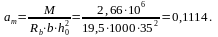
Требуемая площадь сечения рабочих стержней на 1 м ширины полки

Принимаем шаг рабочих поперечных стержней 100 мм, Ø5 В500, тогда площадь их сечения на 1 м ширины полки составит

Продольные стержни полки приняты из проволоки Ø5 В500 с шагом 200 мм.

При наличии поперечных ребер характер работы полки меняется: полка работает на изгиб в двух направлениях по схеме неразрезной (однорядной) плиты, опертой по контуру. Пролетные и опорные изгибающие моменты в обоих направлениях определяют по методу предельного равновесия из уравнения XI.39 [8] или 6.127 [6], полученного в предположении конвертообразной схемы разрушения плиты; там же приведены и рекомендации по армированию таких плит.