6. Шкали відношень
Нехай
величини, що спостерігаються, задовольняють
аксіомам тотожності 1-3, аксіомам
упорядкованості 4, 5, а також аксіомам
адитивності:
6.Якщо
А = РіВ>0,
то
А
+ В>Р.
7.А
+ В = В + А.
8.Якщо
А = РіВ
=Q,то
А
+
В = Р + Q.
9.(А
+ В) + С = А + (В + С).
Результати
таких вимірювань є повноцінними числами
й з ними можна виконувати будь-які
арифметичні операції. Відповідна шкала
називається шкалою
відношень.
При її побудові використовується
природний (абсолютний) нуль, однак
зберігається свобода у виборі одиниці
вимірювань. Зв'язок між значеннями
вимірів однієї й тієї самої величини у
двох різних шкалах відношень є прямо
пропорційним:
у
= ах(а≠0).
Відповідно, відношення
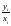 для будь-якого виміру не залежить від
обраної шкали. Прикладами
величин, що вимірюють у шкалі відношень,
є маса, електричний заряд, кінетична
енергія, гроші й таке інше.
для будь-якого виміру не залежить від
обраної шкали. Прикладами
величин, що вимірюють у шкалі відношень,
є маса, електричний заряд, кінетична
енергія, гроші й таке інше.
Питання.
Як Ви вважаєте, чи є абсолютна шкала
температур Кельвіна шкалою відношень?
7. Абсолютна шкала
Абсолютна
шкала має
абсолютний нуль і абсолютну одиницю
виміру. Її прикладом
може бути числова вісь. Важливою
особливістю такої шкали є безрозмірність
її одиниці. Це дає змогу не тільки
виконувати з показаннями абсолютної
шкали всі арифметичні операції, а й
використовувати їх як показники
ступеневої функції, а також аргументи
показникової та логарифмічної функцій.


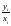 для будь-якого виміру не залежить від
обраної шкали. Прикладами
величин, що вимірюють у шкалі відношень,
є маса, електричний заряд, кінетична
енергія, гроші й таке інше.
для будь-якого виміру не залежить від
обраної шкали. Прикладами
величин, що вимірюють у шкалі відношень,
є маса, електричний заряд, кінетична
енергія, гроші й таке інше.