8.2. Дисперсионный анализ
Задачей дисперсионного анализа является исследование влияния различных факторов на изменчивость средних значений наблюдаемых случайных величин. План дисперсионного анализа предполагает проведение эксперимента, позволяющее разложить сложную дисперсию на составляющие. Далее полученные дисперсии оцениваются по определенному критерию. Наиболее удобно и оправдано сравнивать полученные дисперсии с ошибкой опытных данных, которую получают по параллельным опытам на каждом уровне факторов.
Однофакторный эксперимент предполагает выяснить влияние фактора А на выходную переменную у. Результаты наблюдений представляют моделью:
(j
= 1, 2, …, m,
i
= 1, 2, …, p)
(43)
где
– суммарный эффект во всех опытах
(среднее значение); αi
– эффект фактора А на i-том
уровне; еij
– ошибка измерения на i-том
уровне;
m
–
число параллельных опытов; р
– число уровней фактора А.
При условии выполнения нормального закона (закона распределения Гаусса) при N измерениях одинаковой точности среднее арифметическое из результатов, полученных при всех измерениях, является наиболее вероятным и наилучшим значением измеряемой величины:
(44)
Рассеяние результатов измерений относительно среднего значения принято характеризовать дисперсией S2:
(45)
или стандартным отклонением – S:
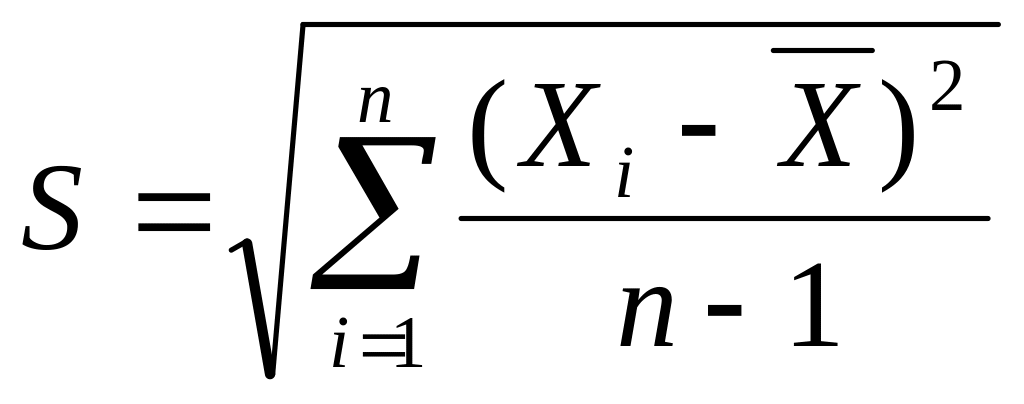(46)
которое обычно и приводят при представлении результатов измерений и которым характеризуют их воспроизводимость. При оценке воспроизводимости полученных результатов вычисляют также дисперсию среднего арифметического:
(47)
и стандартное отклонение среднего арифметического:
(48)
Однородность дисперсий на каждом уровне фактора А можно проверить по критерию Кохрена, расчетное значение которого определяют по уравнению:
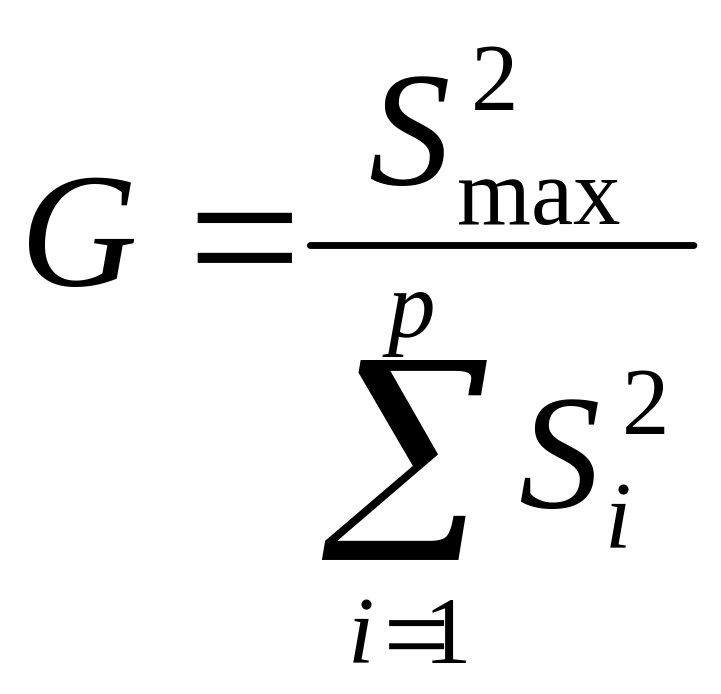(49)
где
S2max
– максимальная из рассчитанных дисперсий
параллельных опытов;
– сумма всех дисперсий по уровням
фактора А.
8.3. Регрессионный анализ
По результатам эксперимента над объектом исследования, входы и выходы которого известны, можно получить математическую модель определенного вида. Полученная математическая модель (если это полином определенной степени) называется уравнением регрессии.
Степень приближения уравнения регрессии к реальному объекту зависит не только от экспериментальных данных, но и от метода построения полинома. В качестве такого метода обычно выбирают метод наименьших квадратов, являющийся частным случаем метода максимума правдоподобия для случайных переменных с нормальным распределением. Уравнение регрессии, полученное по методу наименьших квадратов, подвергается статистическому анализу, основанному на оценках дисперсий: проверяется однородность дисперсий, значимость коэффициентов и адекватность уравнения регрессии. Это и есть регрессионный анализ.
В основе регрессионного анализа лежит несколько статистических предпосылок, выполнение которых гарантирует достоверность анализа полученной математической модели:
1. Выходная переменная – случайная величина с нормальным распределением; факторы – суть неслучайные величины; практически это означает, что ошибки в управлении факторами по крайней мере на порядок меньше ошибок при измерении выходной переменной.
2. Связь между факторами отсутствует.
3. Дисперсии выходной переменной однородны (равноточны) в любой точке факторного пространства.
4. Исследуемый объект лишен динамических свойств (рассматриваются стационарные режимы объекта).