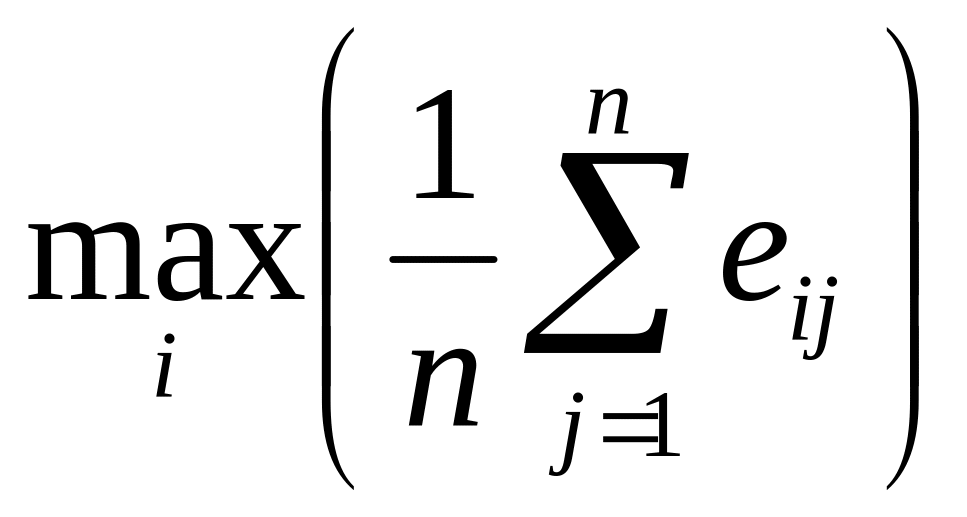- •Введение
- •1. Структура системы экологического контроля. Объекты, цели и задачи экологического контроля
- •Контрольные вопросы
- •2.2. Качество и охрана природной среды
- •2.2.1. Классификация и формы загрязнения окружающей среды
- •2.2. Экологическая служба промышленного предприятия
- •2.3. Содержание инструкции о порядке организации экологического контроля на конкретном предприятии
- •2.4. Характеристика предприятий в зависимости от категории опасности
- •2.5. Комплексная оценка эффективности функционирования систем экологического контроля на промышленных предприятиях
- •2.6. Количественная и качественная оценка эффективности систем экологического контроля
- •Контрольные вопросы
- •3. Критерии оценки состояния окружающей среды и производственных процессов
- •3.1. Методы контроля качества окружающей среды
- •Методы исследований окружающей среды
- •3.2. Критерий экологичности технологических процессов
- •3.3. Математическая модель оценки степени экологичности производства
- •3.4. Практические подходы к последовательному снижению отрицательного воздействия производства на окружающую среду и минимизации использования ресурсов
- •Контрольные вопросы
- •4. Анализ риска загрязнения окружающей среды
- •4.1. Положения анализа риска
- •Порядок рассмотрения проблемы риска
- •4.2. Основная формальная структура принятия решений
- •Принятие решений по оценочной функции
- •4.3. Классические критерии принятия решений
- •4.4. Производные критерии принятия решений
- •4.5. Количественные характеристики ситуации принятия решений
- •4.6. Основы анализа риска с помощью дерева отказа
- •Компоненты построения дерева отказа
- •Символы событий
- •Контрольные вопросы
- •5. Регулирование воздействия на окружающую среду
- •5.1. Нормативные и качественные показатели окружающей природной среды
- •Система норм и нормативов
- •5.1. Экономический механизм охраны окружающей среды
- •5.2. Ответственность за нарушение природоохранительного законодательства, норм по охране окружающей среды
- •5.3. Экологические функции правоохранительных органов
- •Контрольные вопросы
- •6. Экологический паспорт промышленного предприятия
- •6.1. Назначение и содержание экологического паспорта
- •6.2. Взаимодействие в системе «промышленное предприятие – окружающая среда»
- •Контрольные вопросы
- •Экологическая сертификация
- •Контрольные вопросы
- •Планирование промышленного эксперимента
- •8.1. Критерии оптимальности и типы планов
- •8.2. Дисперсионный анализ
- •8.3. Регрессионный анализ
- •8.4. Постановка задачи оптимизации
- •8.5. Полный факторный эксперимент первого порядка
- •Матрица планирования полного факторного эксперимента
- •8.6. Оценки коэффициентов функции отклика
- •8.7. Дробный факторный эксперимент
- •8.8. Оценки коэффициентов функции отклика в дробном факторном эксперименте
- •8.9. Проверка значимости оценок коэффициентов модели
- •8.10. Планы для описания поверхности отклика
- •Матрицы планирования трехфакторного эксперимента
- •8.11. Планы для оценки влияния факторов
- •Контрольные вопросы
- •Библиографический список
- •1. Экология горного производства: Учебник для вузов / Мирзаев г.Г., Иванов б.А., Щербаков в.М., Проскуряков н.М. – м.: Недра, 1991. – 320 с.
Принятие решений по оценочной функции
Номер уравнения |
Оценочная функция |
Оценка решения |
15 |
|
|
14 |
|
|
16 |
|
|
13 |
|
|
Оценочные функции всегда должны выбираться с учетом количественных характеристик ситуации, в которой принимаются решения.
4.3. Классические критерии принятия решений
Минимаксимальный критерий (ММ-критерий) использует оценочную функцию (15), которая соответствует позиции крайней осторожности (пессимистическая позиция). В этом случае надо ориентироваться на наименее благоприятный случай и приписывать каждому из альтернативных вариантов наихудший из возможных результатов. После этого выбирается самый выгодный вариант, т.е. ожидается наилучший результат в наихудшем случае. Для каждого иного внешнего состояния результат может быть только равным этому или лучшим.
При
![]() ;
(17)
;
(17)
![]() (18)
(18)
справедливо соотношение
![]() ,
(19)
,
(19)
где ZMM – оценочная функция ММ-критерия.
Таким образом, множество Ео оптимальных вариантов состоит из тех вариантов Eio, которые принадлежат множеству Е всех вариантов и оценка еio которых максимальна среди всех оценок .
Применение ММ-критерия бывает оправдано, если ситуация, в которой принимается решение, характеризуется следующими обстоятельствами:
о возможности появления внешних состояний ничего не известно;
приходится считаться с появлением различных внешних состояний;
необходимо исключить какой бы то ни было риск, т.е. ни при каких условиях внешнего состояния не допускается получить результат меньший, чем ZММ.
При построении оценочной функции ZММ каждый вариант Еi представлен лишь одним из своих результатов . Критерий Байеса-Лапласа (BL-критерий), напротив, учитывает каждое из возможных следствий. Пусть рj – вероятность появления внешнего состояния Fj. Тогда для BL-критерия можно записать
![]() ;
(20)
;
(20)
![]() (21)
(21)
![]() .
(22)
.
(22)
Таким
образом, множество Eo
оптимальных вариантов состоит из
вариантов Eio,
которые принадлежат множеству Е
всех вариантов и оценка которых eio
максимальна среди всех оценок
![]() при условии, что
при условии, что
![]() .
.
Исходная позиция применяющего BL-критерий, оптимистичнее, чем позиция применяющего ММ-критерий, однако такая позиция предполагает более высокий уровень информированности и достаточно длинные реализации.
Критерий Сэвиджа (S-критерий) вводится соотношением вида
![]() .
(23)
.
(23)
С помощью обозначений
![]() ;
(24)
;
(24)
![]() (25)
(25)
формируется оценочная функция
![]() (26)
(26)
и строится множество оптимальных вариантов решения
![]() .
(27)
.
(27)
Следовательно, множество Ео оптимальных вариантов состоит из тех вариантов Eoi, которые принадлежат множеству Е всех вариантов и оценка eio которых минимальна среди всех оценок eir.