Міністерство освіти та науки України

Дніпропетровський національний університет

імені Олеся Гончара

Фізико-Технічний факультет

Курсова робота за темою

„ ”

Розробка програми на алгоритмічній

мові Фортрану

з курсу

Інформатика

Виконав:

Студент групи

ТД-12-1

Майдабура А.А.

Перевірив:

Доцент: Золотко К.Є.

Дніпропетровськ

2013

Зміст

Вступ

1. Постановка задачі

2. Математичний опис методу

2.1 Алгоритм

3. Практична частина Фортран

3.1 Структурна схема програми

3.2 Чисельний експеримент

3.3 Опис програми

3.4 Оператори

4. Методи розв’язання системи лінійних рівнянь

4.1 Метод Крамера

4.2 Метод Гауса

4.3 Матричний метод

5. Практична частина Excel

5.1 Метод Крамера

5.2 Метод Гауса

5.3 Матричний метод

Постановка задачі

Математичний розділ методу

Опис програми на алгоритмічній мові Фортрану

Чисельний експеримент

Висновки

Список використаної літератури

1. Постановка задачі

1. Написати програму на алгоритмічній мові Фортран для вирішення рівняння.

2. Розв’язати рівняння у Mathcad всіма методами та побудувати графік.

3. Розв’язати систему лінійних рівнянь в Excel та Mathcad

Завдання до пунктів 1,2:

Рівняння: x³-x²+3=0

Метод для Фортрану: Дотичних

Завдання до пункті 3:

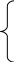
-4x₁-8x₃-4x₄-4=0

6x₁-2x₂-6x₃-6x₄-18=0

-4x₁+2x₂-8x₃-8x₄+2=0

-8x₂-6x₃-8x₄-30=0

2. Математичний опис методу Метод Ньютона (метод дотичних)

Нехай корінь ξ рівняння f(x)=0 відділений на відрізку [a,b]. Припустимо що ми знайшли (n-1)-е наближення кореня xn-1. Тоді n-е наближення xn ми можемо отримати наступним чином. Нехай

x_n = x_n-1 + h_n-1 . (1)

Розкладаючи в ряд f (x = ξ) в точці xn-1, отримаємо

f(x_n) = f(x_n-1+h_n-1) = f(x_n-1) + f’(x_n-1)h_n-1=0

Звідси випливає

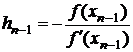. (2)

Підставимо (2) у формулу (1), отримаємо

(3)

Рис.1. Геометрична інтерпретація методу Ньютона

Геометрично метод Ньютона еквівалентний заміні дуги кривої y = f (x) дотичній, проведеної в деякій точці кривої (див. рис.1).

У точці B маємо f (x₀) f'' (x₀)> 0. Тут x₀ = b. Проведемо дотичну в точці B, отримаємо на перетині дотичної віссю OX точку x₁. Далі проводимо дотичну в точці B₁, отримаємо точку x₂ і т.д.

Якщо покласти x₀ = a, то в точці x0 будемо мати f (x₀) f'' (x₀) <0. Тоді дотична в точці A перетнула б вісь OX в точці x'₁, що лежить поза відрізка [a, b], тобто при такому виборі початкової точки, метод Ньютона виявляється розбіжним. Достатні умови збіжності методу Ньютона визначаються наступною теоремою.

Якщо f (a) f (b) <0, причому f '(x) і f'' (x) відмінні від нуля і зберігають певні знаки при a ≤ x ≤ b, то виходячи з початкового наближення , задовольняючого нерівность f (x0) f'' (x0)> 0 (4) можна обчислити методом Ньютона (3) єдиний корінь ξ рівняння f (x) = 0 з будь-яким ступенем точності.

Доказ: Нехай . Відповідно до нерівності (4) в якості точки x0 ми повинні взяти ту кордон відрізка, для якої f (x0)> 0, тобто в даному випадку т. b.

Отже, маємо x₀> ξ. Доведемо, що всі наближення x_n> ξ і отже всі f (x_n)> 0. Нехай тепер

x_n-1> ξ. Отже,

ξ = x_n-1 + (ξ-x_n-1).

Застосовуючи формулу Тейлора, отримаємо

,

де ξ <c_n-1<x_n-1.

Так як f’’(x)>0, то маємо

 і, отже

(5)

З (5) враховуючи знаки и  маємо x_n<x_n-1, тобто отримуємо обмежену монотонну спадаючу послідовність . Отже, існує .

Переходячи до межі у формулі (3) отримаємо

, тобто f (ξ) = 0, і отже, ξ-корінь.

Оцінимо швидкість збіжності методу Ньютона. З (3) випливає

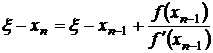. (6)

Представимо f(ξ) у вигляді

, звідси

. (7)