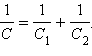- •Электрическая цепь с последовательным соединением элементов
- •Электрическая цепь с параллельным соединением элементов
- •Электрическая цепь со смешанным соединением элементов
- •Соединение элементов электрической цепи по схемам «звезда» и «треугольник»
- •12) Электроемкостью системы из двух проводников называется физическая величина, определяемая как отношение заряда q одного из проводников к разности потенциалов Δφ между ними:
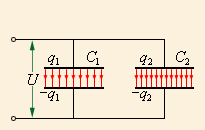
- •Таким образом, при параллельном соединении электроемкости складываются.
- •При последовательном соединении конденсаторов складываются обратные величины емкостей.
- •, Отсюда .
Таким образом, при параллельном соединении электроемкости складываются.
|
|
При
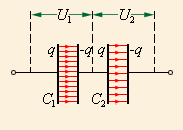
последовательном соединении (рис. 1.6.4)
одинаковыми оказываются заряды обоих
конденсаторов:q1 = q2 = q,
а напряжения на них равны 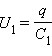 и
и 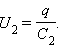 Такую
систему можно рассматривать как единый
конденсатор, заряженный зарядом q при
напряжении между обкладками U = U1 + U2.
Следовательно,
Такую
систему можно рассматривать как единый
конденсатор, заряженный зарядом q при
напряжении между обкладками U = U1 + U2.
Следовательно,
|
При последовательном соединении конденсаторов складываются обратные величины емкостей.
Формулы для параллельного и последовательного соединения остаются справедливыми при любом числе конденсаторов, соединенных в батарею.
![]()
|
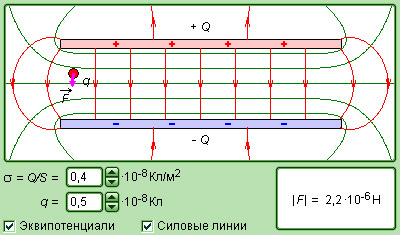
Модель. Поле плоского конденсатора |
13) см.лецию
14) см.лекцию
15) см.лекцию
16) см.лекцию
17)
Соленоид —
длинная, тонкая катушка, то есть катушка,
длина которой намного больше, чем её
диаметр (также в дальнейших выкладках
здесь подразумевается, что толщина
обмотки намного меньше, чем диаметр
катушки). При этих условиях и без
использования магнитного материала
плотность магнитного потока ![]() внутри
катушки является фактически постоянной
и (приближенно) равна
внутри
катушки является фактически постоянной
и (приближенно) равна
![]()
где ![]() − магнитная
постоянная,
− магнитная
постоянная, ![]() −
число витков,
−
число витков, ![]() −
ток и
−
ток и ![]() −
длина катушки. Пренебрегая краевыми
эффектами на концах соленоида, получим[16],
что потокосцепление через катушку равно
плотности потока
,
умноженному на площадь поперечного
сечения
−
длина катушки. Пренебрегая краевыми
эффектами на концах соленоида, получим[16],
что потокосцепление через катушку равно
плотности потока
,
умноженному на площадь поперечного
сечения ![]() и
число витков
:
и
число витков
:
![]()
Отсюда следует формула для индуктивности соленоида (без сердечника):
![]()
Если
катушка внутри полностью заполнена
магнитным материалом (сердечником), то
индуктивность отличается на
множитель ![]() — относительную
магнитную проницаемость[17] сердечника:
— относительную
магнитную проницаемость[17] сердечника:
![]()
В
случае, когда ![]() ,
можно (следует) под S понимать
площадь сечения сердечника и пользоваться
данной формулой даже при толстой намотке,
если только полная площадь сечения
катушки не превосходит площади сечения
сердечника во много раз.
,
можно (следует) под S понимать
площадь сечения сердечника и пользоваться
данной формулой даже при толстой намотке,
если только полная площадь сечения
катушки не превосходит площади сечения
сердечника во много раз.
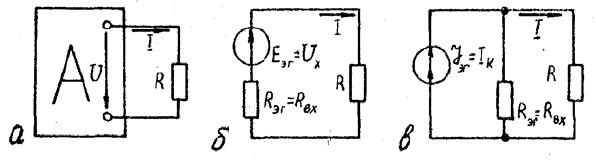
Метод эквивалентного генератора используется ля определения тока в одной (или нескольких) из ветвей сложной электрической цепи. Этот метод основан на теореме об активном двухполюснике: ток в некоторой заданной ветви не изменится, если активную цепь, к которой подключена эта ветвь, заменить источником энергии, ЭДС которого равна напряжению холостого хода на зажимах разомкнутой ветви, а его (источника) внутреннее сопротивление равно сопротивлению пассивной цепи относительно зажимов искомой ветви (рис. 1).
 Рис
1. а – активный двухполюсник, б – ЭГ как
источник ЭДС (напряжения), в – ЭГ как
источник тока.
Если
эквивалентный генератор представляется
источником ЭДС, ток в заданной ветви
определяется по закону Ома (рис.
1,6):
Рис
1. а – активный двухполюсник, б – ЭГ как
источник ЭДС (напряжения), в – ЭГ как
источник тока.
Если
эквивалентный генератор представляется
источником ЭДС, ток в заданной ветви
определяется по закону Ома (рис.
1,6):
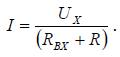 Если эквивалентный
генератор представляется
источником тока, ток в заданной ветви
находится по правилу "чужого
сопротивления" (рис. 1,в):
Если эквивалентный
генератор представляется
источником тока, ток в заданной ветви
находится по правилу "чужого
сопротивления" (рис. 1,в):
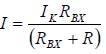 В
формулах Uх - напряжение холостого хода
активного двухполюсника на зажимах
ветви, в которой определяется ток; Iк -
ток короткого замыкания активного
двухполюсника при закороченной заданной
ветви; Rвх - входное сопротивление
пассивного двухполюсника, найденное
относительно зажимов заданной ветви;
R - сопротивление заданной ветви. Выбор
схемы замещения эквивалентного
генератора определяется схемой цепи,
в которой рассчитывается ток. Если в
заданной ветви, кроме резистора, есть
источник ЭДС и для расчета используется
последовательная схема замещения
эквивалентного генератора ( рис. 1,6),
ток можно определить из выражения
В
формулах Uх - напряжение холостого хода
активного двухполюсника на зажимах
ветви, в которой определяется ток; Iк -
ток короткого замыкания активного
двухполюсника при закороченной заданной
ветви; Rвх - входное сопротивление
пассивного двухполюсника, найденное
относительно зажимов заданной ветви;
R - сопротивление заданной ветви. Выбор
схемы замещения эквивалентного
генератора определяется схемой цепи,
в которой рассчитывается ток. Если в
заданной ветви, кроме резистора, есть
источник ЭДС и для расчета используется
последовательная схема замещения
эквивалентного генератора ( рис. 1,6),
ток можно определить из выражения
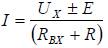 ЭДС
Е учитывается с положительным (
отрицательным) знаком, если напряжение
Uх
и
ЭДС Е совпадают (противоположны) по
направлению.
Определение
тока в заданной ветви электрической
цепи методом эквивалентного генератора
удобно производить в следующей
последовательности:
1.
Разомкнуть (или закоротить – в случае
с ЭГ с источником тока) заданную ветвь
с искомым током.
2.
Определить напряжение холостого хода
(ток короткого замыкания – в случае с
ЭГ с источником тока) активного
двухполюсника относительно заданной
ветви.
3.
Исключая из активного двухполюсника
все источники энергии, определить
входное сопротивление двухполюсника
относительно зажимов заданной ветви.
При
исключении
источников в схеме должны быть сохранены
их внутренние сопротивления.
4.
Используя закон Ома (правило " чужого
сопротивления"), найти ток в заданной
ветви. Направление тока определяется
направлением напряжения холостого
хода /тока короткого замыкания"/
ЭДС
Е учитывается с положительным (
отрицательным) знаком, если напряжение
Uх
и
ЭДС Е совпадают (противоположны) по
направлению.
Определение
тока в заданной ветви электрической
цепи методом эквивалентного генератора
удобно производить в следующей
последовательности:
1.
Разомкнуть (или закоротить – в случае
с ЭГ с источником тока) заданную ветвь
с искомым током.
2.
Определить напряжение холостого хода
(ток короткого замыкания – в случае с
ЭГ с источником тока) активного
двухполюсника относительно заданной
ветви.
3.
Исключая из активного двухполюсника
все источники энергии, определить
входное сопротивление двухполюсника
относительно зажимов заданной ветви.
При
исключении
источников в схеме должны быть сохранены
их внутренние сопротивления.
4.
Используя закон Ома (правило " чужого
сопротивления"), найти ток в заданной
ветви. Направление тока определяется
направлением напряжения холостого
хода /тока короткого замыкания"/
РАБОТА ПОСТОЯННОГО ТОКА
Рассмотрим произвольный участок цепи, к концам которого приложено напряжение U. За время dt через каждое сечение проводника проходит заряд
![]()
При этом силы электрического поля, действующего на данном участке, совершают работу:
![]()
Разделив работу на время, получим выражение для мощности:
|
|
(7.7.1) |
|
Полезно вспомнить и другие формулы для мощности и работы:
|
|
(7.7.2) |
|
|
|
(7.7.3) |
|
при протекании тока, в проводнике выделяется количество теплоты:
21)
![]()
(7.7.4)
![]()
(17.13)
Соотношение
(17.13) выражает закон Джоуля-Ленца в
интегральной форме. Введем плотность
тепловой мощности ![]() ,
равную энергии выделенной за единицу
время прохождения тока в каждой единице
объема проводника
,
равную энергии выделенной за единицу
время прохождения тока в каждой единице
объема проводника
![]()
где
S - поперечное сечение проводника, ![]() -
его длина. Используя (1.13) и соотношение
-
его длина. Используя (1.13) и соотношение ![]() ,
получим
,
получим
![]() Но
Но ![]() -
плотность тока, а
-
плотность тока, а ![]() ,
тогда
,
тогда
![]()
с
учетом закона Ома в дифференциальной
форме ![]() ,
окончательно получаем
,
окончательно получаем
|
(17.14) |
Формула (17.14) выражает закон Джоуля-Ленца в дифференциальной форме: объемная плотность тепловой мощности тока в проводнике равна произведению его удельной электрической проводимости на квадрат напряженности электрического поля.
Теорема Телледжена является одной из наиболее общих теорем теории электрических цепей. Рассмотрим граф произвольной электрической цепи, содержащей nВ ветвей и пу узлов. Для согласованных направлений напряжений и токов ветвей теорема Телледжена гласит: сумма произведений напряжений uk и токов ik всех ветвей графа, удовлетворяющих законам Кирхгофа, равна нулю.

так как выражения, стоящие в скобках, равны нулю согласно ЗТК, что и доказывает теорему. Необходимо подчеркнуть, что поскольку теорема Телледжена следует непосредственно из законов Кирхгофа, то она справедлива для любых электрических цепей: линейных и нелинейных, активных и пассивных; цепей, параметры которых изменяются во времени{параметрических цепей). В общем случае эта теорема справедлива и для случая попарных произведений иk и il разных ветвей, если для них выполняются ЗНК и ЗТК.
Из теоремы Телледжена вытекает ряд следствий, важнейшим из которых является баланс мощности. Действительно, произведение Ukik согласно формуле (1.5) представляет собой мгновенную мощность pk k-ветви, поэтому в соответствии с (1.35) алгебраическая сумма мощностей всех ветвей цепи равняется нулю. Если в (1.35) выделить ветви с независимыми источниками, то баланс мощности можно сформулировать следующим образом: алгебраическая сумма мощностей, отдаваемых независимыми источниками, равняется алгебраической сумме мощностей, потребляемых остальными ветвями электрической цепи.
Пример. Составить баланс мощности для цепи, изображенной на рис. 1.23. Алгебраическая сумма мгновенных мощностей, развиваемых источниками на-
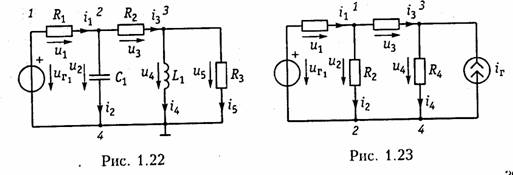
пряжения
и тока ![]() Потребляемая
мощность с учетом закона Ома
Потребляемая
мощность с учетом закона Ома
![]()
В соответствии с балансом мощностей
![]()
Следует отметить, что при определении рпсТ произведение щг берется со знаком «+», если направления задающего напряжения иТ и тока i направлены навстречу друг другу, и со знаком «—» в противном случае. Аналогичное правило знаков для источников тока: если напряжение на зажимах источника направлено навстречу задающему току гг, берется знак «+», а если напряжение совпадает с током — знак «—». Баланс мощности выражает не что иное, как закон сохранения энергии в электрической цепи.
На рис. 1.17 условно изображены идеальный источник, подключенный к началу линии, сопротивления линии и нагрузки. При этом приняты следующие обозначения:
U1 – напряжение в начале линии;
U2 – напряжение на нагрузке;
R – сопротивление проводов линии;
Rн – сопротивление нагрузки.
При передаче больших мощностей (десятки мегаватт) по реальным линиям КПД составляет 94 – 97 %, а U2 лишь на несколько процентов меньше напряжения в начале линии, что является важным с точки зрения повышения экономичности передачи мощности.
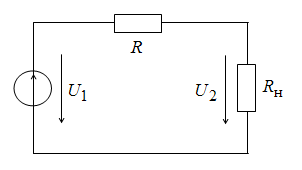
Рис. 1.17. Подключение нагрузки к источнику
Общая картина передачи мощности (рис. 1.18) может быть построена по следующим выражениям:
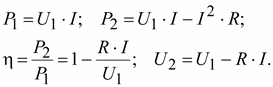
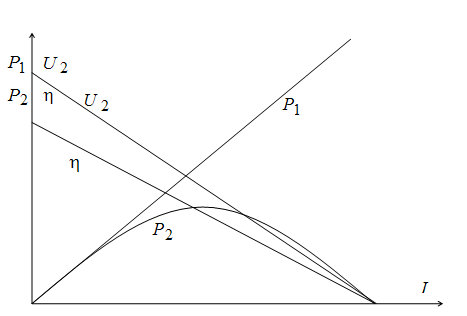
Рис.
1.18. Зависимости ![]() при
передаче энергии
при
передаче энергии
Гармонические колебания и их характеристики
Колебаниями называются
движения или процессы, которые
характеризуются определенной
повторяемостью во времени. Колебания
широко распространены в окружающем
мире и могут иметь самую различную
природу. Это могут быть механические
(маятник), электромагнитные (колебательный
контур) и другие виды колебаний.
Свободными,
или собственными колебаниями,
называются колебания, которые происходят
в системе предоставленной самой себе,
после того как она была выведена внешним
воздействием из состояния равновесия.
Примером могут служить колебания шарика,
подвешенного на нити. (ПРИМЕРЫ
![]() )
Особую
роль в
колебательных процессах имеет простейший
вид колебаний - гармонические
колебания.Гармонические
колебания лежат в основе единого подхода
при изучении колебаний различной
природы, так как колебания, встречающиеся
в природе и технике, часто близки к
гармоническим, а периодические процессы
иной формы можно представить как
наложение гармонических колебаний.
)
Особую
роль в
колебательных процессах имеет простейший
вид колебаний - гармонические
колебания.Гармонические
колебания лежат в основе единого подхода
при изучении колебаний различной
природы, так как колебания, встречающиеся
в природе и технике, часто близки к
гармоническим, а периодические процессы
иной формы можно представить как
наложение гармонических колебаний.
Гармоническими колебаниями называются такие колебания, при которых колеблющаяся величина меняется от времени по закону синуса или косинуса. Уравнение гармонических колебаний имеет вид:
![]() ,
где
A - амплитуда
колебаний (величина
наибольшего отклонения системы от
положения равновесия);
,
где
A - амплитуда
колебаний (величина
наибольшего отклонения системы от
положения равновесия); ![]() - круговая
(циклическая) частота. Периодически
изменяющийся аргумент косинуса
- круговая
(циклическая) частота. Периодически
изменяющийся аргумент косинуса ![]() -
называетсяфазой
колебаний.
Фаза колебаний определяет смещение
колеблющейся величины от положения
равновесия в данный момент времени t.
Постоянная φ представляет собой
значение фазы в момент времени t = 0 и
называется начальной
фазой колебания.
Значение начальной фазы определяется
выбором начала отсчета. Величина x может
принимать значения, лежащие в пределах
от -A до +A.
Промежуток времени T, через
который повторяются определенные
состояния колебательной системы,называется
периодом колебаний.
Косинус - периодическая функция с
периодом 2π, поэтому за промежуток
времени T, через который фаза колебаний
получит приращение равное 2π, состояние
системы, совершающей гармонические
колебания, будет повторяться. Этот
промежуток времени T называется периодом
гармонических колебаний.
Период
гармонических колебаний равен:
T = 2π/
.
Число
колебаний в единицу времени
называется частотой
колебаний ν.
Частота
гармонических колебаний равна:
ν = 1/T. Единица измерения частоты герц (Гц)
- одно колебание в секунду.
Круговая
частота
=
2π/T = 2πν дает число колебаний за 2π секунд.
-
называетсяфазой
колебаний.
Фаза колебаний определяет смещение
колеблющейся величины от положения
равновесия в данный момент времени t.
Постоянная φ представляет собой
значение фазы в момент времени t = 0 и
называется начальной
фазой колебания.
Значение начальной фазы определяется
выбором начала отсчета. Величина x может
принимать значения, лежащие в пределах
от -A до +A.
Промежуток времени T, через
который повторяются определенные
состояния колебательной системы,называется
периодом колебаний.
Косинус - периодическая функция с
периодом 2π, поэтому за промежуток
времени T, через который фаза колебаний
получит приращение равное 2π, состояние
системы, совершающей гармонические
колебания, будет повторяться. Этот
промежуток времени T называется периодом
гармонических колебаний.
Период
гармонических колебаний равен:
T = 2π/
.
Число
колебаний в единицу времени
называется частотой
колебаний ν.
Частота
гармонических колебаний равна:
ν = 1/T. Единица измерения частоты герц (Гц)
- одно колебание в секунду.
Круговая
частота
=
2π/T = 2πν дает число колебаний за 2π секунд.
У Кузьминой в лекциях
У Кузьминой в лекциях
У Кузьминой в лекциях
У Кузьминой
У Кузьминой
При перемещении электрических зарядов силы кулоновского взаимодействия совершают определенную работу dА. Работа, совершенная системой, определяется убылью энергии взаимодействия -dW зарядов
|
|
(5.5.1) |
|
Энергия
взаимодействия двух точечных
зарядов q1 и q2,
находящихся на расстоянии r12,
численно равна работе по перемещению
заряда q1 в
поле неподвижного заряда q2 из
точки с потенциалом ![]() в
точку с потенциалом
в
точку с потенциалом ![]() :
:

![]()
Будем считать аддитивную постоянную W0, равной нулю. В этом случае W может быть и отрицательной величиной, если q1 и q2 - заряды противоположного знака.
Аналогично
можно рассчитать энергию двух зарядов,
рассмотрев перемещение заряда q2 в
поле неподвижного зарядаq1 из
точки с потенциалом ![]() в
точку с потенциалом
в
точку с потенциалом ![]()

|
|
(5.5.2) |
|
Удобно записать энергию взаимодействия двух зарядов в симметричной форме
|
|
(5.5.3) |
|
Для системы из n точечных зарядов (рис. 5.14) в силу принципа суперпозиции для потенциала, в точке нахожденияk-го заряда, можно записать:
![]()
Здесь φk,i - потенциал i-го заряда в точке расположения k-го заряда. В сумме исключен потенциал φk,k, т.е. не учитывается воздействие заряда самого на себя, равное для точечного заряда бесконечности.
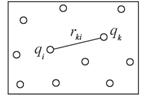
Рис. 5.14
Тогда взаимная энергия системы n зарядов равна:
|
|
(5.5.4) |
|
Данная формула справедлива лишь в случае, если расстояние между зарядами заметно превосходит размеры самих зарядов.
Сначала
замкнем соленоид L на
источник ЭДС ![]() ,
в нем будет протекать ток
,
в нем будет протекать ток ![]() .
Затем в момент времени
.
Затем в момент времени ![]() переключим
ключ в положение 2 – замкнем соленоид
на сопротивление R.
В цепи будет течь убывающий ток I.
При этом будет совершена работа:
переключим
ключ в положение 2 – замкнем соленоид
на сопротивление R.
В цепи будет течь убывающий ток I.
При этом будет совершена работа: ![]() ,
или
,
или
![]()
![]()
|
|
(5.5.1) |
|
Эта работа пойдет на нагревание проводников. Но откуда взялась эта энергия? Поскольку других изменений, кроме исчезновения магнитного поля в окружном пространстве, не произошло, остается заключить, что энергия была локализована в магнитном поле. Значит, проводник с индуктивностью L, по которой течет ток I, обладает энергией
|
|
(5.5.3) |
|
Выразим энергию магнитного поля через параметры магнитного поля. Для соленоида:
![]() .
.
![]() ;
отсюда
;
отсюда ![]()
Подставим эти значения в формулу (5.5.3):
|
|
(5.5.4) |
|
Обозначим w – плотность энергии, или энергия в объеме V, тогда
|
|
(5.5.5) |
|
но
т.к. ![]() ,
то
,
то
|
|
(5.5.6) |
|
Энергия однородного магнитного поля в длинном соленоиде может быть рассчитана по формуле
|
|
(5.5.7) |
|
а плотность энергии
|
|
(5.5.8) |
|
Плотность энергии магнитного поля в соленоиде с сердечником будет складываться из энергии поля в вакууме и в магнетике сердечника: