
- •Электрическая цепь с последовательным соединением элементов
- •Электрическая цепь с параллельным соединением элементов
- •Электрическая цепь со смешанным соединением элементов
- •Соединение элементов электрической цепи по схемам «звезда» и «треугольник»
- •12) Электроемкостью системы из двух проводников называется физическая величина, определяемая как отношение заряда q одного из проводников к разности потенциалов Δφ между ними:
- •Таким образом, при параллельном соединении электроемкости складываются.
- •При последовательном соединении конденсаторов складываются обратные величины емкостей.
- •, Отсюда .
Электрическая цепь характеризуется совокупностью элементов, из которых она состоит, и способом их соединения. Соединение элементов электрической цепи наглядно отображается ее схемой. Рассмотрим для примера две электрические схемы (рис. 1, 2), введя понятие ветви и узла.
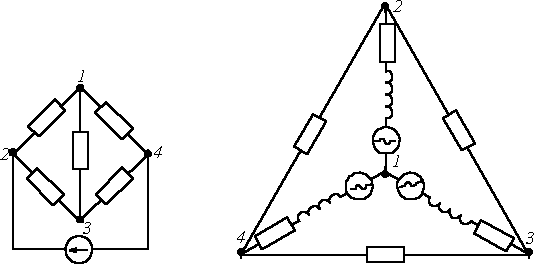
Рис.1 |
Рис.2 |
Ветвью называется участок цепи, обтекаемый одним и тем же током.
Узел – место соединения трех и более ветвей.
Представленные схемы различны и по форме, и по назначению, но каждая из указанных цепей содержит по 6 ветвей и 4 узла, одинаково соединенных. Таким образом, в смысле геометрии (топологии) соединений ветвей данные схемы идентичны.
Т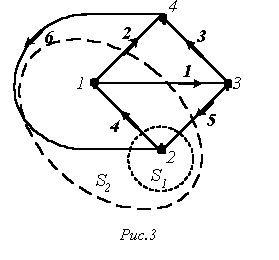 опологические
(геометрические) свойства электрической
цепи не зависят от типа и свойств
элементов, из которых состоит ветвь.
Поэтому целесообразно
каждую ветвь схемы электрической цепи
изобразить отрезком линии.
Если каждую ветвь схем на рис. 1 и 2
заменить отрезком линии, получается
геометрическая фигура, показанная на
рис. 3.
опологические
(геометрические) свойства электрической
цепи не зависят от типа и свойств
элементов, из которых состоит ветвь.
Поэтому целесообразно
каждую ветвь схемы электрической цепи
изобразить отрезком линии.
Если каждую ветвь схем на рис. 1 и 2
заменить отрезком линии, получается
геометрическая фигура, показанная на
рис. 3.
Условное изображение схемы, в котором каждая ветвь заменяется отрезком линии, называется графом электрической цепи. При этом следует помнить, что ветви могут состоять из каких-либо элементов, в свою очередь соединенных различным образом.
Отрезок линии, соответствующий ветви схемы, называется ветвью графа. Граничные точки ветви графа называют узлами графа. Ветвям графа может быть дана определенная ориентация, указанная стрелкой. Граф, у которого все ветви ориентированы, называется ориентированным.
Подграфом графа называется часть графа, т.е. это может быть одна ветвь или один изолированный узел графа, а также любое множество ветвей и узлов, содержащихся в графе.
В теории электрических цепей важное значение имеют следующие подграфы:
1. Путь – это упорядоченная последовательность ветвей, в которой каждые две соседние ветви имеют общий узел, причем любая ветвь и любой узел встречаются на этом пути только один раз. Например, в схеме на рис. 3 ветви 2-6-5; 4-5; 3-6-4; 1 образуют пути между одной и той же парой узлов 1 и 3. Таким образом, путь – это совокупность ветвей, проходимых непрерывно.
2. Контур – замкнутый путь, в котором один из узлов является начальным и конечным узлом пути. Например, для графа по рис. 3 можно определить контуры, образованные ветвями 2-4-6; 3-5-6; 2-3-5-4. Если между любой парой узлов графа существует связь, то граф называют связным.
3. Дерево – это связный подграф, содержащий все узлы графа, но ни одного контура. Примерами деревьев для графа на рис. 3 могут служить фигуры на рис. 4.
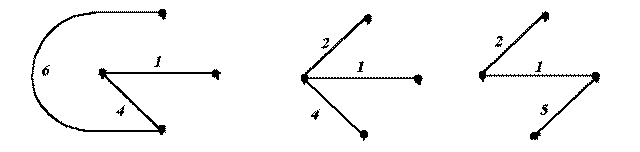
Рис.4
4. Ветви связи (дополнения дерева) – это ветви графа, дополняющие дерево до исходного графа.
Если
граф содержит m узлов
и n ветвей,
то число ветвей любого дерева ![]() ,
а числа ветвей связи графа
,
а числа ветвей связи графа ![]() .
.
5. Сечение графа – множество ветвей, удаление которых делит граф на два изолированных подграфа, один из которых, в частности, может быть отдельным узлом.
Сечение можно наглядно изобразить в виде следа некоторой замкнутой поверхности, рассекающей соответствующие ветви. Примерами таких поверхностей являются для нашего графа на рис. 3 S1 иS2 . При этом получаем соответственно сечения, образованные ветвями 6-4-5 и 6-2-1-5.
С понятием дерева связаны понятия главных контуров и сечений:
главный контур – контур, состоящий из ветвей дерева и только одной ветви связи;
главное сечение – сечение, состоящее из ветвей связи и только одной ветви дерева.
Пассивные элементы. Резистивным сопротивлением называют идеализированный элемент, обладающий только свойством необратимого рассеивания энергии. Условное обозначение резистивного сопротивления показано на рис. 1.2, а. Математическая модель, описывающая свойства резистивного сопротивления, определяется законом Ома:
![]() .
(0.6)
.
(0.6)
Коэффициенты пропорциональности R и G в формулах (1.6) называются соответственно сопротивлением ипроводимостью элемента и являются его количественной характеристикой, причем при согласованных направлениях тока и напряжения R и G положительны и связаны обратной зависимостью R=1/G. Измеряют в системе СИ сопротивление R в омах (Ом), а проводимость G – в сименсах (См).
Уравнение (1.6) определяет зависимость напряжения от тока и носит название вольт-амперной характеристики(ВАХ) резистивного сопротивления. Если R постоянно, то ВАХ линейна (рис. 1.3, а) и соответствует линейному резистивному элементу. Если же R зависит от протекающего через него тока или приложенного к нему напряжения, то ВАХ становится нелинейной (рис. 1.3, б) и соответствует нелинейному резистивному сопротивлению.
Мощность в резистивном сопротивлении можно определить согласно уравнению (1.5):

Рис. 1.3
Индуктивным элементом называют идеализированный элемент электрической цепи, обладающий только свойством накопления им энергии магнитного поля. Условное обозначение индуктивного элемента изображено на рис. 1.2, б.
Математическая модель, описывающая свойства индуктивного элемента определяется соотношением
![]() ,
(0.8)
,
(0.8)
где ![]() –
потокосцепление, характеризующее
суммарный магнитный поток, пронизывающий
катушку:
–
потокосцепление, характеризующее
суммарный магнитный поток, пронизывающий
катушку:
 ,
,
где w – число витков катушки; k – номер витка, с которым сцеплен поток Ф k. В простейшем случае, когда каждый из потоков Ф k сцеплен со всеми витками катушки =Ф w.
Коэффициент пропорциональности L в формуле (1.8) называется индуктивностью. Он имеет положительное значение и является количественной характеристикой индуктивного элемента. Измеряется индуктивность L в генри (Гн), а магнитный поток Ф – в веберах (Вб). Если величина L постоянна, то зависимость (1.8) (вебер-амперная характеристика) линейна и соответствует линейному индуктивному элементу. Если же L зависит от электрического режима (тока или напряжения), то зависимость (1.8) нелинейна и соответствует нелинейному элементу индуктивности.
Связь между током и напряжением на индуктивном элементе определяется согласно закону электромагнитной индукции выражением
![]() ,
(0.9)
,
(0.9)
т. е. напряжение на индуктивном элементе пропорционально скорости изменения протекающего через него тока. Следовательно, при протекании через L постоянного тока и=0 и свойства индуктивного элемента эквивалентны коротко замкнутому (КЗ) участку (см. рис. 1.1, а).
Емкостным элементом называют идеализированный элемент электрической цепи, обладающий только свойством накапливать энергию электрического поля. Условное обозначение емкостного элемента показано на рис. 1.2, в.
Математическая модель, описывающая свойства емкостного элемента, определяется вольт-кулонной характеристикой
![]() .
(0.11)
.
(0.11)
Коэффициент пропорциональности С в формуле (1.11) называется емкостью и является количественной характеристикой емкостного элемента. При согласованных направлениях тока и напряжения величина С всегда положительна. Измеряется С в фарадах (Ф).
Если величина С постоянная, то вольт-кулонная характеристика (1.11) линейна и соответствует линейному емкостному элементу. Если же параметр С зависит от электрического режима, то характеристика (1.11) нелинейна и соответствует нелинейному элементу.
Между током и напряжением на емкостном элементе существует связь, определяемая согласно (1.1) и (1.11) равенством
![]() ,
(0.12)
,
(0.12)
т. е. ток в емкостном элементе пропорционален скорости изменения приложенного к нему напряжения. При постоянном напряжении u=const, i=0 и емкостной элемент по своим свойствам эквивалентен разрыву цепи.
Рассмотренные идеализированные резистивный, индуктивный и емкостной элементы могут служить простейшими моделями резисторов, высококачественных катушек индуктивностей с малыми потерями и электрических конденсаторов с высокими диэлектрическими свойствами в области низких и средних частот. В области высоких, а особенно сверхвысоких частот модели резисторов, катушек индуктивности и конденсаторов становятся более сложными. Так, на высоких частотах резисторы уже нельзя с достаточной точностью описать идеальным резистивным элементом (1.6) из-за влияния различных “паразитных” емкостей. Более точной здесь будет модель
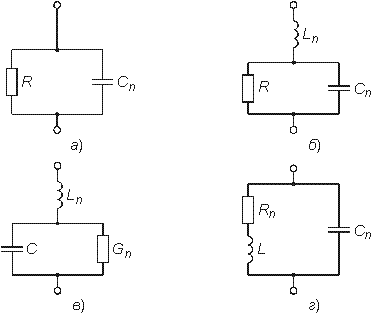
Рис. 1.4
параллельного соединения R и Сп, изображенная на рис. 1.4, а.
Рассмотренные выше резистивные, индуктивные и емкостные элементы относятся к двухполюсным, так как содержат только два зажима (полюса, вывода). Однако кроме двухполюсных элементов в теории цепей и электронике широко используются трехполюсные, четырехполюсные и многополюсные элементы.
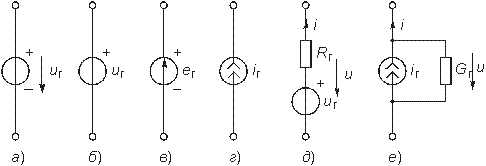
Рис. 1.5
при этом моделью трансформатора будет являться четырехполюсный элемент (см. гл. 3).
Активные элементы. Активными элементами электрической цепи являются зависимые и независимые источники электрической энергии. К зависимым источникам относятся электронные лампы, транзисторы, операционные усилители и другие, к независимым источникам – аккумуляторы, электрогенераторы, термоэлементы, пьезодатчики и другие преобразователи. Независимые источники можно представить в виде двух моделей: источника напряжения и источника тока.
Независимым источником напряжения называют идеализированный двухполюсный элемент, напряжение на зажимах которого не зависит от протекающего через него тока. Условное обозначение источника напряжения показано на рис. 1.5, а.
Источник напряжения полностью характеризуется своим задающим напряжением иг, или электродвижущей силой(ЭДС) ег (рис. 1.5, в). Внутреннее сопротивление источника напряжения равно нулю и иногда при изображении источника напряжения обозначают знаком “+” только один из зажимов и не показывают стрелкой положительное направление иг, имея в виду, что оно действует от “+” к “–” (рис. 1.5, б). Часто при анализе цепей ограничиваются изображением только зажимов источника напряжения, как показано на рис. 1.1, б.
Вольт-амперная характеристика идеального источника напряжения представляет собой прямую, параллельную оси токов (рис. 1.6, а).
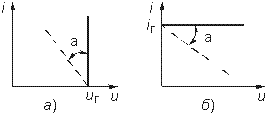
Рис. 1.6
Такой идеализированный источник способен отдавать во внешнюю цепь бесконечно большую мощность. Ясно, что физически такой источник реализовать нельзя. Однако в определенных пределах изменения тока он достаточно близко отражает реальные свойства независимых источников.
Независимым источником тока называют идеализированный двухполюсный элемент, ток которого не зависит от напряжения на его зажимах. Условное обозначение источника тока показано на рис. 1.5, г. Источник тока полностью характеризуется своим задающим током iг. Внутренняя проводимость источника тока равна нулю (внутреннее сопротивление бесконечно велико) и ВАХ представляет собой прямую, параллельную оси напряжений (рис. 1.6, б). Такой источник также способен отдавать во внешнюю цепь бесконечно большую мощность и является идеализацией реальных независимых источников.
Зависимый источник представляет собой четырехполюсный элемент (рис. 1.7) с двумя парами зажимов – входных (1,1' ) и выходных (2, 2' ). Входные ток i1 и напряжение и1 являются управляющими.
Электрическая цепь может быть разделена на два участка: внешний и внутренний. Внешний участок, или, как говорят, внешняя цепь, состоит из одного или нескольких приемников электрической энергии, соединительных проводов и различных вспомогательных устройств, включенных в эту цепь. Внутренний участок, или внутренняя цепь,— это сам источник.
Смещение
под действием электрического поля
зарядов в проводнике всегда происходит
таким образом, что электрическое поле
в проводнике исчезает и ток прекращается.
Для
протекания тока в течение продолжительного
времени на заряды в электрической цепи
должны действовать силы, отличные по
природе от сил электростатического
поля, такие силы получили название сторонних
сил.
Эти
силы могут быть обусловлены химическими
процессами, диффузией носителей тока
в неоднородной среде, электрическими
(но не электростатическими) полями,
порождаемыми переменными во времени
магнитными полями, и т. д. Всякое
устройство, в котором возникают сторонние
силы, называется источником электрического
тока.
Сторонние
силы характеризуют работой, которую
они совершают над перемещаемыми по
электрической цепи носителями
заряда. Величина,
равная работе сторонних сил по перемещению
единичного положительного заряда,
называется электродвижущей силой
(ЭДС) ![]() ,
действующей в электрической цепи или
на ее участке.
Представим
стороннюю силу
,
действующей в электрической цепи или
на ее участке.
Представим
стороннюю силу ![]() ,
действующую на заряд q, в виде
,
действующую на заряд q, в виде
![]() ,
,
где
векторная величина ![]() представляет напряженность
поля сторонних сил.
представляет напряженность
поля сторонних сил.
Математической моделью емкостного элемента С является вольт-кулоновая характеристика, которая устанавливает зависимость напряжения u от сообщенного емкости C электрического заряда q и определяется выражением:
![]() ,
или
,
или ![]() .
.

Если величина С постоянная, то вольт-кулонная характеристика (1.11) линейна и соответствует линейному емкостному элементу. Если же параметр С зависит от электрического режима, то характеристика (1.11) нелинейна и соответствует нелинейному элементу.
Вах индуктивного элемента
 Математическая
модель, описывающая свойства индуктивного
элемента определяется соотношением
Математическая
модель, описывающая свойства индуктивного
элемента определяется соотношением
, (0.8)
где – потокосцепление, характеризующее суммарный магнитный поток, пронизывающий катушку:
Если величина L постоянна, то зависимость (1.8) (вебер-амперная характеристика) линейна и соответствует линейному индуктивному элементу. Если же L зависит от электрического режима (тока или напряжения), то зависимость (1.8) нелинейна и соответствует нелинейному элементу индуктивности.
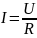 Общий закон Ома
Общий закон Ома
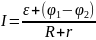 Обобщенный закон
Ома
Обобщенный закон
Ома
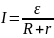 при
условии, что 1-2=0
при
условии, что 1-2=0
Для n
источников, соединенных последовательно
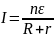
Для n
источников, соединенных параллельно
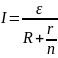
Закон Ома в диф.форме:
Закон Ома в диф.форме:
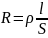
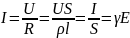
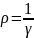
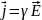

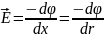

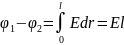
Первый закон Кирхгофа устанавливает зависимость между токами для узлов электрической цепи, к которым подходит несколько ветвей. Согласно этому закону алгебраическая сумма токов ветвей, сходящихся в узле электрической цепи, равна нулю
При этом токи, направленные к узлу, берут с одним знаком (например, положительным), а токи, направленные от узла,— с противоположным знаком (отрицательным).
Второй закон Кирхгофа устанавливает зависимость между э. д. с. и напряжением в замкнутой электрической цепи. Согласно этому закону во всяком замкнутом контуре алгебраическая сумма э. д. с. равна алгебраической сумме падений напряжения на сопротивлениях, входящих в этот контур.
При составлении формул, характеризующих второй закон Кирхгофа, значения э. д. с. E и падений напряжений IR считают положительными, если направления э. д. с. и токов на соответствующих участках контура совпадают с произвольно выбранным направлением обхода контура. Если же направления э. д. с. и токов на соответствующих участках контура противоположны выбранному направлению обхода, то такие э. д. с. и падения напряжения считают отрицательными.
Метод контурных токов. При расчете методом контурных токов полагают, что в каждом независимом контуре схемы течет свой контурный ток. Уравнения составляют относительно контурных токов, после чего через них определяют токи ветвей. Таким образом, метод контурных токов можно определить как метод расчета, в котором за искомые принимают контурные токи. Число неизвестных в этом методе равно числу уравнений, которые необходимо было бы составить для схемы по второму закону Кирхгофа. Следовательно, метод контурных токов более экономен при вычислительной работе, чем метод на основе законов Кирхгофа (в нем меньше число уравнений).
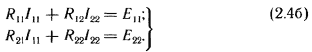
При расчете электрической цепи методом узловых потенциалов определяются потенциалы узлов цепи, а затем по закону Ома токи в ее ветвях. Метод целесообразно применять в тех случаях, когда число узлов цели меньше или равно числу независимых контуров этой цепи. Так, для электрической цепи, имеющей четыре узла, составляется три расчетных уравнения (например, для узлов 1, 2 к 3 потенциал узла 4 принимается равным нулю):
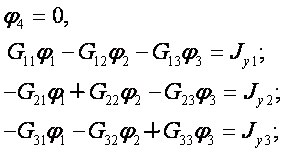
где φk - искомый потенциал K-го узла цепи (K = 1,2, 3) Gkk- (G11, например) собственная (узловая) проводимость k-го узла, равная сумме проводимостей всех ветвей, присоединенных к этому узлу; Gkm -(G12, например) взаимная (межузловая) проводимость узлов k и m, равная суше проводимостей ветвей, включенных непосредственно между этими узлами; Jyk (Jy1, например) - узловой ток к-го узла, определяемый из выражения
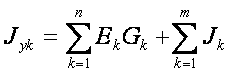
Под знаком первой суммы произведения ЭДС ветвей, присоединенных к К-му узлу, на проводимости этих ветвей учитывается ЭДС с положительным (отрицательным) знаком, если она направлена к К-му узлу (от К-го узла). Под знаком второй суммы со знаком «+» ("-"} учитываются токи источников тока, которые направлены к К-му узлу (от К-го узла). Если в цепи между двумя узлами включен идеальный источник ЭДС (внутреннее сопротивление которого равно нулю), необходимо принимать равным нулю потенциал одного из его зажимов, тогда потенциал другого зажима источника будет равен ЭДС с соответствующим знаком, а количество расчетных уравнений сократится.
Методом двух узлов определяется напряжение между этими узлами, а затем по величине этого напряжения определяются токи ветвей.
Расчетные формулы этого метода получаются на основе выражений (1.9) и (1.10). Рассмотрим метод двух узлов на примере схемы, изображенной на рис. 1.11.
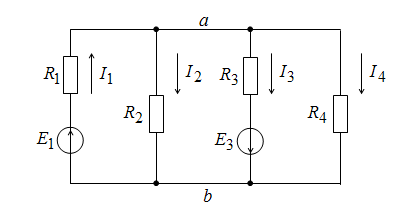
Рис. 1.11. Пример схемы для определения токов методом двух узлов
В формуле (1.10) примем I = 0, тогда
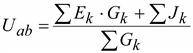 .(1.12)
.(1.12)
Зная Uab, можно определить ток в любой ветви. Так для схемы, изображенной на рис.1.11
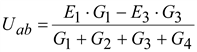 ;
;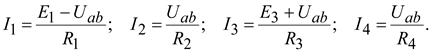
Резистивными называются электрические цепи, в схему замещения которых входят только элементы активного сопротивления и источники.
Электрическая цепь с последовательным соединением элементов
|
|
Последовательным называют такое соединение элементов цепи, при котором во всех включенных в цепь элементах возникает один и тот же ток I (рис. 1.4).
На основании второго закона Кирхгофа (1.5) общее напряжение U всей цепи равно сумме напряжений на отдельных участках:
U=U1+U2+U3 или IRэкв=IR1+IR2+IR3,
откуда следует
(1.5)
Rэкв=R1+R2+R3.
Таким образом, при последовательном соединении элементов цепи общее эквивалентное сопротивление цепи равно арифметической сумме сопротивлений отдельных участков. Следовательно, цепь с любым числом последовательно включенных сопротивлений можно заменить простой цепью с одним эквивалентным сопротивлением Rэкв (рис. 1.5). После этого расчет цепи сводится к определению тока I всей цепи по закону Ома
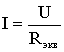 ,
,
и по вышеприведенным формулам рассчитывают падение напряжений U1,U2,U3 на соответствующих участках электрической цепи (рис. 1.4).
Недостаток последовательного включения элементов заключается в том, что при выходе из строя хотя бы одного элемента, прекращается работа всех остальных элементов цепи.
Электрическая цепь с параллельным соединением элементов
Параллельным называют такое соединение, при котором все включенные в цепь потребители электрической энергии, находятся под одним и тем же напряжением (рис. 1.6).
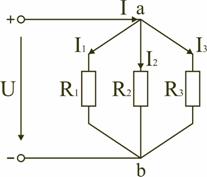
Рис. 1.6
В этом случае они присоединены к двум узлам цепи а и b, и на основании первого закона Кирхгофа (1.3) можно записать, что общий ток I всей цепи равен алгебраической сумме токов отдельных ветвей:
I=I1+I2+I3,
т.е. 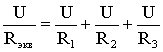 ,
,
откуда следует, что
(1.6)
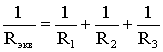 .
.
В том случае, когда параллельно включены два сопротивления R1 и R2, они заменяются одним эквивалентным сопротивлением
(1.7)
![]() .
.
Из соотношения (1.6), следует, что эквивалентная проводимость цепи равна арифметической сумме проводимостей отдельных ветвей:
gэкв=g1+g2+g3.
По мере роста числа параллельно включенных потребителей проводимость цепи gэкввозрастает, и наоборот, общее сопротивление Rэкв уменьшается.
Напряжения в электрической цепи с параллельно соединенными сопротивлениями (рис. 1.6)
U=IRэкв=I1R1=I2R2=I3R3.
Отсюда следует, что
 ,
,
т.е. ток в цепи распределяется между параллельными ветвями обратно пропорционально их сопротивлениям.
По параллельно включенной схеме работают в номинальном режиме потребители любой мощности, рассчитанные на одно и то же напряжение. Причем включение или отключение одного или нескольких потребителей не отражается на работе остальных. Поэтому эта схема является основной схемой подключения потребителей к источнику электрической энергии.
Электрическая цепь со смешанным соединением элементов
Смешанным называется такое соединение, при котором в цепи имеются группы параллельно и последовательно включенных сопротивлений.
Рис. 1.7
Для цепи, представленной на рис. 1.7, расчет эквивалентного сопротивления начинается с конца схемы. Для упрощения расчетов примем, что все сопротивления в этой схеме являются одинаковыми: R1=R2=R3=R4=R5=R. Сопротивления R4 и R5 включены параллельно, тогда сопротивление участка цепи cd равно:
 .
.
В этом случае исходную схему (рис. 1.7) можно представить в следующем виде (рис. 1.8):

Рис. 1.8
На схеме (рис. 1.8) сопротивление R3 и Rcd соединены последовательно, и тогда сопротивление участка цепи ad равно:
![]() .
.
Тогда схему (рис. 1.8) можно представить в сокращенном варианте (рис. 1.9):
Рис. 1.9
На схеме (рис. 1.9) сопротивление R2 и Rad соединены параллельно, тогда сопротивление участка цепи аb равно
 .
.
Схему (рис. 1.9) можно представить в упрощенном варианте (рис. 1.10), где сопротивленияR1 и Rab включены последовательно.
Тогда эквивалентное сопротивление исходной схемы (рис. 1.7) будет равно:
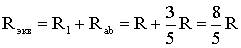 .
.
|
|
В результате преобразований исходная схема (рис. 1.7) представлена в виде схемы (рис. 1.11) с одним сопротивлением Rэкв. Расчет токов и напряжений для всех элементов схемы можно произвести по законам Ома и Кирхгофа.

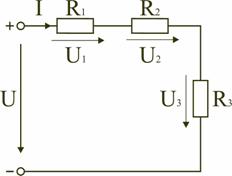 Рис.
1.4
Рис.
1.4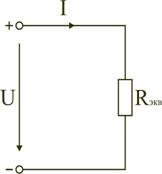 Рис.
1.5
Рис.
1.5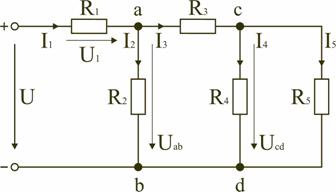
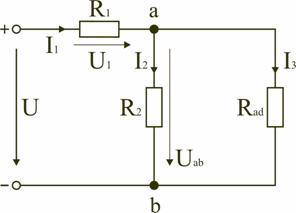
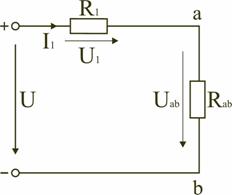 Рис.
1.10
Рис.
1.10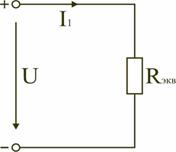 Рис.
1.11
Рис.
1.11