19.Многогранники.Выпуклые и не выпуклые многогранники

Многогранниками  называются тела, поверхности которых состоят из конечного числа многоугольников, назы­ваемых гранями многогранника. Стороны и вершины этих многоугольников называются соответственно ребрами и вершинами многогранника.

Многогранник называется выпуклым, если он является выпуклой фигурой, т.е. вместе с любыми двумя своими точками содержит и соединяющий их отрезок.

Рассмотрим некоторые свойства выпуклых многогранников.

Свойство 1. В выпуклом многограннике все грани являются выпуклыми многоугольниками.

Свойство 2. Выпуклый многогранник может быть составлен из пирамид с общей вершиной, основания которых образуют поверхность многогранника.

Свойство 3. Выпуклый многогранник лежит по одну сторону от плоскости каждой своей грани.

Для выпуклых многогранников имеет место свойство, связывающее число его вершин, ребер и граней, доказанное в 1752 году Леонардом Эйлером, и получившее название теоремы Эйлера.

Невыпуклые

Звёздчатый многогранник (звёздчатое тело) — это невыпуклый многогранник, грани которого пересекаются между собой. Как и у незвёздчатых многогранников, грани попарно соединяются в ребрах, при этом внутренние линии пересечения не считаются рёбрами.Звёздчатой формой многогранника называется многогранник, полученный путём продления граней данного многогранника через рёбра до их следующего пересечения с другими гранями по новым рёбрам.Правильные звёздчатые многогранники — это звёздчатые многогранники, гранями которых являются одинаковые правильные или звёздчатые многоугольники.

20.Призма

Призма — многогранник, две грани которого являются  равными многоугольниками, лежащими в параллельных плоскостях, а остальные грани — параллелограммами, имеющими общие стороны с этими многоугольниками. Или (равносильно) — это многогранник, в основаниях которого лежат равные многоугольники, а боковые грани — параллелограммы.Призма является разновидностью цилиндра.

Элементы призмы 

• Перпендикулярное сечение

• Диагональное сечение

• Полная поверхность

• Боковые ребра

• Высота

• Диагональ

• Диагональная плоскость

• Основания

• Боковые грани

• Боковая поверхность

Свойства призмы:

• Основания призмы являются равными многоугольниками.

• Боковые грани призмы являются параллелограммами.

• Боковые ребра призмы параллельны и равны.

• Объём призмы равен произведению её высоты на площадь основания:

• Площадь полной поверхности призмы равна сумме площади её боковой поверхности и удвоенной площади основания.

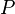• Площадь боковой поверхности произвольной призмы  , где   — периметр перпендикулярного сечения,   — длина бокового ребра.

• Площадь боковой поверхности правильной призмы  , где   — периметр основания призмы, ,   — высота призмы.

• Перпендикулярное сечение перпендикулярно ко всем боковым рёбрам призмы.

• Углы перпендикулярного сечения — это линейные углы двугранных углов при соответствующих боковых рёбрах.

• Перпендикулярное сечение перпендикулярно ко всем боковым граням.

Виды призм:

• Призма, основанием которой является параллелограмм, называется параллелепипедом.

• Прямая призма - это призма, у которой боковые ребра перпендикулярны плоскости основания. Другие призмы называются наклонными.

• Правильная призма - это прямая призма, основанием которой является правильный многоугольник. Боковые грани правильной призмы - равные прямоугольники.

• Правильная призма, боковые грани которой являются квадратами (высота которой равна стороне основания), является полуправильным многогранником.