9.Три правила вычисления первообразных

Существует три основных правила нахождения первообразных функций. Они очень похожи на соответствующие правила дифференцирования.

Правило 1

Если F есть первообразная дл некоторой функции f, а G есть первообразная для некоторой функции g, то F + G будет являться первообразной для f + g.

По определению первообразной F’ = f. G’ = g. А так как эти условия выполняются, то по правилу вычисления производной для суммы функций будем иметь: 

(F + G)’ = F’ + G’ = f + g.

Правило 2

Если F есть первообразная для некоторой функции f, а k – некоторая постоянная. Тогда k*F есть первообразная для функции k*f. Это правило следует из правила вычисления производной сложной функции.

Имеем: (k*F)’ = k*F’ = k*f.

Правило 3

Если F(x) есть некоторая первообразная для функции f(x), а k и b есть некоторые постоянные, причем k не равняется нулю, тогда (1/k)*F*(k*x+b) будет первообразной для функции f(k*x+b).

Данное правило следует из правила вычисления производной сложной функции:

((1/k)*F*(k*x+b))’ = (1/k)*F’(k*x+b)*k = f(k*x+b).

10 . Неопределенный интеграл. Геометрический смысл неопределенного интеграла.

11.Определенный интеграл. Формула Ньютона-Лейбница.

Формула Ньютона — Лейбница или основная теорема анализа даёт соотношение между двумя операциями: взятием определённого интеграла и вычислением первообразной.

Если 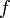  непрерывна на отрезке   и   — её любая первообразная на этом отрезке, то имеет место равенство

Определённый интеграл — аддитивный монотонный нормированный функционал, заданный на множестве пар, первая компонента которых есть интегрируемая функция или функционал, а вторая — область в множестве задания этой функции (функционала).

Определение:

Пусть   определена на  . Разобьём  на части с несколькими произвольными точками  . Тогда говорят, что произведено разбиение   отрезка   Далее выберем произвольную точку ,  ,

Определённым интегралом от функции   на отрезке  называется предел интегральных сумм при стремлении ранга разбиения к нулю  , если он существует независимо от разбиения   и выбора точек  , то есть

Если существует указанный предел, то функция   называется интегрируемой на   по Риману.

Обозначение:

•  — нижний предел.

•  — верхний предел.

•  — подынтегральная функция.

•  — длина частичного отрезка.

•  — интегральная сумма от функции   на   соответствующей разбиению  .

•  — максимальная длина част. отрезка.

Свойства:

Если функция   интегрируема по Риману на  , то она ограничена на нем.

12.Аксиомы стереометрии

 А к с и о м а 1.Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.

 А к с и о м а 2.Если две точки прямой лежат в плоскости, то все точки данной прямой лежат в этой плоскости.В этом случае говорят, что прямая лежит в плоскости или что плоскость проходит через прямую.Из аксиомы 2 следует, что прямая, не лежащая в плоскости, не может иметь с плоскостью более одной общей точки. Если прямая и плоскость имеют только одну общую точку, то говорят, что прямая пересекает плоскость.

 А к с и о м а 3.Если две плоскости имеют общую точку, то они имеют общую прямую, которой принадлежат все общие точки этих плоскостей.В этом случае говорят, что плоскости пересекаются по прямой.

 А к с и о м а 4.В любой плоскости пространства выполняются все аксиомы планиметрии.Таким образом, в любой плоскости пространства можно использовать все доказанные теоремы и формулы из планиметрии.