2. Потенциал и разность потенциалов. Эквипотенциальные поверхности. Связь между напряженностью и разностью потенциалов.

Потенциальная энергия заряда в электростатическом поле пропорциональна самому заряду. Это справедливо как для однородного, так и для любого другого. В частности, потенциальная энергия заряда q2 в поле точечного заряда q1 пропорциональна заряду q2. Следовательно, отношение потенциальной энергии к заряду не зависит от помещенного в поле заряда. Это позволяет ввести новую количественную характеристику электростатического поля - потенциал, не зависящую от помещенного в поле заряда. Потенциалом электростатического поля называют отношение потенциальной энергии заряда в поле к этому заряду. ϕ =

Т.к. потенциальная энергия Wp = qϕ, то работа равна:

A = - (Wp2 - Wp1) = -q(ϕ1 - ϕ2) = -qΔϕ

Тогда получаем : ϕ2 - ϕ1 = Δ ϕ - это разность потенциалов.

Под разностью потенциалов (обозначается буквой U) понимают разность значений потенциала в начальной и конечной точках траектории. U = ϕ1 - ϕ2 = -Δ ϕ =

Разность потенциалов (напряжение) межу двумя точками равна отношению работы поля при перемещении заряда из начальной точки в конечную к этому заряду. Разность потенциалов между двумя точками равна единице, если при перемещении заряда в 1 Кл из одной точки поля в другую электрическое поле совершает работу в 1 Дж.

При перемещении заряда под углом 90˚ к линиям напряженности электрическое поле не совершает работы, так как сила перпендикулярна перемещению. Значит, если провести поверхность, перпендикулярную в каждой точке линиям напряженности, то при перемещении заряда вдоль этой поверхности работа не совершается. А это, в свою очередь, означает, что все точки поверхности, перпендикулярной линиям напряженности, имеют один и тот же потенциал. Поверхности равного потенциала называют эквипотенциальными. Эквипотенциальной является поверхность любого проводника в электростатическом поле. Ведь силовые линии перпендикулярны поверхностям проводника. Причем не только поверхность, но и все точки внутри проводника имеют один и тот же потенциал. Напряженность поля внутри проводника равна нулю, значит, равна нулю и разность потенциалов между любыми точками проводника.

Потенциал имеет ряд преимуществ.

1. Напряженность поля E - вектор, значение которого определяется полностью 3 независимыми величинами - проекциями вектора на координатные оси. Потенциал - скаляр. Для задания его нужна только одна величина.

2. Подобно тому как опасность со стороны падающего камня непосредственно определяется не силой тяжести, а совершенной полем силы тяжести работой, многие процессы определяются не напряженностью электрического поля в данном месте, а разностью потенциалов.

3. Разность потенциалов гораздо легче измерить, чем напряженность поля. Для определения напряженности поля нужно измерить силу, действующую на заряженный шарик. Для этого следует закрепить на пружинках и фиксировать деформацию пружинок при действии поля на заряд. Для измерения разности потенциалов ничего подобного не нужно.

______________________________________________________________________________________________________

Билет № 4.

1. Работа в термодинамике. Расчет работы по графикам процессов. Первый закон термодинамики.

2. Диэлектрики в электростатическом поле. Поляризация диэлектриков. Диэлектрическая проницаемость.

3. Задача на уравнение Менделеева-Клапейрона.

4. Задача на капиллярные явления.

______________________________________________________________________________________________________

1. Работа в термодинамике. Расчет работы по графикам процессов. Первый закон термодинамики.

В термодинамике движение тела как целого не рассматривается и речь идет о перемещении частей макроскопического тела друг относительно друга. При совершении работы меняется объем тела, а его скорость остается равной нулю. Но скорости молекул тела, например газа, меняется. Поэтому и меняется и температура тела. Итак, при совершении работы в термодинамике меняется состояние макроскопических тел: меняется объем и температура. Вычислим работу в зависимости от изменения объема на примере газа в цилиндре под поршнем. Проще всего вначале вычислить не работу силы F, действующей на газ со стороны внешнего тела (поршня), а работу, которую совершает сам газ, действуя на поршень с силой F'. Согласно третьему закону Ньютона: F = -F'. Модуль силы, действующей со стороны газа на поршень, равен F' = pS, где p - давление газа, S - площадь поверхности поршня. Пясть газ расширяется и поршень смещается в направлении силы на малое расстояние Δh = h2 - h1. Если перемещение мало, то давление газа можно считать постоянным. Работа газа равна:

A' = F'Δh = pS(h2 - h1) = p(Sh1 - Sh2)

Эту работу можно выразить через изменение работы газа. Начальный объем V1 = Sh1, а конечный V2= Sh2. Потому

A' = p(V2 - V1) = pΔV, где ΔV = V2 - V1 - изменение объема газа.

При расширении газ совершает положительную работу, так как направление силы и перемещения совпадают. Работа A, совершаемая внешними телами над газом, отличается от работы газа A' только знаком: A = A', так как сила F, действующая на газ, направлена против силы F', а перемещение остается тем же самым. Поэтому работа внешних сил, действующих на газ, равна:

A= -A' = -pΔV

Знак минус указывает, что при сжатии газа, когда ΔV = V2 - V1 < 0, работа внешней силы положительна. Понятно, почему в этом случаи A > 0: при сжатии газа направления силы и перемещения совпадают. При расширении газа, наоборот, работа внешних сил отрицательна (A < 0), так как

ΔV = V2 - V1 < 0, теперь направления силы и перемещения противоположны.

Работа газа A' для случая постоянного давления можно дать простое геометрическое истолкование. Построим график зависимости давления газа от объема. Здесь площадь прямоугольника ABCD, ограниченная графиком pBC = const, осью V и отрезками AB и CD, равными давлению газа, численно равна работе.

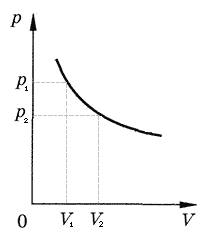
В общем случае при произвольном изменении объема газа давление не остается неизменным. Например, при изотермическом процессе оно убывает обратно пропорционально объему. В этом случае для вычисления работы нужно общее изменение объема разделить на малые части, вычислить элементарные (малые) работы, а потом все их сложить. Работа газа по-прежнему будет численно равна площади фигуры, ограниченной графиком зависимости p от V, осью V и отрезками V1 и V2, равными делениями p1 и p2 в начальном и конечном состояниях.

Изменение полной энергии (механической E и внутренней U) при переходе системы из начального состояния 1 в конечное 2 равно сумме работы внешних сил и количества теплоты, переданного системе:

(E2 + U2) - (E1 + U1) = A + Q

В теории тепловых явлений обычно рассматривают тела, положение центра масс которых изменяется незначительно. В этом случае механическая энергия практически не меняется: E1 = E2. Считая механическую энергию неизменной, мы можем первый закон термодинамики сформулировать следующим образом:

Изменение внутренней энергии системы при переходе ее из одного состояния в другое равно сумме работы внешних сил и количества теплоты, переданного системе, и не зависит от способа, которым осуществляется этот переход.

ΔU = A + Q

Часто вместо работы A внешних тел над системой рассматривают работу A' системы над внешними телами. Учитывая, что A' = -A, первый закон термодинамики можно переписать так:

Q = ΔU + A'

Количество теплоты переданное системе, идет на изменение ее внутренней энергии и на совершение системой работы над внешними телами.