2.3 Задача про вибірку

У партії з 10 деталей, 6 стандартні. Контролер взяв навмання 4 деталі. Обчислити ймовірність того, що хоча б одна з узятих деталей буде стандартною.

Розв’язання

Елементарним наслідком є вибір будь-яких деталей із загального числа 10. Число всіх таких наслідків дорівнює числу комбінацій з 10 по 4, тобто .

Подія А – із 4 деталей, одна бракована.

Наслідком , який сприяє появі події А, є поява групи з 4 деталей, в якій одна стандартна. Групу бракованих деталей можна знайти: 10 – 6 = 4 (брак), тобто , а групу стандартних деталей , так як ці події виконуються одночасно, то наслідки які сприяють появі події А дорівнюють .

Тоді

2.5 В ящику 12 деталей, з яких 8 стандартних. Робітник бере навмання дві деталі. Обчислити ймовірність того , дві деталі будуть стандартні.

Розв’язання

Подія А – перша взята деталь стандартна.

В – друга взята деталь стандартна.

Ймовірність того, що обидві деталі будуть стандартними, знаходимо за теоремою множення ймовірностей залежних подій.

2.6 Ймовірність влучень в ціль з одного пострілу становить 0,8. Знайти ймовірність семи влучень при 10 пострілах.

Розв’язання

За формулою Бернуллі:

n = 10, k = 7, p = 0,8, q = 1 – 0,8 =0,2

2.7 На складі надійшли деталі з трьох верстатів. На першому верстаті виготовлено 40% деталей загальної кількості, на другому - 35%, на третьому - 25%, причому на першому було виготовлено 90% деталей першого сорту, на другому - 80% і на третьому - 70%. Яка ймовірність того, що взята навмання деталь буде першого сорту?

Розв’язання

Позначимо події

Н₁ - деталь виготовлена на першому верстаті,

Н₂ – на другому , Н₃ - на третьому.

Подія А - деталь першого сорту.

Ймовірність - деталь першого сорту

Тобто за формулою повної ймовірності:

2.8 Знайти ймовірність того, що подія А відбудеться рівно 70 раз в 243 іспитах, якщо ймовірність появи цієї події в кожному іспиті = 0,25.

Розв’язання:

За умовою, n =243, k = 70, р = 0,254 ; q=0,75. Так як n=243 – достатньо велике число, скористуємося локальною теоремою Лапласа.

φ(х),

див. Додаток 1, φ(1,37)=0,1561

маємо: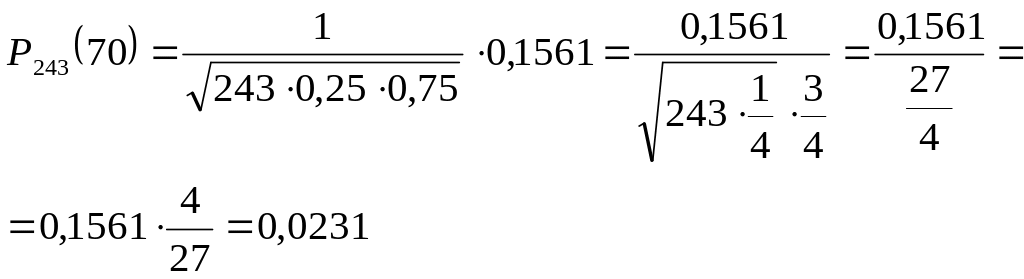

Відповідь: 0,0231

2.9 Ймовірність появи події в кожному із 100 незалежних іспитів дорівнює 0,8. Знайти ймовірність того, що подія відбувається не менше 75 разів і не більше 90 разів.

Розв’язання : за інтегральною теоремою Лапласа

,

; ,

за умовою: n = 100 ; p =0.8; q = 0.2; ;

див. Додаток 2. Ф (-1,25) = -Ф(1,25)= - 0,3944

Ф(2,5) = 0,4938

Маємо Р (75;90) = 0,4938+0,3944 = 0,8882

Відповідь: 0,8882

3 Запитання для самоконтролю

3.1 Дати означення ймовірності.

3.2 Назвіть, які події називаються несумісними і сумісними.

3.3 Визначте, що називається сумою двох подій та добутком.

3.4 Запишіть формулу повної ймовірності та формулу Байєса.

3.5 Запишіть формулу Бернуллі.

3.6 Запишіть локальну та інтегральну теореми Лапласа.