Інтервальний варіаційний ряд

Для побудови інтервального варіаційного ряду діапазон значень ознак , який називається розмахом варіації, ділимо на k – інтервалів. Підраховуємо m_i (i = 1,2,. . . к), яке відноситься до відповідного інтервалу і показує, скільки варіант потрапляють у даний i-тий інтервал. - розмах варіації.

Кількість інтервалів k, розмах варіації R та довжина інтервалу h пов’язані між собою співвідношенням: R = К · h.

довжина інтервалу: h =

Кількість інтервалів, на які розбивається уся сукупність, залежить від об’єму сукупності.

Існує декілька способів знаходження кількості класів, але на практиці можна користуватися таблицею:

Таблиця №1 Кількість класів

Кількість варіант	Кількість класів, k
25 – 40	5 – 6
40 – 60	6 – 8
60 – 100	7 – 10
100 – 200	8 – 12
200 - . . .	10 – 15

Таким чином, інтервальний ряд становить з себе ряд напіввідчинених інтервалів:

де 1.2.6

.

Звичайно варіаційний інтервальний ряд задається таблицею:

Таблиця №2 Варіаційний інтервальний ряд

Номер інтервалу	Границі інтервалів:	Частота ni	Щільність
1		n1
2		n2
3		n3
. . .	. . .	. . .	. . .
n		nn

Гістограма частот – це ступенева фігура, що складається з прямокутників, основа яких – довжина інтервалу (крок інтервалу), а висота дорівнює m_i .

Малюнок 1 Гістограма частот

Полігон розподілу будується так само, як у звичайного варіаційного ряду, де - середини інтервалів.

1.3 Числові характеристики

1.3.1 Середнє арифметичне:

, 1.3.1

де - середини інтервалів;

2. Дисперсія

, або 1.3.2

Виправлена дисперсія 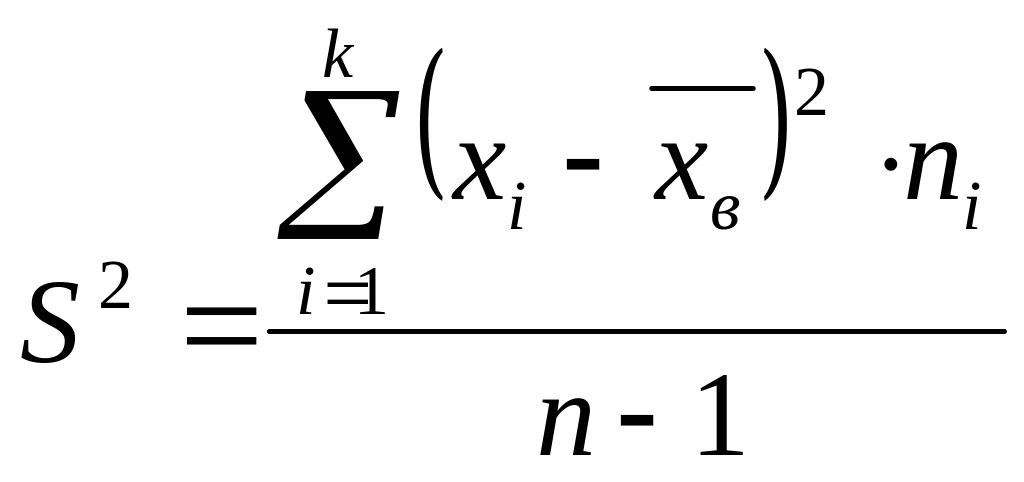, 1.3.3

де - середини інтервалів, використовується в оцінюванні генеральної дисперсії

1.4 Статистичні оцінки.

1.4.1 Вибіркове середнє

, 1.4.1

1.4.2 Вибіркова дисперсія

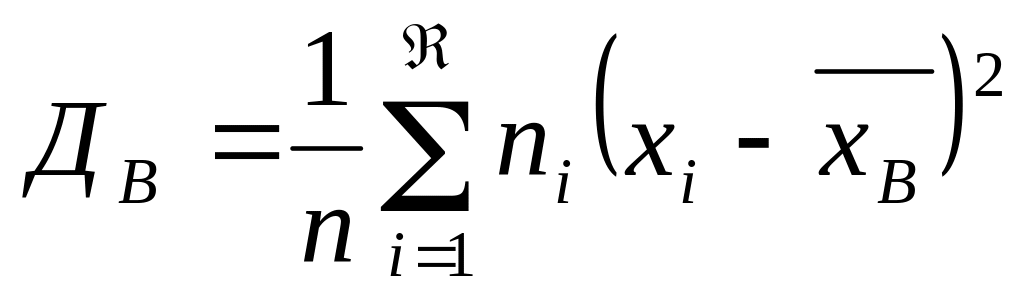, або , 1.4.2

1.4.3 Середнє квадратичне відхилення

, 1.4.3

1.4.4 Виправлена вибіркова дисперсія (для великих n)

1.4.4