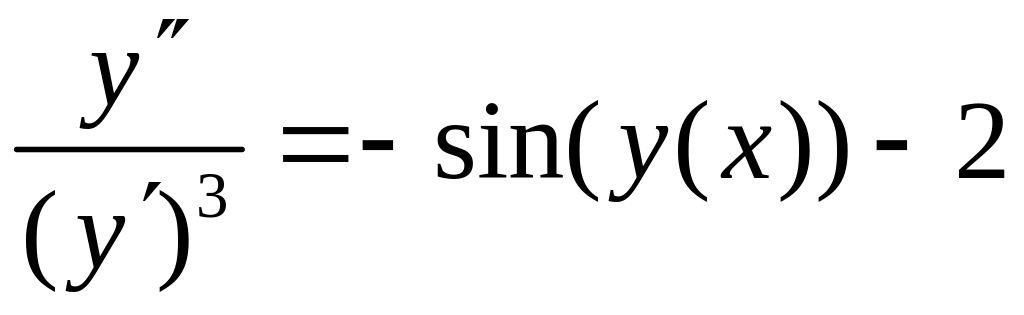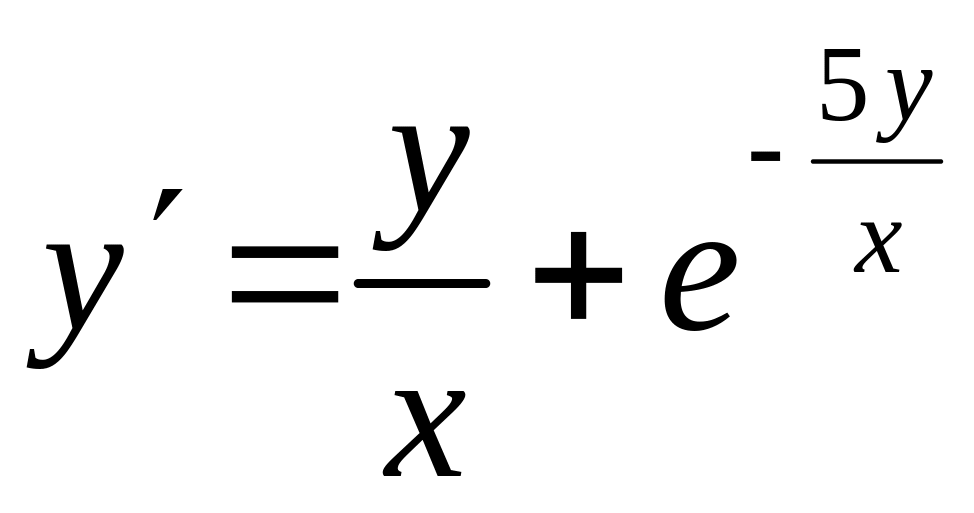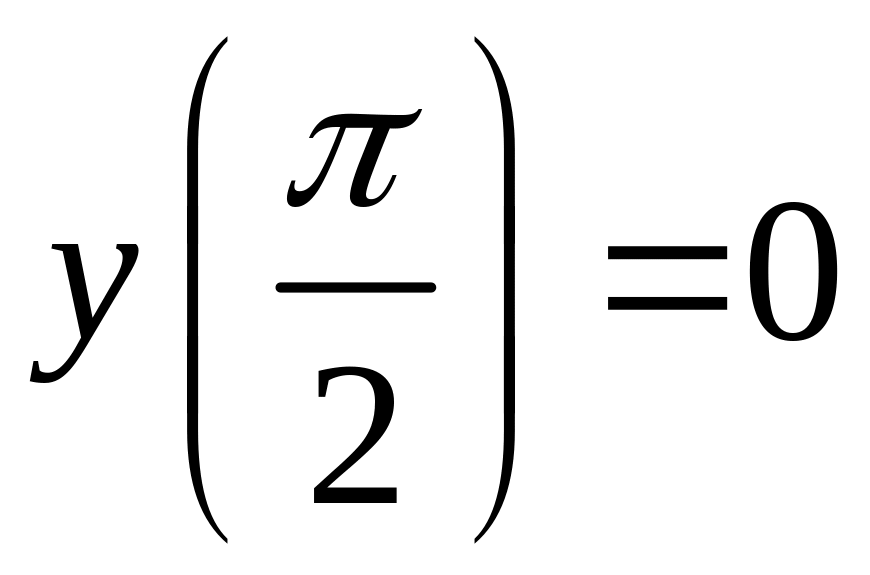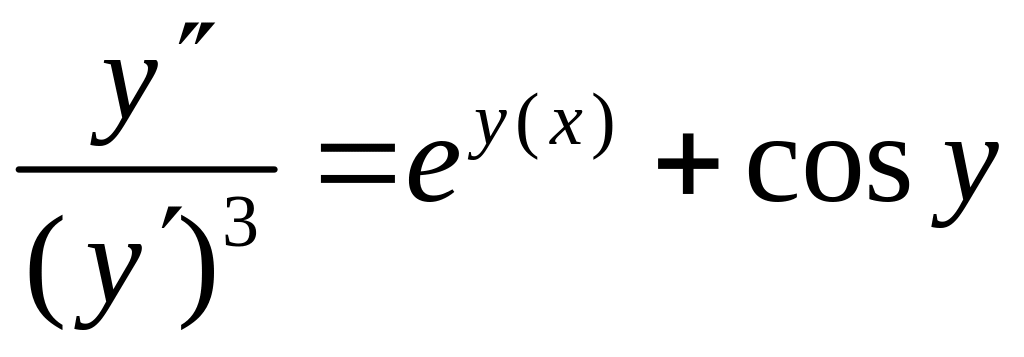- •Экономики и торговли
- •Донецк 2007
- •Введение
- •Обыкновенные дифференциальные уравнения
- •1.1. Общие понятия
- •1.2. Математические модели некоторых экономических
- •1.3. Тестовые контрольные вопросы к разделу 1
- •1.4. Контрольные задания для самостоятельного решения к разделу 1
- •Дифференциальные уравнения первого порядка
- •2.1. Дифференциальные уравнения с разделяющимися
- •2.2. Однородные дифференциальные уравнения первого
- •2.3. Линейные дифференциальные уравнения первого
- •Подставим равенства (2.3.2) и (2.3.3) в заданное уравнение (2.3.1), тогда оно примет вид или
- •Пример 2.3.4. Найти общее решение дифференциального уравнения .
- •2.4. Тестовые контрольные вопросы к разделу 2
- •3. Общее решение дифференциального уравнения первого порядка с геометрическое точки зрения это
- •2.5. Контрольные задания для самостоятельного решения к разделу 2
- •Дифференциальные уравнения второго порядка
- •3.1. Дифференциальные уравнения второго порядка,
- •3.2. Линейные однородные дифференциальные уравнения с
- •3.3. Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами второго порядка
- •Алгоритм нахождения решения методом Лагранжа
- •3.4. Тестовые контрольные вопросы к разделу 3
- •3. Общее решение дифференциального уравнения второго порядка с геометрическое точки зрения это
- •3.5. Контрольные задания для самостоятельного решения к разделу 3
- •4. Ответы на контрольные задания для самостоятельного решения
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
- •Предметный указатель
- •Литература
- •Содержание
Вариант 8
Найти общее решение или общий интеграл дифференциального уравнения первого порядка
1) |
|
а)
|
б)
|
||
в)
|
||
г)
|
||
д) другой ответ |
||
2) |
|
а) |
б) |
||
в) |
||
г) |
||
д) другой ответ |
||
3) |
|
а) |
б) |
||
в) |
||
г)
|
||
д) другой ответ |
||
4) |
|
а)
|
б)
|
||
в)
|
||
г)
|
||
д) другой ответ |
Найти частное решение дифференциального уравнения, удовлетворяющее начальному условию (решение задачи Коши)
5) |
|
а)
|
б)
|
||
в)
|
||
г)
|
||
д) другой ответ |
||
6) |
, |
а)
|
б)
|
||
в)
|
||
г)
|
||
д) другой ответ |
Найти общее решение линейного дифференциального уравнения второго порядка
7) |
|
а)
|
б)
|
||
в)
|
||
г)
|
||
д) другой ответ |
||
8) |
|
а)
|
б)
|
||
в)
|
||
г) |
||
д) другой ответ |
Найти общее решение дифференциального уравнения второго порядка, допускающего понижение порядка
9) |
|
а)
|
б)
|
||
в)
|
||
г)
|
||
д) другой ответ |
||
10) |
|
а)
|
б)
|
||
в)
|
||
г)
|
||
д) другой ответ |
Вариант 9
Найти общее решение или общий интеграл дифференциального уравнения первого порядка
1) |
|
а)
|
б)
|
||
в)
|
||
г)
|
||
д) другой ответ |
||
2) |
|
а)
|
б)
|
||
в)
|
||
г)
|
||
д) другой ответ |
||
3) |
|
а)
|
б)
|
||
в) |
||
г)
|
||
д) другой ответ |
||
4) |
|
а)
|
б)
|
||
в)
|
||
г)
|
||
д) другой ответ |
Найти частное решение дифференциального уравнения, удовлетворяющее начальному условию (решение задачи Коши)
5) |
|
а)
|
б)
|
||
в)
|
||
г)
|
||
д) другой ответ |
6) |
|
а)
|
б)
|
||
в)
|
||
г)
|
||
д) другой ответ |
Найти общее решение линейного дифференциального уравнения второго порядка
7) |
|
а) |
б)
|
||
в)
|
||
г)
|
||
д) другой ответ |
||
8) |
|
а)
|
б)
|
||
в)
|
||
г)
|
||
д) другой ответ |
Найти общее решение дифференциального уравнения второго порядка, допускающего понижение порядка
9) |
|
а) |
б)
|
||
в)
|
||
г)
|
||
д) другой ответ |
||
10) |
|
а)
|
б)
|
||
в)
|
||
г)
|
||
д) другой ответ |