3.3. Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами второго порядка

!	Уравнение называется линейным неоднородным дифференциальным уравнением с постоянными коэффициентами второго порядка, если оно имеет вид , (3.3.1) где p и q – постоянные числа, – функция переменной х.

В общем случае линейное неоднородные дифференциальное уравнение с постоянными коэффициентами второго порядка (3.3.1) может быть решено методом вариации произвольных постоянных (методом Лагранжа).

Алгоритм нахождения решения методом Лагранжа

1. Найти общее решение однородного линейного дифференциального уравнения (3.2.1), соответствующего исходному неоднородному линейному дифференциальному уравнению (3.3.1) , где , .

2. Предполагая, произвольные постоянные и являются функциями независимой переменной x, т.е. и , следует искать общее решение неоднородного уравнения (3.3.1) в виде общего решения однородного уравнения , при этом функции и могут быть найдены из решения системы

(3.3.2)

Пример 3.3.1. Найти общее решение дифференциального уравнения с помощью метода вариации произвольных постоянных.

Решение. Это обыкновенное линейное неоднородное дифференциальное уравнением второго порядка с постоянными коэффициентами.

Найдем общее решение соответствующего однородного дифференциального уравнения, т.е. уравнения . Характеристическое уравнение этого линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами таково: . Его корни k₁ = - 1, k₂ = 4, поэтому общее решение рассматриваемого однородного дифференциального уравнения, найденное по формуле (3.2.3), таково

. (3.3.3)

Будем искать общее решение линейного неоднородного дифференциального уравнения в виде общего решения однородного линейного уравнения (3.3.3), считая, что произвольные постоянные являются функциями независимой переменной x, т.е. в виде

. (3.3.4)

Функции и  могут быть найдены из решения системы (3.3.2) с учетом решения (3.3.3), поскольку , , , тогда , т.е.

Поскольку , то , откуда функция .

Поскольку , то , т.е.

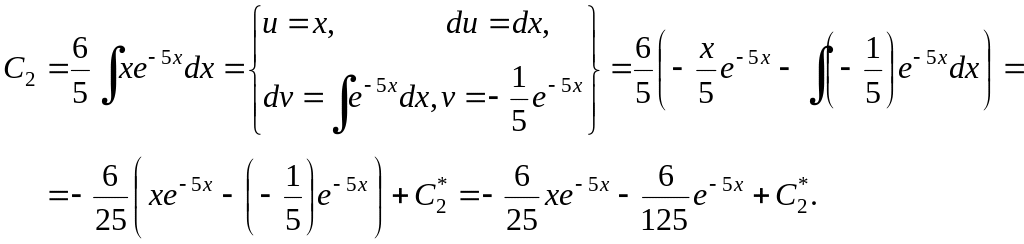
Откуда функция

Подставим найденные функции и  в формулу (3.3.4), тогда

или

.

Обозначив через , , окончательно получим общее решение неоднородного дифференциального линейного уравнения

.

Метод вариации произвольных постоянных достаточно сложен, поэтому в ряде случаев, когда правая часть линейного неоднородного дифференциального уравнения с постоянными коэффициентами второго порядка имеет специальный вид, можно использовать другой метод – метод неопределенных коэффициентов.

Для этого следует воспользоваться утверждением о структуре общего решения неоднородного обыкновенного дифференциального уравнения.

Теорема 3.3.1. Общее решение линейного неоднородного дифференциального уравнения с постоянными коэффициентами второго порядка (3.3.1) равно сумме общего решения соответствующего линейного однородного дифференциального уравнения (3.2.1) и частного решения линейного неоднородного дифференциального уравнения (3.3.1):

= + , (3.3.4)

где – общее решение линейного неоднородного дифференциального уравнения (3.2.1), – общее решение линейного однородного дифференциального уравнения (3.2.2), – частное решение линейного неоднородного дифференциального уравнения (3.2.1).

Частное решение линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами (3.3.1) ищут с помощью метода неопределенных коэффициентов по виду правой части.

Если правая часть линейного неоднородного дифференциального уравнения с постоянными коэффициентами второго порядка (3.3.1) имеет вид

, (3.3.4)

где  – многочлены степени n и m соответственно, а и b – некоторые постоянные числа, то частное решение неоднородного уравнения будет иметь следующую структуру:

, (3.3.5)

где  – многочлены степени , записанные с помощью неопределенных коэффициентов; – равно числу корней характеристического уравнения (3.2.2), совпадающих с числом .

Замечание 3.3.1. Таким образом, = 0, если среди корней характеристического уравнения (3.2.2)  нет числа , т.е. ; = 1, если существует один корень характеристического уравнения (3.2.2)  или , совпадающий с числом , т.е. ; = 2, если существует двукратный корень характеристического уравнения (3.2.2), совпадающий с числом , т.е. .

Зная структуру частного решения (3.3.5) линейного неоднородного дифференциального уравнения, неизвестными которого являются только коэффициенты многочленов, его следует подставить вместе с производными в исходное дифференциальное уравнение (3.3.1) и, приравнивая коэффициенты подобных членов слева и справа, получить необходимое количество линейных алгебраических уравнений для вычисления этих неизвестных коэффициентов.

Таким образом, для линейного неоднородного дифференциального уравнения с правой частью специального вида общее решение может быть найдено с помощью элементарных операций, таких как дифференцирование и решение линейных алгебраических уравнений, не прибегая к операции интегрирования, которая необходима в методе вариации произвольных постоянных.

Пример 3.3.2. Найти общее решение дифференциального уравнения с помощью метода неопределенных коэффициентов.

Решение. Из примера 3.3.1 известно, что общее решение однородного дифференциального уравнения соответствующего данному неоднородному уравнению имеет вид (3.3.3), т.е. .

Для нахождения частного решения исходного линейного неоднородного дифференциального уравнения второго порядка рассмотрим его правую часть, которая имеет специальный вид . С учетом формулы (3.3.4) имеем

. (3.3.6)

Формула (3.3.6) будет верна, если , т.е. , , т.е. т = 0. Так как правая часть исходного дифференциального уравнения имеет специальный вид, то структура частного решения может быть определена по формуле (3.3.5).

Так как  и число , то = 1. Так как  и т =0, то , т.е. , . Тогда частное решение исходного неоднородного дифференциального уравнения с неопределенными коэффициентами будет иметь следующую структуру: или

. (3.3.7)

Для нахождения коэффициентов A и B методом неопределенных коэффициентов решение (3.3.7) следует подставить в исходное неоднородное дифференциальное уравнение.

Для этого найдем первую и вторую производные от частного решения (3.3.7):

, откуда

, (3.3.8)

, откуда

. (3.3.9)

Подставим решение (3.3.7), найденные выражения (3.3.8), (3.3.9) в исходное дифференциальное уравнение:

Разделим обе части полученного равенства на , поскольку :

или после преобразований: .

Поскольку из алгебры известно, что два многочлена равны тогда и только тогда, когда равны коэффициенты при соответствующих степенях, приравняв коэффициенты при одинаковых степенях переменной, получим систему, из которой найдем коэффициенты А  и В:

Решая эту систему двух линейных алгебраических уравнений с двумя переменными, получим , . Подставляя полученные значения коэффициентов А и В в формулу (3.3.7), найдем частное решение в виде:

или .

Тогда по формуле (3.3.4) общее решение исходного линейного неоднородного дифференциального уравнения второго порядка имеет вид

.

Замечание 3.3.2. Сравнивая общее решение дифференциального уравнения, полученное методом вариации произвольных постоянных и методом замены переменных – они совпадают, - обратим внимание на структуру полученного решения: первые два слагаемых – это общее решение однородного дифференциального уравнения, последнее – частное решение неоднородного дифференциального уравнения.

Пример 3.3.3. Найти общее решение неоднородного дифференциального уравнения .

Решение. Для однородного дифференциального уравнения, которое соответствует данному неоднородному дифференциальному уравнению второго порядка с постоянными коэффициентами, характеристическое уравнение таково . Его корни , – действительные и различные. Поэтому общее решение рассматриваемого однородного дифференциального уравнения по формуле (3.2.5) имеет вид

. (3.3.10)

По виду правой части исходного неоднородного дифференциального уравнения с учетом формулы (3.3.4) имеем

. (3.3.11)

Формула (3.3.11) будет верна, если , т.е. , , т.е. т = 0. Так как правая часть исходного дифференциального уравнения имеет специальный вид, то структура частного решения может быть определена по формуле (3.3.5).

Так как  и число , то = 0. Так как  и т =0, то , т.е. , . Тогда частное решение исходного неоднородного дифференциального уравнения с неопределенными коэффициентами будет иметь следующую структуру: или

. (3.3.12)

Для нахождения неопределенных коэффициентов А и В подставим решение (3.3.12) в исходное линейное неоднородное дифференциальное уравнение, помня, что , .

Получим или . Поскольку из алгебры известно, что два многочлена равны тогда и только тогда, когда коэффициенты при соответствующих степенях равны, то получим систему уравнений для нахождения неопределенных коэффициентов А и В

(3.3.13)

Решив систему (3.3.13), найдем , . Подставив эти значения в формулу (3.3.12), найдем частное решение неоднородного дифференциального уравнения

. (3.3.14)

Общее решение рассматриваемого линейного неоднородного дифференциального уравнения второго порядка по формуле (3.2.4) равно сумме решений, записанных формулами (3.3.10) и (3.3.14), т.е. оно имеет вид

.