
- •Системы счисления. Позиционные и непозиционные.
- •Основные логические схемы.
- •Основные операции булевой алгебры.
- •Законы булевой алгебры.
- •Комбинационные логические схемы
- •Цифровые интегральные схемы Виды логических схем
- •Триггеры
- •Типы триггеров
- •Регистры
- •Выходные буферные схемы.
- •Счетчики
- •Сумматоры
- •Дешифраторы
- •Мультиплексоры
- •Элементы памяти
- •Параметры и характеристики цап и ацп.
- •Классификация ацп.
- •Классификация цап.
- •Классификация и основные определения микропроцессорных средств.
Системы счисления. Позиционные и непозиционные.
Любая цифровая система работает в двоичной системе счисления.
1 разряд называется битом
8бит=1байт, 1024бита=1Кбайт
Двоичная система - позиционная система, то есть каждой позиции (разряду) присвоен определенный вес.
20=1, 21=2, 22=4...
Для сокращения используют восьмеричную и шестнадцатиричную системы
4510=558=2D16
Основные логические схемы.
Логической схемой называют такую схему, которая выполняет логические операции над одной или более логическими переменными.
Логическая переменная – это электрический сигнал, принимающий 2 различных значения, которые можно условно назвать нулем и единицей (ист., лож.).
Раздел математики, где описаны свойства величин, принимающих только 2 значения, называется булевой алгеброй.
Булевая алгебра содержит переменные 1 и 0.
Основные операции булевой алгебры.
1. Операция отрицания (инверсия), «не»
![]() ,
,![]()
2. Операция умножения, «и»
Х1٨ Х2
0*0=0, 0*1=0, 1*0=0, 1*1=1
3. Сложение, «или»
Х1٧Х2
0+0=0, 0+1=1, 1+0=1, 1+1=1
Y=Х1![]() 2+
1Х2=
Х1(+)Х2
– исключающее «или»
2+
1Х2=
Х1(+)Х2
– исключающее «или»
Законы булевой алгебры.
В двоичной системе действует дуальный (двойственный) закон, согласно которому операции умножения и сложения допускают взаимную замену с одновременной заменой всех 1 на 0 и наоборот.
1. Переместительный закон
Х1*Х2= Х2*Х1
Х1+Х2= Х2+Х1
2. Сочетательный закон
Х1*( Х2*Х3)= Х3*( 2*Х1)=Х2*(Х3*Х1)
Х1+( Х2+Х3)= Х3+(Х2+ 1)=Х2+(Х3+Х1)
3. Закон повторения (тавтологии)
Х+Х=Х
Х*Х=Х
4. Закон обращения
Х1= Х2 → 1= 2
5. Двойная инверсия
![]() =Х
=Х
6. Закон нулевого множества
Х*0=0
Х+0=Х
7. Закон универсального множества
Х*1=1
Х+1=1
8. Закон дополнительности
Х* =0
Х+ =1
9. Распределительный закон
Х1*(Х2+Х3)=Х1*Х2+Х1*Х3
Х1+Х2*Х3=(Х1+Х2)*(Х1+Х3)
10. Закон поглощения
Х1+(Х1*Х1)=Х1
Х1*(Х1+Х1)=Х1
11. Закон склеивания
(Х1+ Х2)*( Х1+ 2)= Х1
Х1* Х2+ Х1* 2= Х1
12. Закон инверсии ДеМоргана
![]()
Х1*Х2=![]()
Х1+Х2=![]()
Комбинационные логические схемы
и-не

или-не
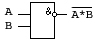
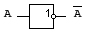
не
исключающее или А
 В
В
Цифровые интегральные схемы Виды логических схем
1. Транзисторно-транзисторная логика(ТТЛ)
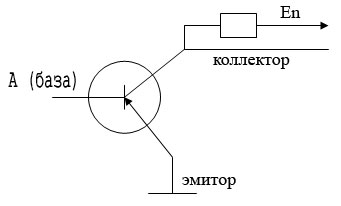
Напряжение Еn
больше или меньше 0 для p-n-p
или n-p-n
транзисторов соответственно, этом
сигнал логической переменной А, подаваемый
на входе преобразуется на выходе в
![]() ,
т.о. реализуется операция инвертирования.
,
т.о. реализуется операция инвертирования.
Полевой транзистор

МОП-транзистор
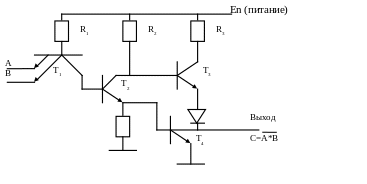
Стандартная ТТЛ-схема выполняет операцию И-НЕ
Серия 155, в 70-х гг протеблял мощность 12мВТ/элемент, задержка составляла 10нс/элемент
Серия 1533, конец 80-х гг, потребляемая мощность 2мВт/элемент, задержка 4нс/элемент
Диодно-транзисторная логика

Потребляемая мощность 8мВт/элемент, задержка 30нс/элемент.
Логика МОП
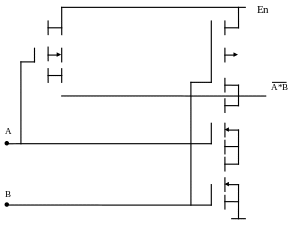
П реимущества:
входное сопротивление порядка 1012
Ом, т.е ток входной цепью фактически не
потребляется; потребляемая мощность
связанна лишь с утечкой в полевом
моп-транзисторе; такие схемы менее
критичны к напряжению питания (2-18 В).
реимущества:
входное сопротивление порядка 1012
Ом, т.е ток входной цепью фактически не
потребляется; потребляемая мощность
связанна лишь с утечкой в полевом
моп-транзисторе; такие схемы менее
критичны к напряжению питания (2-18 В).
Недостатки: изначально низкое быстродействие (до 0,1 сек).
