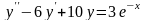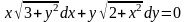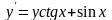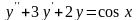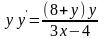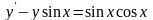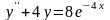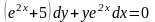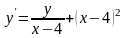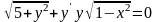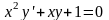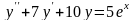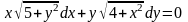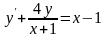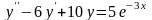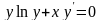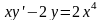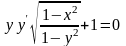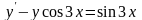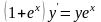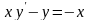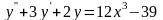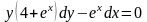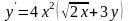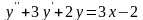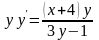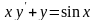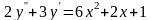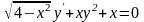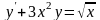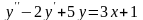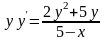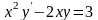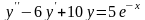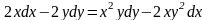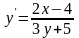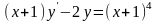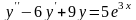- •Вища математика
- •5.05010201 «Обслуговування комп’ютерних систем і мереж»
- •5.05070103 «Електропостачання»
- •Методичні рекомендації для самостійного вивчення модуля №1 «Лінійна алгебра та аналітична геометрія»
- •Термінологічний словник.
- •Варіанти індивідуальних завдань.
- •Методичні рекомендації для самостійного вивчення модуля №2 «Комплексні числа. Основи диференціального числення» Теми для самостійного вивчення.
- •Термінологічний словник.
- •Диференціювання складних функцій з кількома змінними
- •Варіанти індивідуальних завдань.
- •Питання для самоконтролю.
- •Методичні рекомендації для самостійного вивчення модуля №3 «Інтегральне числення.» Теми для самостійного вивчення.
- •Термінологічний словник.
- •Формула Ньютона - Лейбниця для обчислення визначених інтегралів
- •Формули для розв’язування прикладних задач
- •Варіанти індивідуальних завдань.
- •Питання для самоконтролю.
- •Вимоги щодо виконання контрольної роботи
- •Література з вищої математики, що є у бібліотеці коледжу.
- •Питання до колоквіуму з теми «Елементи лінійної алгебри та аналітичної геометрії»
Варіанти індивідуальних завдань.
Обчислити невизначені інтеграли.
а)
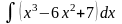 б)
б)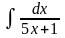 в)
в)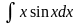
а)
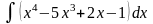 б)
б)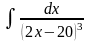 в)
в)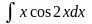
а)
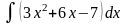 б)
б)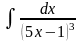 в)
в)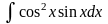
а)
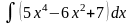 б)
б)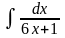 в)
в)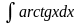
а)
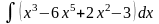 б)
б)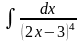 в)
в)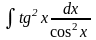
а)
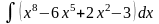 б)
б)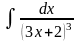 в)
в)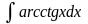
а)
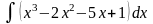 б)
б)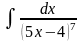 в)
в)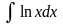
а)
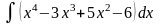 б)
б)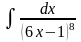 в)
в)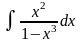
а)
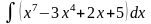 б)
б)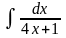 в)
в)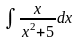
а)
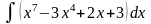 б)
б)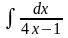 в)
в)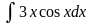
а)
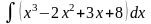 б)
б)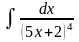 в)
в)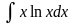
а)
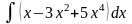 б)
б)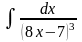 в)
в)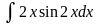
а)
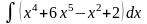 б)
б)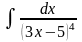 в)
в)
а)
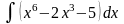 б)
б)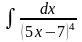 в)
в)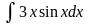
а)
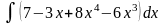 б)
б)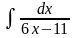 в)
в)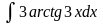
а)
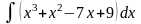 б)
б)
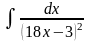 в)
в)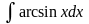
а)
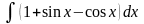 б)
б)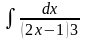 в)
в)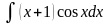
а)
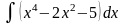 б)
б)
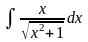 в)
в)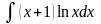
а)
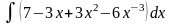 б)
б)
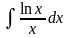 в)
в)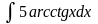
а)
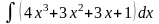 б)
б)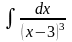 в)
в)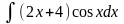
Обчислити визначені інтеграли.
а)
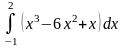 б)
б)
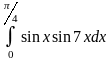
а)
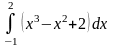 б)
б)
а)
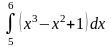 б)
б)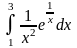
а)
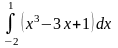 б)
б)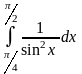
а)
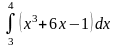 б)
б)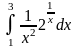
а)
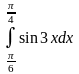 б)
б)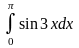
а)
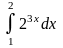 б)
б)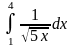
а)
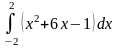 б)
б)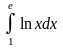
а)
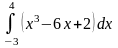 б)
б)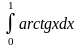
а)
 б)
б)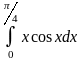
а)
 б)
б)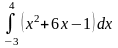
а)
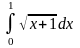 б)
б)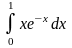
а)
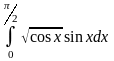 б)
б)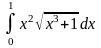
а)
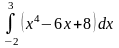 б)
б)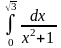
а) б)
а)
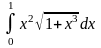 б)
б)
а)
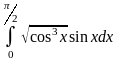 б)
б)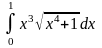
а)
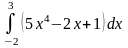 б)
б)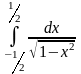
а)
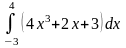 б)
б)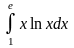
а)
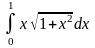 б)
б)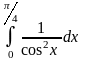
.
Обчислити площу фігури, обмеженої лініями:
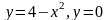 ;
;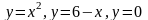 ;
;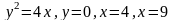
 ;
; ;
; ;
;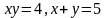 ;
;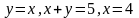 ;
;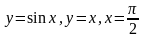 ;
;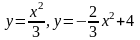 ;
;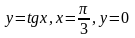 ;
;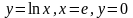 ;
;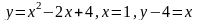 ;
;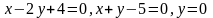 ;
;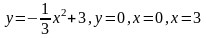 ;
;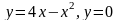 ;
; ;
;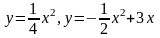 ;
;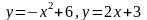 ;
;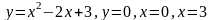 .
.
Знайти градієнт функції в точці М.
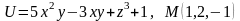 .
.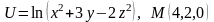 .
.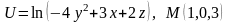 .
.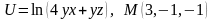 .
.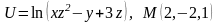 .
.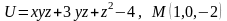 .
.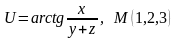 .
.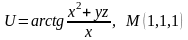 .
.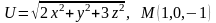 .
.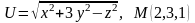 .
. .
..
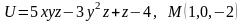 .
. .
.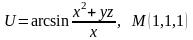 .
.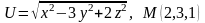 .
.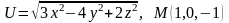 .
.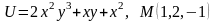 .
.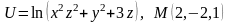 .
.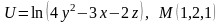 .
.
Знайти екстремуми функції
Дослідити збіжність числових рядів:
Знайти область збіжності степеневого ряду:
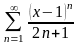
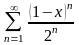
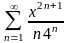
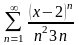
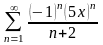
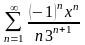
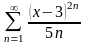
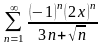
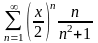
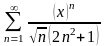
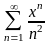
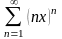
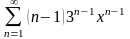
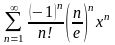

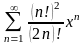
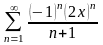
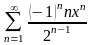
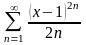
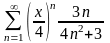 .
.
Знайти загальний розв’язок диференціальних рівнянь.
б) в) |
8.11а)
б)
в)
|
б) в) |
8.12а)
б)
в) |
б) в)
|
8.13а)
б) |
б) в) |
8.14
а)
б)
в) |
б) в) |
8.15а)
б)
в |
8.6
а) б) в) |
8.16
а)
б) в)
|
8.7
а) б) в) |
8.17а)
б)
в)
|
8.8
а) б) в)
|
8.18а)
б)
в) |
б) в) |
б)
в) |
8.10
а) б) в)
|
8.20
а)
б)
в)
|
Питання для самоконтролю.
1. Метод інтегрування дробово-раціональних функцій.
2. Метод інтегрування деяких тригонометричних функцій.
3. Метод інтегрування деяких ірраціональних функцій.
4. Інтегрування способом підстановки.
5. Інтегрування способом за частинами.
6. Означення визначеного інтеграла, його геометричний і фізичний зміст, умови існування. Обчислення визначених інтегралів за формулою Ньютона – Лейбніца.
7. Заміна змінної і інтегрування частинами у визначеному інтегралі.
8 Застосування визначеного інтегралу до розв’язання деяких задач геометрії: обчислення площі плоскої фігури, довжини лінії, об’єму тіла обертання.
9. Числові ряди. Збіжність і сума ряду. Необхідна умова збіжності.
10. Ряди з додатними членами. Ознаки збіжності: ознаки порівняння Даламбера.
11. Знакопочережні ряди. Абсолютна і умовна збіжність.
12. Ряди Тейлора і Маклорена.

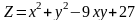
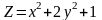
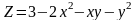
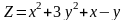
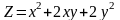
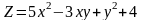


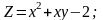
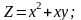
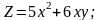
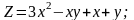
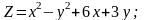
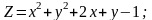
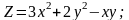

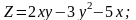

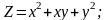
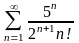
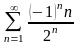
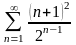
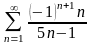
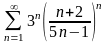
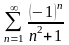
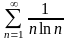
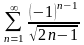
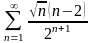
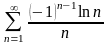
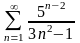
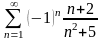
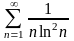
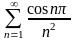
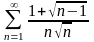
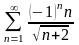
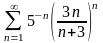

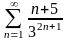
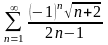
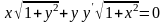 ;
;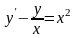 ;
;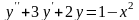 .
.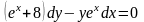
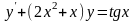
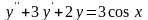 .
.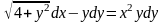 ;
;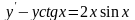 ;
;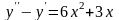
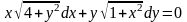 ;
;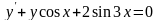 ;
;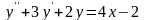 .
.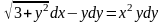
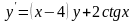
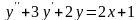
 ;
;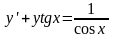 в)
в)