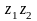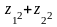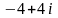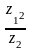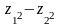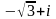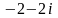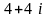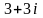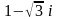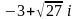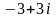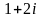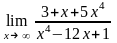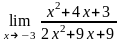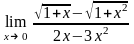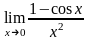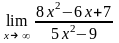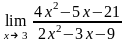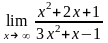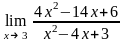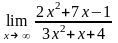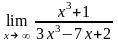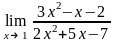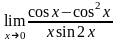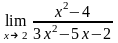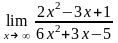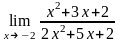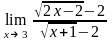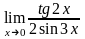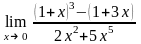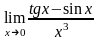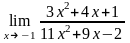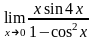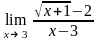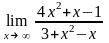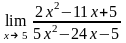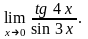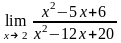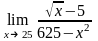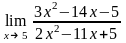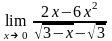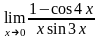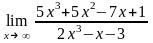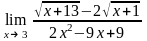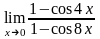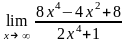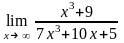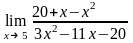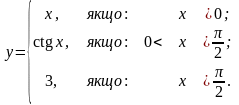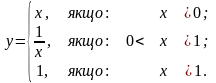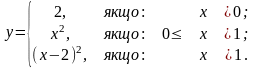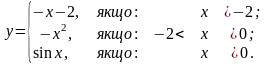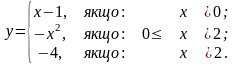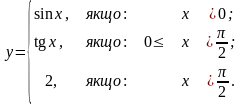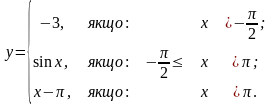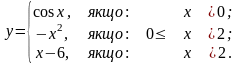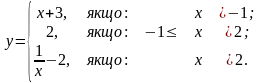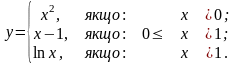- •Вища математика
- •5.05010201 «Обслуговування комп’ютерних систем і мереж»
- •5.05070103 «Електропостачання»
- •Методичні рекомендації для самостійного вивчення модуля №1 «Лінійна алгебра та аналітична геометрія»
- •Термінологічний словник.
- •Варіанти індивідуальних завдань.
- •Методичні рекомендації для самостійного вивчення модуля №2 «Комплексні числа. Основи диференціального числення» Теми для самостійного вивчення.
- •Термінологічний словник.
- •Диференціювання складних функцій з кількома змінними
- •Варіанти індивідуальних завдань.
- •Питання для самоконтролю.
- •Методичні рекомендації для самостійного вивчення модуля №3 «Інтегральне числення.» Теми для самостійного вивчення.
- •Термінологічний словник.
- •Формула Ньютона - Лейбниця для обчислення визначених інтегралів
- •Формули для розв’язування прикладних задач
- •Варіанти індивідуальних завдань.
- •Питання для самоконтролю.
- •Вимоги щодо виконання контрольної роботи
- •Література з вищої математики, що є у бібліотеці коледжу.
- •Питання до колоквіуму з теми «Елементи лінійної алгебри та аналітичної геометрії»
Методичні рекомендації для самостійного вивчення модуля №2 «Комплексні числа. Основи диференціального числення» Теми для самостійного вивчення.
1. Комплексні числа, їх мнима та дійсна частини. Геометричне зображення комплексного числа.
2. Дії над комплексними числами та їх геометрична інтерпритація.
3. Тригонометрична форма комплексного числа.
4. Дії з комплексними числами , які записані в тригонометричній формі.
5. Показникова форма комплексного числа.
6. Дії з комплексними числами, які записані в показниковій формі.
7. Функції область визначення. Елементарні функції.
8. Границя послідовності. Нескінченно малі величини.
9. Границя функції. Особливості границі. Розкриття невизначеностей.
10. Неперервність функції. Властивості неперервних функцій. Розриви функцій.
11. Похідна функції. Геометричний та механічний зміст похідної. Правила диференціювання.
12. Похідні вищих порядків. Теореми про диференціювання функції. Правило Лопіталя. Формула Тейлора.
13. Дослідження функції та побудова графіків.
14. Частинні похідні функції. Повний диференціал. Правила диференціювання.
15. Похідна за напрямом . Градієнт. Опуклість та вгнутість функції. Екстремуми функції. Необхідні та достатні умови екстремуму.
Термінологічний словник.
Алгебраїчна
форма комплексного числа:
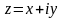
Модуль
комплексного числа:

Аргумент
комплексного числа:

Дії над комплексними числами в алгебраїчній формі:
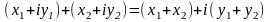 ;
; ;
;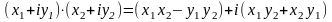 ;
;
4) ,
при умові, що
,
при умові, що
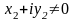 .
.
Тригонометрична
форма:

Дії над комплексними числами в тригонометричній формі:
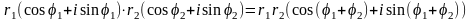 ;
; ;
; ;
; .
.
Показникова
форма:

Дії над комплексними числами в показниковій формі:
 ;
;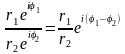 ;
; ;
;
Перша
важлива границя
 .
.
Друга
важлива границя
 .
.
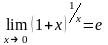 .
.
Правила диференціювання
Якщо.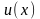 та
та
 - диференційовані функції, то
- диференційовані функції, то
Таблиця похідних
|
|
Похідна складної функції
Похідна
складної функції
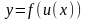 дорівнює
добутку похідної цієї функції за
проміжною змінною и
на похідну проміжної змінної и
за
змінною х.
Тобто,
дорівнює
добутку похідної цієї функції за
проміжною змінною и
на похідну проміжної змінної и
за
змінною х.
Тобто,


 -
геометричний
зміст похідної
-
геометричний
зміст похідної
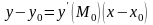 -
рівняння
дотичної
-
рівняння
дотичної
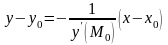 -
рівняння
нормалі.
-
рівняння
нормалі.
Диференціювання складних функцій з кількома змінними
1.
2.
,
де
3.
|
4.
,
|
5.
|
Варіанти індивідуальних завдань.
Записати в тригонометричній та показниковій формах комплексні числа
 і
і
 .
Обчислити
.
Обчислити
 .
.
№ |
|
|
|
|
|
№ |
|
|
|
|
|
|
|
|
|
|
|
1.11 |
|
|
|
|
|
|
|
|
|
|
|
1.12 |
|
|
|
|
|
|
|
|
|
|
|
1.13 |
|
|
|
|
|
|
|
|
|
|
|
1.14 |
|
|
|
|
|
|
|
|
|
|
|
1.15 |
|
|
|
|
|
|
|
|
|
|
|
1.16 |
|
|
|
|
|
|
|
|
|
|
|
1.17 |
|
|
|
|
|
|
|
|
|
|
|
1.18 |
|
|
|
|
|
|
|
|
|
|
|
1.19 |
|
|
|
|
|
|
|
|
|
|
|
1.20 |
|
|
|
|
Завдання 2. Знайти область визначення функцій.
1.
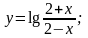 2. y =
2. y =
 3. y =
3. y =
4.
y =
 5. y = lg
5. y = lg 6.y =
6.y =
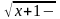
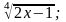
7.
y =
 8. y =
8. y =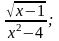 9. y =
9. y =
10.
y = arccos 11. y =
11. y =
 12. y =
12. y =
13.
y = arccos(2x-3) +
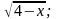 14. y = 2
14. y = 2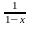 +
arcsin
+
arcsin 15. y = e
15. y = e
16.
y = arcsin
17. y =
 log
log (8-4x);
18. y =
(8-4x);
18. y =

19.y
= arccos 20. y =
20. y =
 21. y = log
21. y = log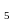

22.
y = arccos 23. y =
23. y =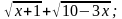 24. y =
24. y =
 log
(x
log
(x
25.
y =
 ;
26. y =
;
26. y =
 27. y =
27. y =
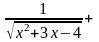 arcsin
arcsin
28.
y
= e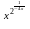 +
+ 29.y
=
29.y
=
 30. y
= log
30. y
= log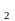

Завдання 3. Обчислити границі функцій не використовуючи правило Лопіталя:
Вар |
а) |
б) |
в) |
г) |
1 |
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
4 |
|
|
|
|
5 |
|
|
|
|
6 |
|
|
|
|
7 |
|
|
|
|
8 |
|
|
|
|
9 |
|
|
|
|
10 |
|
|
|
|
11 |
|
|
|
|
12 |
|
|
|
|
13 |
|
|
|
|
14 |
|
|
|
|
15 |
|
|
|
|
16 |
|
|
|
|
17 |
|
|
|
|
18 |
|
|
|
|
19 |
|
|
|
|
20 |
|
|
|
|
Завдання 4. Дослідити на неперервність функцію та класифікувати точки розриву:
1).
|
2). |
3).
|
4).
|
5).
|
6).
|
7).
|
8).
|
9).
|
10).
|
11).
|
12). |
13). |
14).
|
15).
|
16).
|
17).
|
18).
|
19).
|
20).
|
21).
|
22).
|
23). |
24). |
25).
|
26).
|
27).
|
28).
|
29).
|
30).
|
Завдання 5. Знайти похідні даних функцій:
Частина 1.
а)
 ,
б)
,
б) , в)
, в)

а)
 б)
б) ,
в)
,
в)
а)
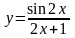 б)
, в)
б)
, в)
а)
 б)
б) в)
в)
а)
 б)
б)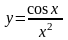 в)
в)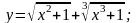
а)
 б)
б)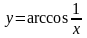 в)
в)
а)
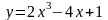 б)
б) в)
в)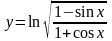 ;
;
а)
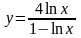 б)
в) y = ln(ex
+
б)
в) y = ln(ex
+

а)
 б)
б) в)
в)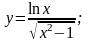
а)
 б)
б) в)
в)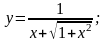
а)
 б)
б)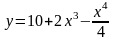 в) y = tg2
(x3+1);
в) y = tg2
(x3+1);а)
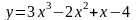 б)
б) в) y = arctg
в) y = arctg

а)
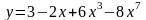 б)
б)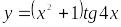 в) y = arctg
в) y = arctg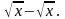
а)
 б)
б)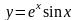 в)
y = sin2
3x
в)
y = sin2
3x
а)
 б)
б) в)
y =
в)
y =
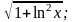
а)
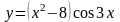 б)
б) в) y = arctg
в) y = arctg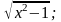
а)
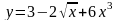 б)
в)
б)
в)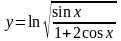 ;
;а)
 б)
б) в)
в)

а)
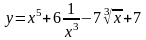 б)
б) в)
в)
а)
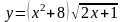 б)
б)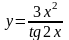 в)
в)
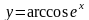
Частина 2.
1). 



2). 

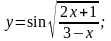
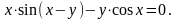
3). 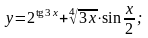
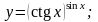
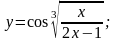

4). 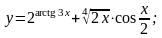

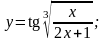

5). 


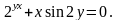
6). 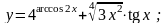



7). 

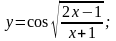

8). 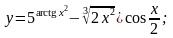
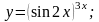


9). 
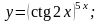

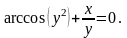
10). 


11). 
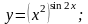
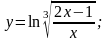

12). 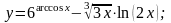
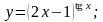
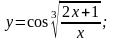
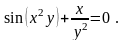
13). 
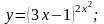


14). 


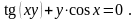
15). 
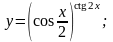

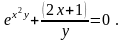
16). 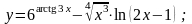
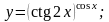

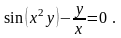
17). 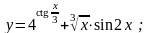
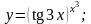
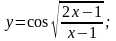
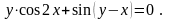
18). 



19). 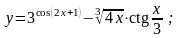



20). 



21). 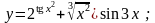
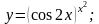


22). 


23). 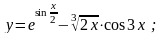



24). 
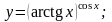


25). 



26). 



27). 



28). 

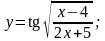
29). 
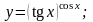
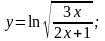
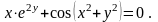
30). 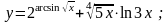

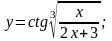

Завдання 6. Дослідити функції за допомогою диференціального числення та побудувати їх графіки:
1). 

2). 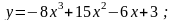

3). 

4). 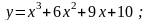

5). 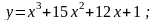
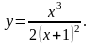
6). 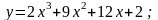

7). 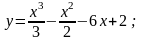
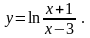
8). 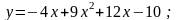

9). 

10). 

11). 
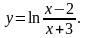
12). 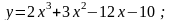
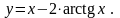
13). 
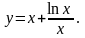
14). 
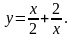
15). 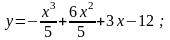
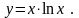
16). 
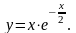
17). 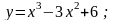
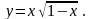
18). 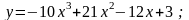
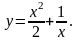
19). 

20). 

21). 
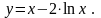
22). 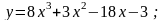
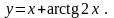
23). 
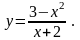
24). 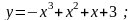

25). 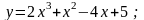

26). 

27). 
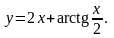
28). 
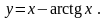
29). 

30). 
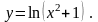
Завдання 7.
Розв’язати задачу:
Коштовність обладнання підприємства зменшується пропорційно швидкості зменшення коштовності обладнання. Визначте коштовність обладнання через три роки, якщо спочатку вона складала 20400 гривень
Коштовність обладнання підприємства за п’ять років зменшилась до 20500 гривень. Обчислити, якою вона була спочатку, якщо коштовність обладнання зменшується пропорційно швидкості зменшення коштовності обладнання.
Визначте найбільшу площу стоянки, яку можна огородити тином довжиною 200 метрів.
Вікно має форму прямокутника, закінченим півколом. При заданому периметрі знайти такі його розміри, щоб воно пропускало найбільше світла. Р=6м.
Необхідно зробити дерев’яну коробку з квадратним дном без кришки найбільшого об’єму. Знайдіть розміри коробки, якщо площа поверхні дерева, з якого необхідно зробити коробку складає 80см.
Знайдіть розміри будівлі, на яку буде витрачено найменша кількість цегли, якщо висота будівлі складає 3м, площа 30м .
Необхідно виділити прямокутну площину землі в 1024м2, огородити її тином та розділити загородкою на три рівних частини паралельно одній із сторін площини. Які потрібні розміри площини, щоб на побудову тинів пішла найменша кількість матеріалу.
Трати на рекламу впливають на валовий прибуток R(a) відповідно закону: R(a)=R(1+a1/3)? Де R- прибуток у відсутності реклами. При яких значеннях R оптимальні трати на рекламу перебільшать прибуток за відсутністю реклами?
Прямокутний лист жерсті має лінійні розміри 5*8дм. У чотирьох його кутах вирізають однакові квадрати і роблять відкриту коробку, загинаючи краї під прямим кутом. Яка максимально можлива місткість цієї коробки?
Знайти вираз для об’єма реалізованої продукції у=у(t) та його значення при t=2, якщо відомо, що крива попиту має вид: p(y)=3-2y, норма акселерації 1/l=1.5, норма інвестицій m=0.6, у(0)=1.
Коштовність обладнання підприємства зменшується пропорційно швидкості зменшення коштовності обладнання. Визначте коштовність обладнання через три роки, якщо спочатку вона складала 20400 гривень
Коштовність обладнання підприємства за п’ять років зменшилась до 20500 гривень. Обчислити, якою вона була спочатку, якщо коштовність обладнання зменшується пропорційно швидкості зменшення коштовності обладнання.
Визначте найбільшу площу стоянки, яку можна огородити тином довжиною 200 метрів.
Вікно має форму прямокутника, закінченим півколом. При заданому периметрі знайти такі його розміри, щоб воно пропускало найбільше світла. Р=6м.
Необхідно зробити дерев’яну коробку з квадратним дном без кришки найбільшого об’єму. Знайдіть розміри коробки, якщо площа поверхні дерева, з якого необхідно зробити коробку складає 80см.
Знайдіть розміри будівлі, на яку буде витрачено найменша кількість цегли, якщо висота будівлі складає 3м, площа 30м .
Необхідно виділити прямокутну площину землі в 1024м2, огородити її тином та розділити загородкою на три рівних частини паралельно одній із сторін площини. Які потрібні розміри площини, щоб на побудову тинів пішла найменша кількість матеріалу.
Трати на рекламу впливають на валовий прибуток R(a) відповідно закону: R(a)=R(1+a1/3)? Де R- прибуток у відсутності реклами. При яких значеннях R оптимальні трати на рекламу перебільшать прибуток за відсутністю реклами?
Прямокутний лист жерсті має лінійні розміри 5*8дм. У чотирьох його кутах вирізають однакові квадрати і роблять відкриту коробку, загинаючи краї під прямим кутом. Яка максимально можлива місткість цієї коробки?
Знайти вираз для об’єма реалізованої продукції у=у(t) та його значення при t=2, якщо відомо, що крива попиту має вид: p(y)=3-2y, норма акселерації 1/l=1.5, норма інвестицій m=0.6, у(0)=1.
Коштовність обладнання підприємства зменшується пропорційно швидкості зменшення коштовності обладнання. Визначте коштовність обладнання через три роки, якщо спочатку вона складала 20400 гривень
Коштовність обладнання підприємства за п’ять років зменшилась до 20500 гривень. Обчислити, якою вона була спочатку, якщо коштовність обладнання зменшується пропорційно швидкості зменшення коштовності обладнання.
Визначте найбільшу площу стоянки, яку можна огородити тином довжиною 200 метрів.
Вікно має форму прямокутника, закінченим півколом. При заданому периметрі знайти такі його розміри, щоб воно пропускало найбільше світла. Р=6м.
Необхідно зробити дерев’яну коробку з квадратним дном без кришки найбільшого об’єму. Знайдіть розміри коробки, якщо площа поверхні дерева, з якого необхідно зробити коробку складає 80см.
Завдання 8. Перевірити слідуючи рівності.
1.
y при z
= e
при z
= e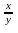
2.
 при z
=
при z
=
 sin
sin
3.
 при
z
=
при
z
=
4. при z
=
при z
=
Знайти диференціали другого порядку від функцій:
5.
z
= 6. z
=
6. z
= 7. z
=
7. z
=
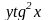
8.
z
= ln(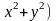 9. z
=
9. z
=
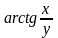 10. z
=
10. z
=
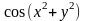
Впевніться, що для;
11.z
=
 12. z
=
12. z
=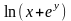 13. z
=
13. z
=

14.z
=
 15. z
= y
15. z
= y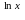
16.
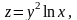 Знайти
Знайти
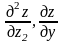
17.
 Знайти
Знайти

18.
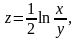 Знайти
Знайти

19.
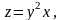 Знайти
Знайти
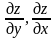
20.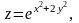 Знайти
Знайти
Зайти
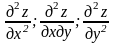 від
функцій:
від
функцій:
21.
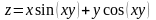 22.
22.
23.
 24.
24.
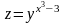


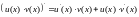

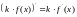
 .
. .
. .
. .
. .
. .
. .
. .
.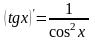 .
. .
. .
. .
. .
.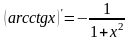
 ,
де
,
де
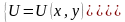 ,
то
,
то
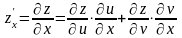 ,
, .
. ,
то
,
то
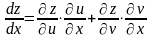 .
. ,
де
,
де
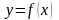 ,
то
,
то
 .
. .
. ,
у точках неперервності.
,
у точках неперервності.