2.3 Аппроксимация временной характеристики объекта регулирования

По виду графического изображения временной характеристики определяем к какому типовому звену или сочетанию звеньев относиться наша кривая. Чаще всего это звено инерционное без транспортного запаздывания ( одноемкостной объект с самовыравниванием), математическое изображение h(t) = K(1 – e^-t/T).

Подставляя значения параметров объекта регулирования, найденные по усредненной динамической характеристике в математические выражения, находим координаты значений аппроксимированной временной характеристики переходного процесса нашего объекта регулирования. Строим аппроксимированную характеристику.

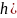
Время	0	1	2	3	4	5	6	7	8	9	10	11	12
h(t)усред.	0	1,72	2,55	3,02	3,24	3,42	3,45	3,51	3,56	3,55	3,52	3,53	3,53
h(t)апрокс.	0	1,36	2,21	2,73	3,06	3,26	3,39	3,47	3,52	3,55	3,56	3,58	3,58

2.4 Оценка точности получения экспериментальной временной характеристики

Определяем приведенную погрешность между экспериментальной и аппроксимированной динамическими характеристиками по формуле:

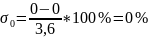
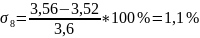
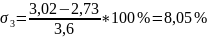
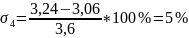
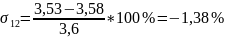
Для более точной и объективной оценки правильности снятия кривых разгона определяем среднеквадратическое отклонение кривых по формуле:

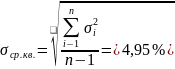
σ_ср.кв ≤ 5% это значит кривые разгона сняты правильно и параметры, найденные из опытной динамической характеристики, можно использовать для дальнейших расчетов.

Передаточная функция объекта описывается формулой:

К=3,6 °C/%

Т=2,1 мин

2.5 Проверка объекта регулирования на устойчивость

2.5.1 Алгебраический метод (корневой)

При этом методе знаменатель передаточной функции (характеристическое уравнения) приравниваем к нулю. Находим корни и если они отрицательные и вещественные, то согласно критерию Ляпунова объекта является устойчивым.

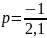
Из решения видно, что корни характеристического уравнения вещественные отрицательные. Следовательно, объект управления устойчивый.

2.5.2 Частотный метод (по кривой годографа)

Для одноёмкостных статических объектов с передаточной функцией

где Т - постоянная времени. Построение годографа начинается с замены p на iω. Получим частотную передаточную функцию

Умножим числитель и знаменатель на комплексно - сопряженное значение знаменателя и получим

Выделим в этом выражении действительную и мнимую часть

Отсюда получим

Для построения годографа изменяем частоту от ω=0 до ω=∞

Tоб	Коб	ω	Re	Im
2,1	3,6	0	1	0
2,1	3,6	0,1	0,9577627	-0,20113
2,1	3,6	0,2	0,850051	-0,357021
2,1	3,6	0,3	0,7158709	-0,450999
2,1	3,6	0,4	0,5863039	-0,492495
2,1	3,6	0,5	0,4756243	-0,499405
2,1	3,6	0,6	0,3864585	-0,486938
2,1	3,6	0,7	0,3163656	-0,465057
2,1	3,6	0,8	0,2616157	-0,439514
2,1	3,6	0,9	0,2187179	-0,413377
2,1	3,6	1	0,1848429	-0,38817
2,1	3,6	1,2	0,136047	-0,342838
2,1	3,6	1,4	0,1036957	-0,304865
2,1	3,6	1,6	0,0813696	-0,273402
2,1	3,6	1,8	0,0654091	-0,247246
2,1	3,6	2	0,0536481	-0,225322
2,1	3,6	2,5	0,0350109	-0,183807
2,1	3,6	3	0,0245761	-0,154829
2,1	3,6	4	0,0139743	-0,117384
2,1	3,6	5	0,0089888	-0,094382
2,1	3,6	10	0,0022624	-0,047511
2,1	3,6	20	0,0005666	-0,023796
2,1	3,6	25	0,0003627	-0,019041

Из годографа видно, что объект устойчивый.

ЗАКЛЮЧЕНИЕ

Из расчётной части видно, что объект (контур температуры) описывается апериодическим звеном. И имеет следующую передаточную функцию.

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

1. Б.З. Барласов, В.И. Ильин. Наладка приборов и средств автоматизации.

Москва: Высшая школа, 1980.

2. В.И. Горшков. Автоматическое управление.

Москва: Академия, 2003.

3. А.С. Клюев. Автоматическое регулирование.

Москва: Энергия, 1986.

4. К.П. Широков, М.Г. Богусловский. Международная система единиц.

Москва: Издательство стандартов, 1984.

5. В.Ю. Шишмарев. Средства измерений.

Москва: Академия, 2006.

6. В.В. Шувалов и др. Автоматизация производственных процессов в химической промышленности.

Москва: Химия, 1991.

7. Каталог продукции ПГ «Метран», 2006.

8. Каталог продукции ООО «Теплоприбор», 2006.

9. Каталог продукции ООО «Элемер», 2007.

4