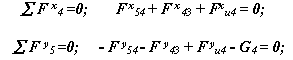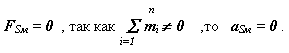Кинетостатический силовой расчет типовых механизмов.

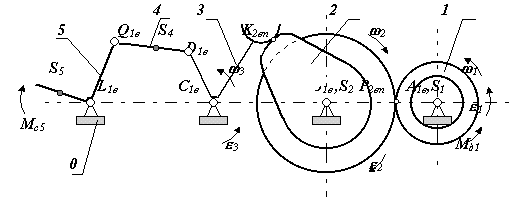
Рассмотрим механизм, состоящий из трех соединенных последовательно простых механизмов: зубчатой передачи, кулачкового механизма и четырехшарнирного рычажного механизма (рис. 4.6).

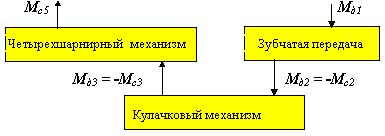
Представим этот механизм в виде комбинации типовых механизмов:

Рис. 4.7

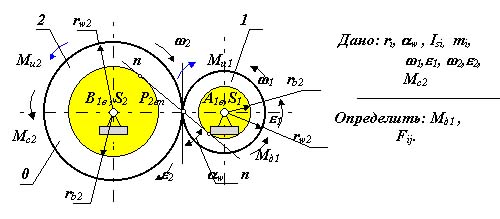
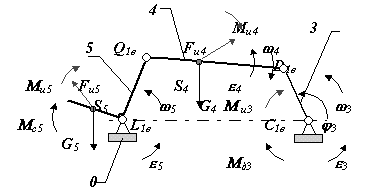
1.Кинетостатический расчет зубчатой передачи (метод планов сил). Для примера рассмотрим цилиндрическую эвольвентную зубчатую передачу. При проведении расчета нам необходима информация о размерах зубчатых колес и положении контактной нормали в высшей КП. Для эвольвентной передачи необходимо знать радиусы основных r_b1 ,r_b2или начальных окружностей r_w1 ,r_w2, и угол зацепления _w, т.к r_bi =r_w1 cos _w . По этим размерам в масштабе изображается кинематическая схема механизма, на которую наносятся все известные силы и моменты. Главные вектора и моменты сил инерции рассчитываются по формулам

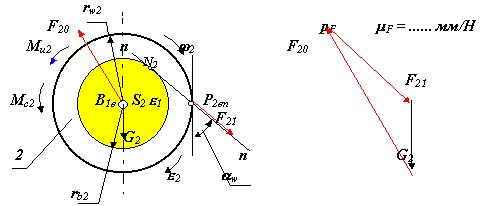
так как кинематические параметры a_Si, _i механизма при кинетостатическом расчете заданы. Определим подвижность, число избыточных связей в механизме, а также число неизвестных в силовом расчете: т.е в нашем механизме неизвестно 6 компонент реакций, для решения задачи силового расчета необходимо составить 6 уравнений кинетостатики. Структурный анализ механизма показывает что механизм состоит из одного первичного механизма (звено 1 и стойка) и монады (структурной группы, состоящей из одного звена 2). Анализ начнем со второго звена, так как о нем больше известно. Расчетная схема для звена 2 приведена на рис. 4.9.

Рис. 4.8

>Уравнения равновесия для звена 2: векторное уравнение силового равновесия

уравнение моментов относительно точки В

Рис. 4.11

Вначале решается уравнение моментов и определяется величина силы F₂₁. Затем графически в масштабе _F, по векторному уравнению сил строится многоугольник (рис.4.10), из которого определяется величина и направление реакции F₂₀.

2.1. Звено 1. Расчетная схема для звена 1 приведена на рис. 4.11. Уравнения равновесия для звена 1: векторное уравнение силового равновесия

уравнение моментов относительно точки А

Рис. 4.11

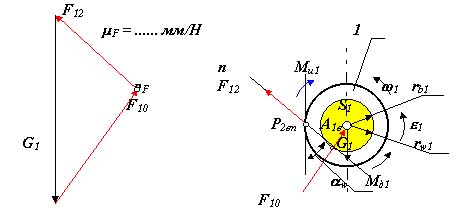
Для звена 1 движущий момент M_д1рассчитывается по уравнению моментов, а величина и направление реакции F₁₀ определяется графически (рис.4.12), построением плана сил в масштабе _F.

Примечание: Кулачковый механизм рассчитывается аналогично, поэтому его силовой расчет не рассматриваем.

Кинетостатический расчет четырехшарнирного механизма (метод проекций или аналитический).

Изобразим расчетную схему механизма и нанесем на нее все внешние силы и моменты (рис.4.13).

Рис. 4.13

Постановка задачи. Дано: >l_i, ₃, ₃, ₃, m_i, I_si, M_c5. Определить:F_ij, M_д3.

1. Определение подвижности механизма, числа избыточных связей в КП и числа неизвестных в силовом расчете.

2. Определение скоростей и ускорений звеньев и центров их масс.

3. Определение главных векторов и главных моментов сил инерции.

4. Кинетостатический расчет механизма.

4.1 Звено 5 (рис. 4.14). Уравнения силового равновесия в проекциях на оси координат

и сумма моментов сил относительно точки L

4.2 Звено 4. (рис. 4.15). Уравнения силового равновесия в проекциях на оси координат

и сумма моментов сил относительно точки Q

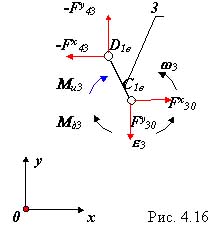
4.3 Звено 4. (рис. 4.16).

Уравнения силового равновесия в проекциях на оси координат

и сумма моментов сил относительно точки C

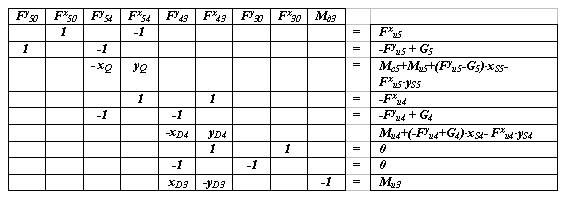
Таким образом мы составили систему 9-и уравнение с 9-ю неизвестными. При составлении этой системы были учтены равенства действия и противодействия F_ij = - F_ji ( без учета этих равенств общее число неизвестных и уравнений системы 18 ). Составим матрицу этой системы:

Из решения этой системы уравнений определяются реакции в КП и движущий момент М_д3

Примечание: Более подробно с силовым расчетом рычажных механизмов Вы познакомитесь на упражнениях и при выполнении 2-го домашнего задания.

ЛЕКЦИЯ 5

Краткое содержание: Вибрации и колебания в машинах и механизмах, виброактивность и виброзащита. Понятие о неуравновешенности звена и механизма, статической и динамической уравновешенности механической системы. Статическое уравновешивание рычажных механизмов. Метод замещающих масс. Полное и частичное статическое уравновешивание механизма. Ротор и виды его неуравновешенности: статическая, моментная и динамическая. Балансировка роторов при проектировании. Балансировочные станки.

Вибрации и колебания в машинах и механизмах.

При движении механической системы под действием внешних сил в ней могут возникать механические колебания или вибрации. Причинами возникновения вибраций могут быть периодические изменения сил (силовое возмущение), перемешений (кинематическое возмущение) или инерционных характеристик (параметрическое возмущение). Вибрацией ( от лат. vibratio - колебание ) называют мех*анические колебания в машинах или механизмах. Колебание - движение или изменение состояния, обладающие той или иной степенью повторяемости или периодичностью. Если источник возникновения вибраций определяется внутренними свойствами машины или механизма, то говорят о его виброактивности. Чтобы вибрации механизма не распространялись на окружающие его системы или чтобы защитить механизм от вибраций, воздействующих на него со стороны внешних систем, применяются различные методы виброзащиты. Различают внешнюю и внутреннюю виброактивность. Под внутренней виброактивностью понимают колебания возникающие внутри механизма или машины, которые происходят по его подвижностям или обобщенным координатам. Эти колебания не оказыват непосредственного влияния на окрущающую среду. При внешней виброактивности изменение положения механизма приводит к изменению реакций в опорах (т.е. связях механизма с окружающей средой) и непосредственному вибрационному воздействию на связанные с ним системы. Одна и основных причин внешней виброактивности - неуравновешенность его звеньев и механизма в целом.

Понятие о неуравновешенности механизма (звена).

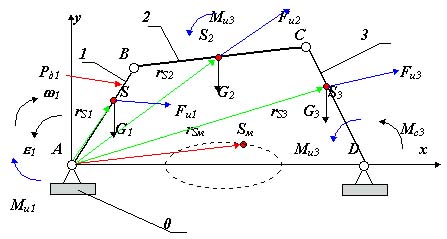
Неуравновешенным будем называть такой механизм (или его звено), в котором при движении центр масс механизма (или звена) движется с ускорением. Так как ускоренное движение системы возникает только в случае, если равнодействующая внешних силовых воздействий не равна нулю. Согласно принципу Д’Аламбера, для уравновешивания внешних сил к системе добавляются расчетные силы - силы и моменты сил инерции. Поэтому уравновешенным будем считать механизм, в котором главные вектора и моменты сил инерции равны нулю, а неуравновешенным механизм, в котором эти силы неравны нулю. Для примера рассмотрим четырехшарнирный механизм (рис. 5.1).

Механизм будет находится в состоянии кинетостатического равновесия, если сумма действующих на него внешних сил и моментов сил (включая силы и моменты сил инерции) будет равна нулю

Уравновешенность является свойством или характеристикой механизма и не должна зависеть от действующих на него внешних сил. Если исключить из рассмотрения все внешние силы, то в уравнении равновесия останутся только инерционные составляющие, которые определяются инерционными параметрами механизма - массами и моментами инерции и законом движения (например, центра масс системы). поэтому уравновешенным считается механизм для которого главный вектор и главный момент сил инерции равны нулю:

Неуравновешенность - такое состояние механизма при котором главный вектор или главный момент сил инерции не равны нулю. Различают:

• статическую неуравновешенность F_Sм не равно 0 ;

• моментную неуравновешенность M_имне равно 0 ;

• динамическую неуравновешенность F_Sм¹не равно 0 и M_имне равно 0 .

При статическом уравновешивании механизма необходимо обеспечить

Это условие можно выполнить если: скорость центра масс механизма равна нулю V_Sм=0или она постоянна по величине и направлению V_Sм= const. Обеспечить выполнение условия V_Sм = const в механизме практически невозможно. Поэтому при статическом уравновешивании обеспечивают выполнение условия V_Sм=0 . Это возможно, когда центр масс механизма лежит на оси вращения звена 1 - r_Sм= 0 или когда он неподвижен

r_Sм= const , где r_Sм= ( m₁*r_S1 + m₂*r_S2 + ... + m*r_Si )/ (m₁ + m₂ + ... + m_i).

На практике наиболее часто статическое уравновешивание проводят:

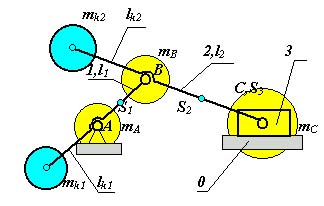
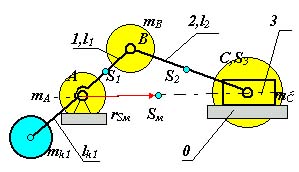
• выбирая симметричные схемы механизма (рис.5.2);

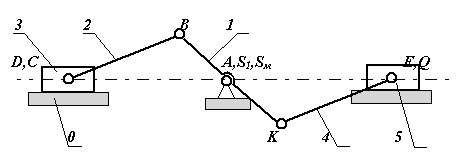
  Рис 5.2

• устанавливая на звеньях механизма противовесы (или корректирующие массы);

• размещая противовесы на дополнительных звеньях или кинематических цепях.

Метод замещающих масс.

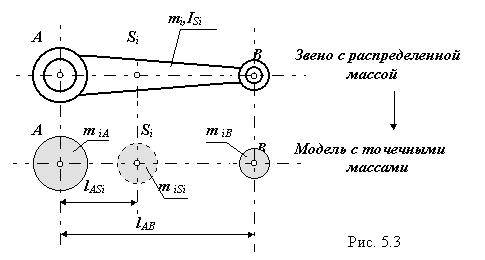
При использовании метода замещающих масс, звено механизма с распределенной массой заменяется расчетной моделью, которая состоит из точечных масс.

Условия перехода от звена с распределенной массой к модели с точечными массами.

• Сохранение массы звена: m _iA + m _iB = m_i .

• Сохранение положения центра масс l_ASi = const , m _iA *l_ASi = m _iB*(l_AB - l_ASi).

• Сохранение момента инерции m _iA*l_ASi² + m _iB *(l_AB - l_ASi)² = I_si.

Очевидно, что выполнить три условия системой с двумя массами невозможно, поэтому при статическом уравновешивании механизмов ограничиваются выполнением только двух первых условий. Чтобы обеспечить выполнение всех трех условий необходимо ввести третью массу m _iSi. Рассмотрим применение метода замещающих масс при полном и частичном статическом уравновешивании кривошипно-ползунного механизма.

Полное статическое уравновешивание кривошипно- ползунного механизма.

Рис 5.3

Постановка задачи:

Дано: l_AB, l_BC, l_AS1, l_BS2, l_CS3=0, m₁, m₂, m₃

Определить: m_k1, m_k2

Распределим массы звеньев по методу замещающих масс и сосредоточим их в центрах шарнировA,B,C.Тогда

m_B = m_B1 + m_B2 , m _C = m₃ + m_C2 , m_A = m_A1 ,

где m₁ = m_A1 + m_B1 - масса первого звена, распределенная между массами, сосредоточенными в точках В ;

m₂ = m_В2 + m - масса второго звена, распределенная между массами, сосредоточенными в точках В и С

Вначале проведем уравновешивание массы m_C корректирующей массой m_k2. Составим уравнение статических моментов относительно точки В для звеньев 2 и 3:

m _k2 l_k2 = m _C l_BC .

Задаемся величиной l_k2 и получаем корректирующую массу m _k2 = m _C *l_BC / l_k2 .

Затем уравновешиваем массы центр, которых после установки корректирующей массы расположился в точке В:

m_B ^* = m₂ + m_k2 + m₃ + m_B1.

Составляем уравнение статических моментов относительно точки А m _k1*l_k1 = m_В* _ l_АВ .

Задаемся величиной l_k1 и получаем корректирующую массу

m _k1 = m_В*l_АВ / l_k1.

Окончательно величины корректирующих масс для полного уравновешивания кривошипно-ползунного механизма

m _k2 = m _C *l_BC / l_k2 = ( m_С2 + m₃ )* l_BC / l_k2 ;

m _k1 = m_В*l_АВ / l_k1= (m₂ + m_k2 + m₃ + m_B1) *l_АВ / l_k1 .

Частичное статическое уравновешивание кривошипно-ползунного механизма.

Уравновешивание вертикальной составляющей главного вектора сил инерции.

Рис 5.5

Постановка задачи:

Дано: l_AB, l_BC, l_AS1, l_BS2, l_CS3=0,

m₁, m₂, m₃ Определить: m_k1

В этом случае необходимо добиться, чтобы центр масс механизма при движении перемещался вдоль направляющей ползуна (для схемы на рис. 5.5 по горизонтали). Для этого достаточно уравновесить только массу m_B .

Составляем уравнение статических моментов относительно точки А : m _k1 *l_k1 = m_В *l_АВ . Задаемся величиной l_k1 и получаем корректирующую массу m _k1 = m_В *l_АВ / l_k1. Окончательно величина корректирующей массы для уравновешивания вертикальной составляющей главного вектора сил инерции кривошипно-ползунного механизма

m _k1 = m_В *l_АВ / l_k1= (m _В2 + m_B1) *l_АВ / l_k1 .