Геометрические и кинематические характеристики механизма

Рис. 3.1

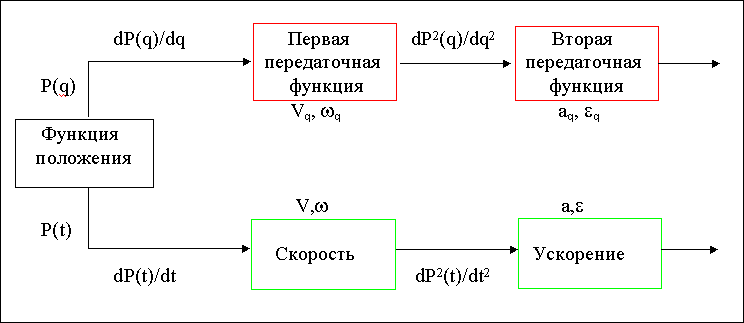
    Кинематическими передаточными функциями механизма называются производные от функции положения по обобщенной координате. Первая производная называется первой передаточной функцией или аналогом скорости (обозначается V_q,_q), вторая - второй передаточной функцией или аналогом ускорения (обозначается a_q, _q).

    Кинематическими характеристиками механизма называются производные от функции положения по времени. Первая производная называется скоростью (обозначается V, , вторая - ускорением (обозначается a, ).

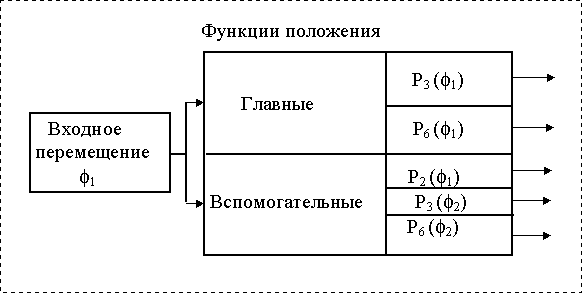
    Механизм с одной подвижностью имеет одно заданное входное движение и бесчисленное множество выходных ( движение любого звена или точки механизма ). Передаточные функции тех движений, которые в данном случае используются как выходные, называются главными, остальные - вспомогательными.

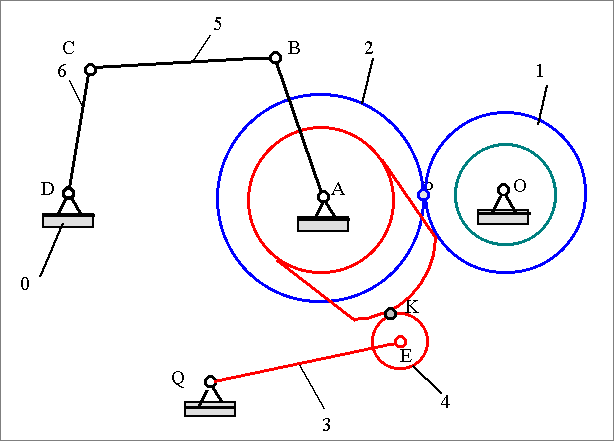
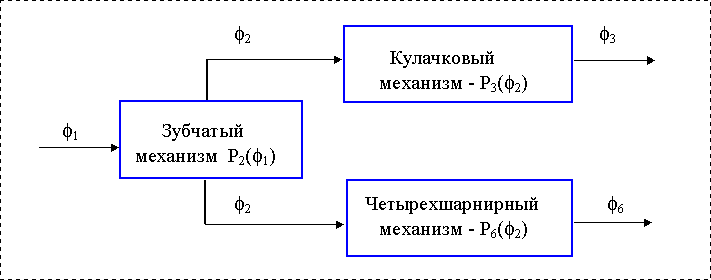
    Рассмотрим схему механической системы образованной последовательно-параллельным соединением типовых механизмов. Схема включает входное звено, зубчатую передачу , кулачковый и рычажный механизмы и имеет два выходных звена.

Схема механической системы

Рис. 3.2

Рис. 3.3

Функции положения в механизмах

Рис. 3.4

Методы геометро-кинематического исследования механизмов

• планов положений, скоростей и ускорений,

• проекций векторного контура,

• кинематических диаграмм,

• центроид,

• преобразования координат,

• экспериментальный,

• другие.

Связь кинематических и передаточных функций

    Линейные скорости и ускорения

    V_L= dS_L / dt = (dS_L / d₁) * (d₁ / dt) = V_qL * ₁;

    a _L = d(V_ql * ₁) / dt = (dV_qL / d₁) * (d₁ / dt) * ₁ + V_ql * ₁ = a_qL * ₁² + V_qL * ₁;

    Угловые скорости и ускорения

    _i = d_i / dt = (d_i / d₁) * (d₁ / dt) = _qi * ₁;

    _i = d(_qi * ₁) / dt = (d_i / d₁) * (d₁ / dt) * ₁ + _qi * ₁ = _qi * ₁² + _qi * _i.

    Так как данные формулы получены как производные от скалярных величин, то при операциях с векторными величинами они применимы только для проекций этих величин на оси координат.

1. Метод проекций векторного контура. (Рычажные механизмы).

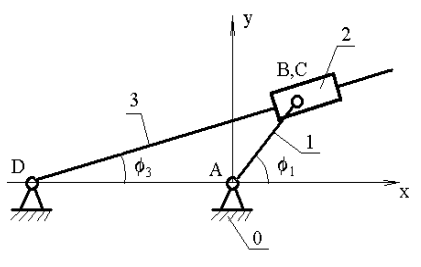
Рассмотрим простейший кулисный механизм.

Рис. 3.5

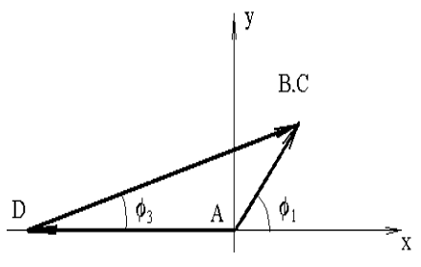
    Заменим кинематическую схему механизма эквивалентным векторным контуром

    Тогда уравнение замкнутости векторного контура запишется:

1. 1. Задача о положениях звеньев механизма

Рис. 3.6

    Проецируем векторный контур на оси координат и получаем координаты точки В механизма:

    x_B = l_AB * cos (₁) = l_AD * cos () + l_DB * cos (₃);

    y_B = l_AB * sin (₁) = l_AD * sin () + l_DB * sin (f₃);

из решения этой системы уравнений определяем неизвестные величины ₃ и l_DB, которые определяют положение звеньев и точек механизма

    tg (₃ ) = sin (₃) / cos (₃) = l_AB * sin (₁) / (l_AB * cos (₁) - l_AD * cos ());

    l_DB = (l_AB * sin (₁) / sin (₃);