1.3 Определение токов схемы методом наложения

По методу наложения ток в любом участке цепи рассматривается как алгебраическая сумма частных токов, созданных каждой ЭДС в отдельности.

Для начала преобразуем треугольник сопротивлений в звезду для удобства расчёта, (схема на рисунке 1.3').

Определяем частные токи от ЭДС 1 при отсутствии ЭДС 2 , то есть рассчитываем цепь по рисунку 1.3

Показываем направление частных токов от ЭДС Е₁ и обозначаем Решаем задачу методом "свертывания".

Рассчитываем эквивалентное сопротивление:

Рассчитываем токи во всех ветвях схемы:

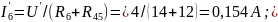
Определяем частные токи от ЭДС Е₂ при отсутствии ЭДС Е₁,то есть рассчитываем цепь по рисунку 1.4

Показываем направление частных токов от ЭДС Е₂ и обозначаем их

Рассчитываем эквивалентное сопротивление цепи:

Рассчитываем токи во всех ветвях схемы:

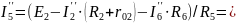
Вычисляем токи ветвей исходной цепи, (рисунок 1.1), выполняя алгебраическое сложение частных токов, учитывая их направление:

1.4 Составление баланса мощностей схемы

Источники , и вырабатывают электрическую энергию, так как направление ЭДС и тока в ветвях с источниками совпадают. Баланс мощностей для заданной цепи запишется так:

Мощность источников:

Мощность приёмников:

+

Баланс мощностей сошёлся.

Результаты расчетов токов по пунктам 1.2 и 1.3 представлены в виде таблицы 1.1.

Таблица 1.1 – Результаты расчётов

Ток в ветви Метод расчёта	А	А	А	А	А	А
Метод контурных токов				0,243
Метод наложения				0,243

Расчет токов ветвей обоими методами одинаков.

1.5 Определение тока во второй ветви методом эквивалентного генератора

Метод эквивалентного генератора используется для исследования работы какого-либо участка в сложной электрической цепи.

Найдём сопротивление, относительно зажимов

Пусть потенциал точки “0” равен 0. Тогда для нахождения надо найти потенциал точки “а”. Напишем уравнения узловых потенциалов для схемы:

Подставим значения и найдём потенциал “а”.

Потенциал .

Тогда ток равен:

.

1.6 Построение потенциальной диаграммы для контура, включающего обе эдс

Зная величину и направление токов ветвей и ЭДС, а также величины сопротивлений, вычислим потенциалы всех точек контура при переходе от элемента к элементу.

Строим потенциальную диаграмму. По оси абсцисс откладываем сопротивления контура в той последовательности, в которой производим обход контура, прикладывая сопротивления друг к другу, по оси ординат -потенциалы точек с учетом их знака. Потенциальная диаграмма представлена в Приложении А.