32

Лабораторная работа №16

Тема: Вычисление двойного интеграла в криволинейных координатах. Приложения двойных интегралов.

Задание 1: Найти площадь фигуры, ограниченной данными линиями.

Задание 2 Пластинка D задана ограничивающими ее кривыми, - поверхностная плотность. Найти массу пластинки.

Задание 3: Найти координаты центра масс однородных плоских фигур, ограниченных данными кривыми.

Для выполнения заданий используются исходные данные соответствующих таблиц 1 – 3, которые выбираются в соответствии с номером варианта.

ТАБЛИЦА 1

N
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.

ТАБЛИЦА 2

N	D
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.

ТАБЛИЦА 3

N		N
1.		13.
2.		14.
3.		15.
4.		16.
5.		17.
6.		18.
7.		19.
8.		20.
9.		21.
10.		22.
11.		23.
12.		24.

Теоретические положения

Замена переменных в двойных интегралах. Пусть функции

и (1)

осуществляют взаимно-однозначное непрерывно дифференцируемое отображение области Г плоскости Ouv на область G плоскости Oxy. Это означает, что в области G существует обратное непрерывно дифференцируемое отображение и и в области Г отличен от нуля якобиан преобразования, т.е.

(2)

Величины u и v можно рассматривать как прямоугольные координаты для точек области Г и в то же время как криволинейные координаты точек области G.

Если в двойном интеграле

произвести замену переменных по формулам (1), то областью интегрирования полученного интеграла будет уже область Г, которая при надлежащем выборе функций и может оказаться значительно проще области G, и имеет место формула

(3)

Для вычисления интеграла по области Г применяются изложенные в лабораторной работе №1 методы сведения двойного интеграла к повторным.

Наиболее употребительными из криволинейных координат являются полярные координаты

,

для которых

и формула (3) записывается в виде

. (4)

Приложения двойных интегралов.

Г е о м е т р и ч е с к и е п р и л о ж е н и я. Площадь S плоской области G выражается, в зависимости от рассматриваемой системы координат, следующими интегралами:

(5)

в декартовых прямоугольных координатах,

(6)

в криволинейных координатах. Здесь

в области Г.

В частности, в полярных координатах имеем

. (7)

Если гладкая поверхность имеет уравнение , то площадь части этой поверхности, проектирующейся в область g плоскости Oxy, равна

(8)

(функция однозначна в области G).

Объем V цилиндра, ограниченного сверху непрерывной поверхностью , снизу плоскостью z = 0 и с боков прямой цилиндрической поверхностью, вырезающей на плоскости Oxy область G, выражается интегралом

(9)

(функция однозначна в области G).

М е х а н и ч е с к и е п р и л о ж е н и я. Если пластинка занимает область G плоскости Oxy и имеет переменную поверхностную плотность , то масса М пластинки и ее статистические моменты M_x и M_y относительно осей Ox и Oy выражаются двойными интегралами

(10)

Координаты центра масс и пластинки определяются следующим образом:

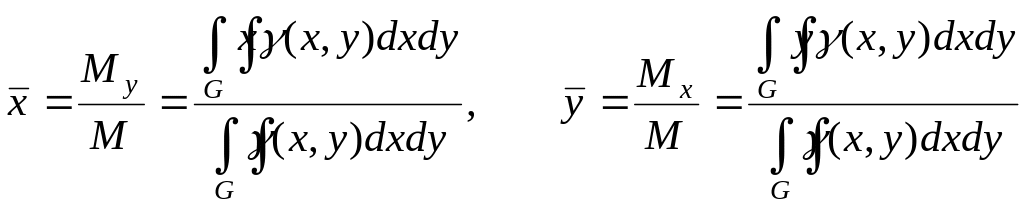(11)

Моменты инерции пластинки относительно осей Ox и Oy соответственно равны

(12)

а момент инерции пластинки относительно начала координат (полярный момент инерции) равен

(13)

Если пластина однородна, то в формулах (10)-(13) следует положить .

Пояснения и указания

к выполнению лабораторной работе №10

Задание 1: Найти площадь фигуры, ограниченной данными линиями.